Планирование и обработка результатов моделирования

Требуется оценить поведение объекта исследования (в данном случае целевой функции) в диапазонах изменении факторов Х₁: 5000 - 10000, Х₂: 2000 – 5000.

Применим для этого регрессионный анализ. Так как зависимость показателей эффективности от влияющих на них факторов неизвестна, то применим наиболее простые зависимости – полиномы первого и второго порядка.

Полином первого порядка для двух факторов имеет вид:

(1)

Полином второго порядка для двух факторов имеет вид:

(2)

Для вычисления коэффициентов полинома первого порядка (1) применяются планы полного факторного эксперимента (ПФЭ). Для двух факторов, представляемых в кодированном виде с изменением от -1 до +1, матрица планирования Х и матрица Y: центральная точка (первая строка) и ПФЭ (вторая – пятая строки) имеют следующий вид:

Номер плана	Х1	Х2	Y
1	0	0	Y0
2	-1	-1	Y1
3	1	-1	Y2
4	-1	1	Y3
5	1	1	Y4

Для нашей модели данная таблица будет иметь следующий вид:

Номер плана	X1	Х2	Y
1	7500	3500	314,96
2	5000	2000	314,54
3	10000	2000	310,16
4	5000	5000	309,52
5	10000	5000	310,16

Коэффициенты уравнения (1) определяются по формулам:

Тогда уравнение (1) будет иметь следующий вид:

(3)

По полученному аналитическому выражению можно сделать выводы:

1. Так как найденное значение коэффициента а₁ превышает значение коэффициента а₂, то фактор Х₁ (т.е. объём поставляемой партии) влияет на объект исследования сильнее, чем фактор Х₂ (величина запаса на складе). Кроме того, коэффициенты а₁, а₂ имеют отрицательное значение, т.е. оказывают отрицательное воздействие на прибыль Y.

2. Свободный член уравнения – коэффициент а₀ – величина достаточно большая, что может свидетельствовать о том, что в процессе моделирования были учтены не все факторы, влияющие на поведение объекта исследования (т.е. целевой функции) или изменение выделенных факторов производится в сравнительно небольших диапазонах.

3. Приближенное значение коэффициента а₁₂ к значениям коэффициентов при факторах говорит о том, что совместное влияние факторов существенно сказывается на прибыли.

Для получения полинома второго порядка применим ортогональный центральный композиционный план (ОЦКП). Для реализации ОЦКП к матрице планирования Х и к матрице Y добавляются ещё четыре «звёздные точки»:

Номер плана	Х1	Х2	Y
6	-1	0	Y5
7	1	0	Y6
8	0	-1	Y7
9	0	1	Y8

В нашем случае эта таблица имеет вид:

Номер плана	X1	Х2	Y
6	5000	3500	314,54
7	10000	3500	310,16
8	7500	2000	314,96
9	7500	5000	307,44

Коэффициенты уравнения (2) вычисляются по формулам:

(4)

Итак, уравнение (2) с учетом найденных коэффициентов имеет вид:

(5)

Полином второго порядка можно использовать для оптимизации. Для этого требуется найти частные производные полинома, приравнять их к нулю и решить получившуюся систему уравнений. Результатом решения будет точка, соответствующая оптимальным значениям факторов.

Найдём частные производные:

Решая полученную систему линейных уравнений, получаем значения величин х₁ и х₂, которые будут являться абсциссой и ординатой точки, соответствующей оптимальным значениям факторов для проведения эксперимента.

Оценим полученные экстремальные значения на наличие max и min.

Так как и А < 0, значит в точке (-1,32;-0,9) есть экстремум (максимум). Полученная точка имеет координаты, выходящие за пределы допустимой области. Поэтому, выполнив оптимизацию с помощью пакета «Поиск решения» в Microsoft Excel, получим такой же результат.

x1	x2	y
-1	-0,8	313,5784

Итак, точка (-1;-0,8) соответствует оптимальным значениям факторов для проведения эксперимента. Изобразим на координатной плоскости точку с координатами (х₁; х₂), которую условно обозначим за А. (Рис.1)

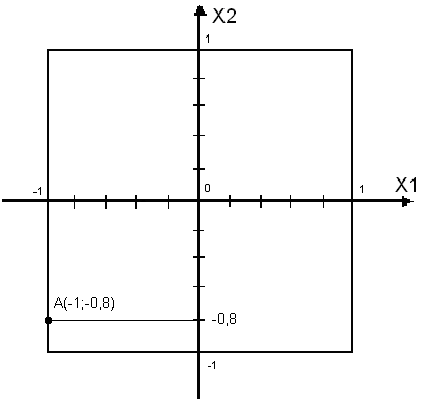
Рис. 1

По графику несложно заметить, что точка А с координатами (-1;-0,8) в кодированном виде будет соответствовать точке (5000; 2300) с оптимальными значениями параметров х₁ и х₂ соответственно.