- •Teil 4: Signalaufbereitung
- •5. Brückenschaltungen
- •5.1. Wheatstone-Brücke (1834)
- •5.1.1. Kompensationsmethode
- •5.1.2. Ausschlagmethode
- •Viertelbrücke
- •Vollbrücke, 4 aktive dms
- •Vollbrücke, 2 aktive, 2 quer dms (Nicht Linear)
- •Vollbrücke, 2 aktive, 2 quer dms (Linear)
- •4. Analoge Signalaufbereitung
- •4.1. Invertierender Verstärker
- •4.2. Nichtinvertierender Verstärker
- •4.3. Impedanzwandler
- •4.4. Strom-Spannungs-Wandler
- •4.5. Addierer/Summierverstärker
- •4.6. Differenzverstärker/Subtrahierverstärker
- •4.7. Integrator
- •4.8. Differentiator
- •5. Analog-Digitalwandlung
- •5.1. Grundlagen
- •5.1.1. Das Abtasttheorem
- •5.1.2. Sample and Hold Schaltung
- •5.1.3. Die Quantisierung
- •5.1.4. Die Codierung
- •5.2. Beispiele
- •5.2.1. Single Slope-Verfahren
- •5.2.2. Dual-Slope-Verfahren
- •5.2.3. Delta-Sigma-Verfahren
4.6. Differenzverstärker/Subtrahierverstärker
|
Hier wird der OPV so
beschaltet, dass er gleichzeitig als invertierender und
nichtinvertierender Verstärker arbeitet. Für den Betrieb als
invertierenden Verstärker wird der (+)-Eingang auf Masse gelegt,
dann gilt:
Für den
nichtinvertierenden Betrieb wird der (-)-Eingang auf Masse gelegt,
dann gilt:
Für die gesamte Schaltung gilt durch Überlagerung:
Sind speziell alle vier Widerstände gleich groß, so reduziert sich die Gleichung auf eine Subtraktion der Eingangsspannungen: Ua = Ue + − Ue − - Sind R1=R3 und R2=R4, so ist die Ausgangsspannung gleich der Differenz der Eingangsspannungen, multipliziert mit dem Faktor
R2
/ R1:
|
4.7. Integrator
|
Ein I. ist eine Schaltung mit frequenzabhängiger Gegenkopplung, meistens in Form eines Kondensators. Der Kondensator dient dabei als analoger „Speicher“ in dem die Eingangsspannung Ue über die Zeit aufaddiert wird. Bei konstanter Eingangsspannung ergibt sich eine linear ansteigende Ausgangsspannung. Integratoren sind in der analogen Schaltungstechnik Grundlage von Funktionsgeneratoren die beispielsweise Sägezahnschwingungen erzeugen. Genutzt wird der Integrator auch in der Regelungstechnik als Teilelement einer Regelstrecke bzw. eines Reglers. Der I. kann auch als aktiver Tiefpass betrachtet werden. Für die Ausgangspannung Ua als Funktion der Eingangsspannung Ue gilt:
Das dabei auftretende Produkt aus R und C nennt man Zeitkonstante, meist mit dem Zeichen τ abgekürzt. |
4.8. Differentiator
|
Beim D. werden frequenzabhängige Bauteile am Eingang der Schaltung verwendet. Fließt durch den Kondensator auf Grund von zeitlichen Änderungen der Eingangsspannung ein Lade-/ Entladestrom, bedingt dies einen Spannungsabfall am Widerstand und damit eine Änderung der Ausgangsspannung. Der D. wird in der Regelungstechnik eingesetzt, dann meistens in Kombination mit Proportionalverstärker und Integrator (PD- und PID-Regler). Der D. kann auch als Hochpass aufgefasst werden. Die Ausgangsspannung entspricht der links dargestellten Differentialgleichung mit der Zeitkonstanten τ = RC. |
5. Analog-Digitalwandlung
|
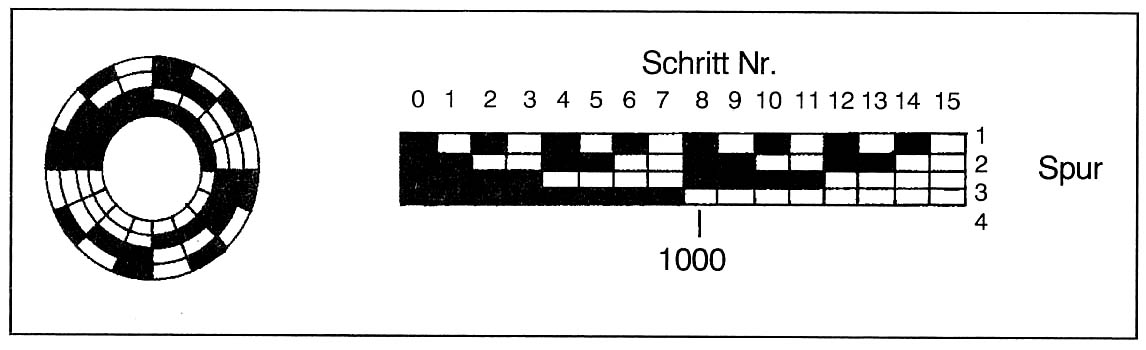
Prinzip der Analog-Digitalwandlung
1. Quantisierung Aufteilung eines analogen Wertebereichs (Ordinate) in 15 diskrete Werte, die in ein 4-Bit-Wort umgesetzt werden
2. Codierung Konvertierung der diskreten Analogwerte in ein binäres Wort |
|
Digitales Signal (4Bit-Winkelgeber)
In diesem Beispiel: Der Geber gibt die Zahlen von 0 bis 15
Abb. Kirbach |
5.1. Grundlagen
5.1.1. Das Abtasttheorem
Ein analoges Signal liegt zeitkontinuierlich vor . Um es in ein zeitdiskretes Signal zu überführen bedarf es einer mathematischen Grundlage (Nyquist, Raabe, Shannon). Unter zeitdiskreten Signalen, versteht man impulsförmige Signale, die nur während bestimmter (diskreter) Zeitwerte auftreten. Dem Abtasttheorem zufolge, lässt sich ein analoges Signal in eine Folge von zeitdiskreten Impulsen umwandeln, wenn man es in zeitlich gleichen Abständen (Abtastintervalle) durch Musterentnahme (Sampling) misst oder abtastet. Aus dem analogen Signal entsteht so ein pulsamplitudenmoduliertes (PAM-) Signal.
Shannon‘sches Theorem
Die Samplingfrequenz fS in der die Musterentnahme erfolgt, muss mindestens den doppelten Wert der höchsten im abzutastenden Signal enthaltenen Frequenz fm haben, d.h. : fS>= 2*fm .
Im Originalsignal darf keine Frequenz vorhanden sein, die größer ist als die Hälfte der Samplingfrequenz ist.
Bedeutung: Werden die Bedingungen des Shannon’schen Theorems erfüllt, findet die Umsetzung ohne Informationsverlust statt, obwohl alle Signaländerungen zwischen den einzelnen Samples keine Berücksichtigung finden. Die Rückwandlung in ein kontinuierliches Signal kann durch ein Tiefpassfilter, mit einer Grenzfrequenz die etwas größer ist als fmax geschehen. Der Abtastvorgang lässt sich nicht nur in der Zeitebene sondern auch in der Frequenzebene darstellen. Das analoge Signal mit dem zeitlichen Verlauf A=f(t) hat in der Frequenzebene eine maximale Nutzbandbreite fmax (a). Die Abtastung erfolgt in der Zeitebene mit periodischen Impulsen des Abstandes tS, die in der Frequenzebene die Spektren fS, 2fS,... aufweisen (b). Der Abtastvorgang entspricht einer Multiplikation von At mit St, die in der Frequenzebene Af*Sf dargestellt werden kann (c). Sie ergibt hier eine Wiederholung des Originalsignal-Spektrums mit dem Mehrfachen der Abtastfrequenz fS
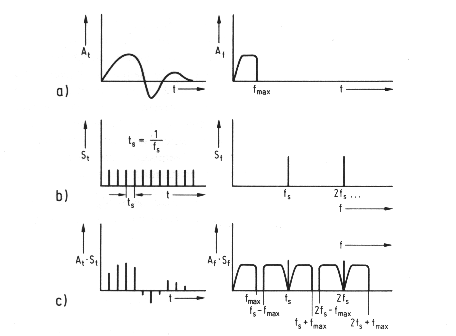 .
.
Wenn die zweite Bedingung, die besagt, dass fS immer größer sein muss als 2*fmax nicht eingehalten wird, so würde eine Überlappung des Original-Spektrums mit dem sich mit fS wiederholenden, modulierten Teil des Spektrums auftreten. Diese Überlappungen werden auch Aliasing-Komponenten, die harmonischen Verzerrungen als Aliasing- und Faltungsverzerrungen oder das ganze auch als Aliasing-Effekt bezeichnet. Auch eine Tiefpassfilterung kann diese Komponenten nicht mehr beseitigen. Der Aliasing-Effekt hat zur Folge, dass z.B. eine Frequenzkomponente von 39kHz in einem System mit einer Abtastfrequenz von 40kHz eine im Original nicht vorhandene, zusätzliche Frequenz von 1kHz erzeugen würde.

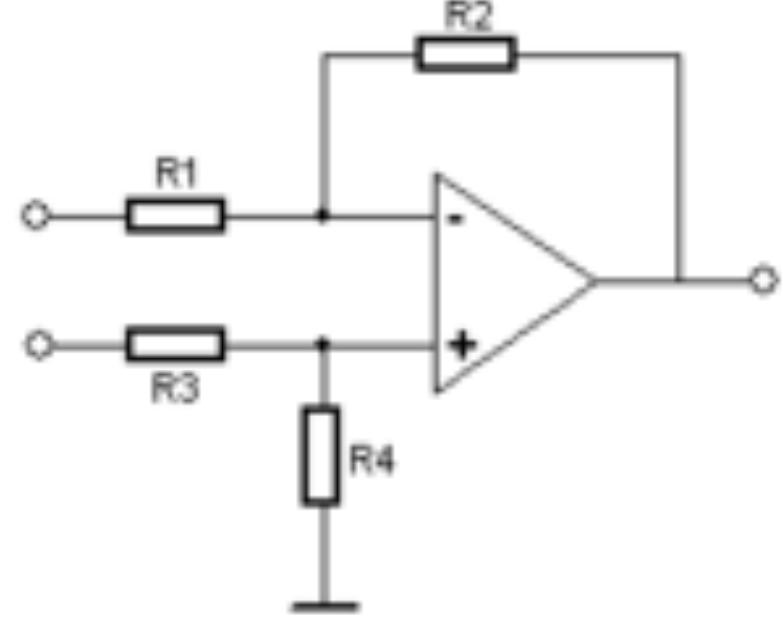
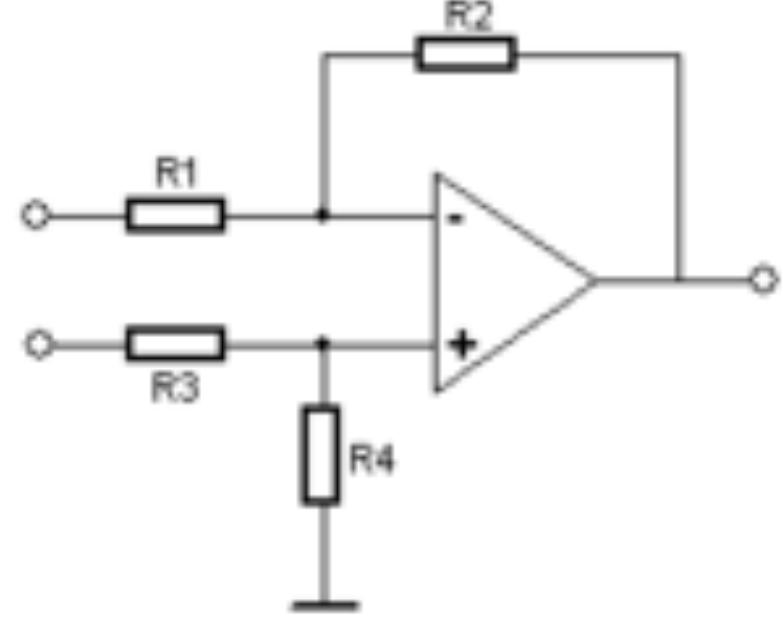
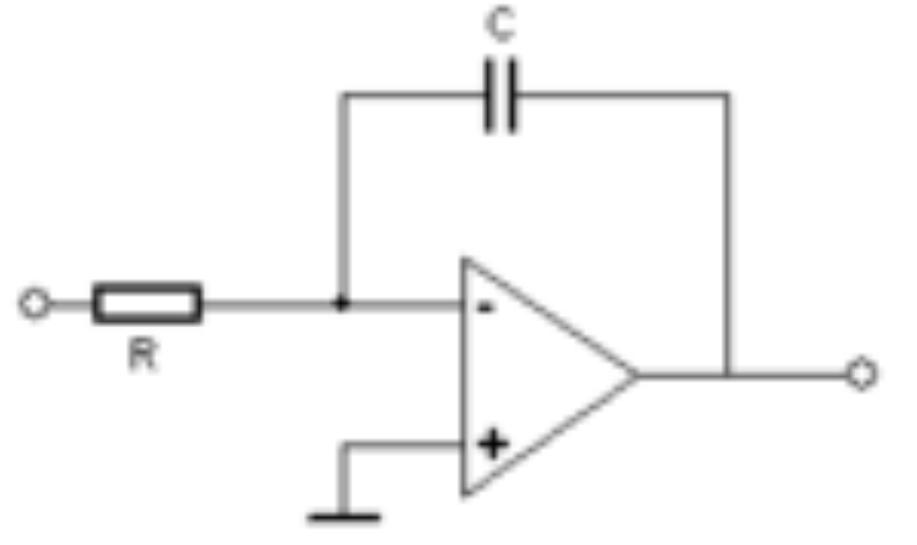
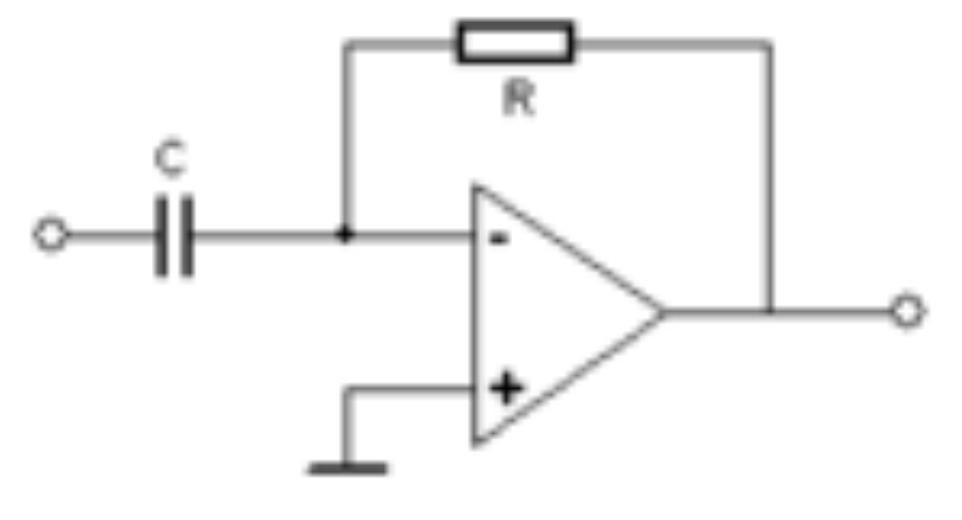
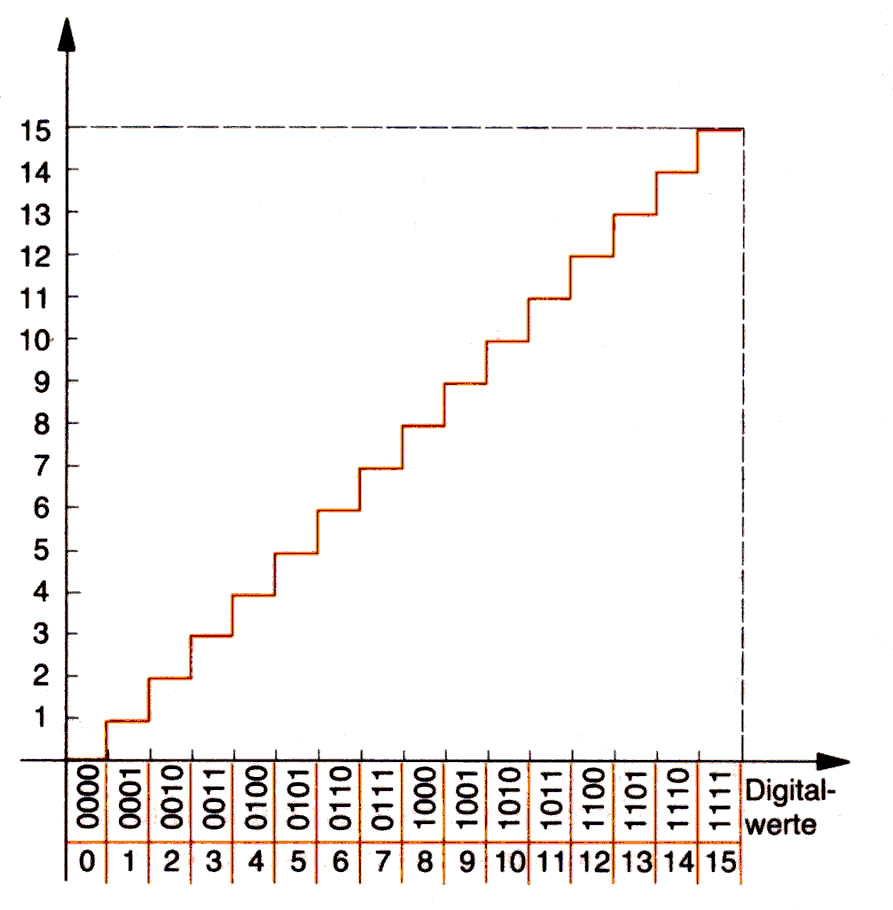 Abb. Beuth
Abb. Beuth