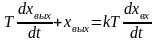- •Методы измерения влажности веществ.
- •Способы введения структурной избыточности устройств.
- •Вольт – амперные характеристики биполярных, моп- и кмоп- интегральных транзисторов.
- •Программные и следящие системы управления.
- •Операторная форма записи дифференциальных уравнений первого и второго порядков. Передаточные функции.
- •К омпенсационные измерительные схемы.
- •Аппаратурные средства для получения, передачи и обработки информации.
- •Микропроцессоры. Организация и структура микропроцессора.
- •Технологические процессы как объекты автоматического управления. Возмущения, управляющие воздействия, входы и выходы. Обобщенная, структурная схема.
- •Правила преобразования структурных схем управления. Связь между передаточными функциями разомкнутой и замкнутой систем.
- •Методы измерения расхода жидкостей.
- •Запоминающие устройства, элементы памяти на моп – интегральных транзисторах.
- •Оперативные запоминающие устройства
- •Постоянные запоминающие устройства
- •Сравнительные характеристики систем управления с жесткой и гибкой обратными связями.
- •Аналого-цифровые преобразователи. Структурные схемы ацп.
- •Цифровые преобразователи. Схема цифрового преобразователя.
- •Транзисторы. Типы. Характеристики.
- •Амплитудно-частотная (ачх), фазо-частотная (фчх) и амплитудо-фазо-частотная (афчх) характеристики.
- •Тензопреобразователи. Принцип действия и конструктивные формы.
- •Состав и особенности одноуровневых сапр
- •Критерий Рауса
- •Дифференциальное уравнение, передаточная функция, график переходной функции и частотные характеристики усилительного звена.
- •Нормирующие преобразователи и их характеристики.
- •Цифро-аналоговые преобразователи. Структурные схемы цап разных типов.
- •Сглаживающие фильтры. Стабилизаторы напряжения.
- •Чистое запаздывание. Передаточная функция звена чистого запаздывания. Графики его переходной функции и частотных характеристик.
- •Сельсинные преобразователи. Принцип действия. Применение в пищевой промышленности.
- •Особенности построения радиальных многоуровневых сапр
Операторная форма записи дифференциальных уравнений первого и второго порядков. Передаточные функции.
Дифференциальное уравнение, описывающее САУ, имеет вид: уравнение САУ:

Применив преобразование Лапласа, считая начальные условия нулевыми, получим
 ,
,
где
 - передаточная функция по каналу
управления,
- передаточная функция по каналу
управления,
 -
передаточная функция по каналу возмущения.
-
передаточная функция по каналу возмущения.
Передаточная функция системы – отношение изображения по Лапласу её выходного сигнала к изображению по Лапласу её входного сигнала при нулевых начальных условиях.
Выражение

является характеристическим многочленом системы.
Корни полинома знаменателя передаточной функции называются её полюсами, а корни полинома числителя – нулями.
Так как произвольный полином можно разложить на простые множители, то передаточную функцию системы (звена)

всегда можно представить в виде произведения простых множителей и дробей вида
k,
s,
 ,
,
 (1.4)
(1.4)
Звенья, описываемые дифференциальными уравнениями 1 и 2 порядка, называют элементарными, или типовыми.
Здесь к называется передаточным коэффициентом, Т — постоянной времени и (0 < < 1) — коэффициентом демпфирования.
Звено с передаточной функцией W(s) = к называется пропорциональным звеном, звено с передаточной функцией W(s) — ks — дифференцирующим звеном, звено с передаточной функцией \Y(s) = = k/s — интегрирующим звеном, звено с передаточной функцией W(s) = k(Ts+ l) — форсирующим звеном (первого порядка), звено с передаточной функцией W(s) = k/(Ts+ l) — апериодическим звеном, звено с передаточной функцией
 (0
< ϛ
< 1- колебательным
звеном, ϛ
> 1 апериодическим
звеном 2 порядка)
(0
< ϛ
< 1- колебательным
звеном, ϛ
> 1 апериодическим
звеном 2 порядка)
Существуют также звенья, которые не являются в полном смысле элементарными, но их относят к числу типовых:
Реальное дифференцирующее звено, реальное интегрирующее звено, консервативное звено, форсирующее звено 2 порядка.
В таблице приведены дифференциальные уравнения объедков управления 1,2 порядка.
Характеристика объекта могут быть получены экспериментальным путем (переходная, весовая функция, частотные характеристики). В таблице показана также связь параметров передаточной функции, получаемой из диф. уравнения, с видом переходной функции ОУ.
При этом следует учитывать, что временные характеристики интегрирующих и дифференцирующих звеньев практически не применяются.
Звено |
Уравнение звена |
Передаточная функция |
|
Усилительное |
|
|
|
Интегрирующее |
|
|
|
Апериодическое |
|
|
|
Колебательное |
|
|
|
Дифференцирующее идеальное |
|
|
|
Дифференцирующее реальное |
|
|
|
Запаздывающее |
|
|
|
К омпенсационные измерительные схемы.
Принцип действия компенсатора основан на уравновешивании (компенсации) измеряемого напряжения известным падением напряжения на образцовом резисторе. Момент полной компенсации фиксируется по показаниям индикаторного прибора (нуль-индикатор).
Упрощенная
схема компенсатора постоянного тока
приведена на следующем рисунке. Схема
содержит источник образцовой ЭДС
 ,
образцовый резистор
,
образцовый резистор
 ,
вспомогательный источник питания
,
вспомогательный источник питания
 ,
переменное (компенсационное) сопротивление
,
переменное (компенсационное) сопротивление
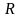 ,
регулировочный реостат
,
регулировочный реостат
 и нуль-индикатор
и нуль-индикатор
 .
Нуль-индикатором служит обычно
гальванометр с нулем посредине шкалы.
В качестве образцовой ЭДС используется
нормальный элемент – изготавливаемый
по специальной технологии гальванический
элемент, среднее значение э.д.с. которого
при температуре 20 оС
известно и равно
.
Нуль-индикатором служит обычно
гальванометр с нулем посредине шкалы.
В качестве образцовой ЭДС используется
нормальный элемент – изготавливаемый
по специальной технологии гальванический
элемент, среднее значение э.д.с. которого
при температуре 20 оС
известно и равно
 В. Процесс измерения напряжения состоит
из двух операций: установления рабочего
тока и уравновешивания измеряемого
напряжения. Для установления рабочего
тока переключатель П ставят в положение
1 и, регулируя сопротивление
,
добиваются отсутствия тока в гальванометре.
Это будет иметь место в том случае, когда
падение напряжения на резисторе
В. Процесс измерения напряжения состоит
из двух операций: установления рабочего
тока и уравновешивания измеряемого
напряжения. Для установления рабочего
тока переключатель П ставят в положение
1 и, регулируя сопротивление
,
добиваются отсутствия тока в гальванометре.
Это будет иметь место в том случае, когда
падение напряжения на резисторе
 станет равным ЭДС нормального элемента:
станет равным ЭДС нормального элемента: .
.
При
этом рабочий ток в цепи

 .
.
После
установки рабочего тока переключатель
П устанавливают в положение 2 и, не
изменяя рабочего тока, устанавливают
такое значение сопротивления
 ,
при котором измеряемое напряжение
,
при котором измеряемое напряжение
 будет уравновешено падением напряжения
будет уравновешено падением напряжения
 и ток в цепи гальванометра снова будет
отсутствовать. Отсюда
и ток в цепи гальванометра снова будет
отсутствовать. Отсюда
 и
и
 .
.
Одно из основных достоинств компенсаторов – отсутствие потребления мощности от объекта измерения, т.е. возможность измерения ЭДС.
Погрешность
компенсатора определяется погрешностями
резисторов
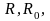 ЭДС нормального элемента, а также
чувствительностью индикатора. Современные
потенциометры постоянного тока
выпускаются классов точности от 0,0005 до
0,2.
ЭДС нормального элемента, а также
чувствительностью индикатора. Современные
потенциометры постоянного тока
выпускаются классов точности от 0,0005 до
0,2.
В
современных конструкциях компенсаторов
вместо нормального элемента используются
стабилизированные источники напряжения
с более высоким значением
 ,
что позволяет расширить верхний предел
измерения компенсатора до нескольких
десятков вольт.
,
что позволяет расширить верхний предел
измерения компенсатора до нескольких
десятков вольт.
Компенсационные методы используются также для измерения на переменном токе.




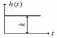




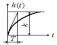
 при
при