3.4. Характеристика рядів розподілу Ряди розподілу характеризуються коефіцієнтом асиметрії та коефіцієнтом ексцесу.

Коефіцієнт асиметрії показує скошеність кривої нормального закону розподілу вправо чи вліво відносно осі ОХ.

де ‑ середнє значення ознаки;

М_О – модальне значення ознаки;

 ‑ середньоквадратичне відхилення.

Якщо А0, то скошеність буде лівостороння.

Якщо А0, то скошеність буде правосторонньою.

Якщо А=0 – розподіл симетричний.

Для нормального розподілу характерним є те, що середня арифметична, мода і медіана рівні між собою. Для асиметричного розподілу характерні деякі розбіжності:

• при правосторонній асиметрії >Mе>Mo

• при лівосторонній асиметрії < Mе<Mo

Коефіцієнт ексцесу характеризує гостровершність вершини розподілу, скупченість варіантів навколо середньої арифметичної.

де  ‑ середньоквадратичне відхилення;

 ‑ центральний момент розподілу.

де ‑ середнє значення ознаки;

Xi – індивідуальне значення ознаки;

- загальна сума частот усіх інтервалів.

Якщо Е3, то вершина кривої розподілу – гостроверха.

Якщо Е3 – нормальна крива.

Якщо Е3 ‑ вершина кривої розподілу – тупа вершина.

Розрахунки:

• кількісна ознака час простою:

- тобто крива розподілу часу простою скошена вправо відносно кривої нормального розподілу (А>0).

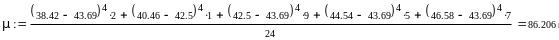
σ ⁴ = 5,6²=31,36

< 3, вершина тупа.

• кількісна ознака виручка:

- крива розподілу для виручки скошена вліво відносно кривої нормального розподілу (А<0).

σ ⁴ =_227142,79²=51593847048,98

< 3, вершина тупа.

3.5. Перенос результатів вибіркового спостереження на генеральну сукупність.

До цієї частини курсової роботи ми мали справу лише з вибірковим спостереженням. Чому ми використовували вибіркове спостереження:

• економія часу;

• зведення до мінімуму порчі одиниць сукупності;

• необхідність детального вивчення кожної одиниці сукупності;

• правильний розрахунок помилок реєстрації.

До задач вибіркового спостереження належать:

• визначення помилки репрезентативності;

• визначення об’єму вибірки, що необхідна для даної ознаки.

Для випадкового без повторного відбору середня помилка репрезентативності становить:

де ² – дисперсія, квадрат середньоквадратичного відхилення;

n – кількість одиниці вибіркової сукупності;

N ‑ кількість одиниці генеральної сукупності.

Гранична помилка репрезентативності, яка залежить від коефіцієнту довіри t:

_х = t×_х,

де t = 1, t = 2, t = 3, що відповідає вірогідності р = 0,683, р = 0,954, р = 0,997 відповідно.

Розповсюдження результатів безповторного вибіркового спостереження на генеральну сукупність здійснюється методом прямого перерахування, коли узагальнюючий показник вибіркової сукупності множиться на кількість одиниць генеральної сукупності.

Для кількісної ознаки – час простою за 10 днів, середня помилка репрезентативності становить:

Гранична помилка репрезентативності при заданому коефіцієнті довіри t=2, з ймовірністю 0,954:

_х = 2×0,45 = 0,9

Тобто, враховуючи заданий рівень вірогідності, можна сказати, що із генеральної сукупності 184 водіїв в 24 індивідуальна кількість їздок буде змінюватися в межах:

42,79  44,59

Для кількісної ознаки – час простою за 10 днів, середня помилка репрезентативності становить:

Гранична помилка репрезентативності при заданому коефіцієнті довіри t=2, з ймовірністю 0,954:

_х = 2×210,859=421,7

Отже, враховуючи заданий рівень вірогідності, можна сказати, що із генеральної сукупності 184 водіїв індивідуальні значення виручки буде змінюватися в межах:

614,86  1458,26