Вариант №5

Задача 1. Функция спроса задана таблично. Найти эластичность спроса в каждой точке и на отрезках между ними.

Q, шт 6 8 10

P, руб. 12 6 4

Задача 2. Дана бюджетная линия потребителя с доходом 500 ед.

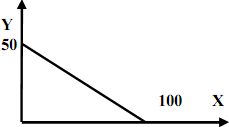Найти уравнение бюджетной линии.

Задача 3. Фермер выращивает две культуры — саго (X) и фасоль (Y) — на двух полях. Уравнения кривых производственных возможностей на этих полях имеют следующий вид: первое поле: ; второе поле: .

а) Пусть фермер производит 15 единиц саго и 10 единиц фасоли на первом поле, а также 20 единиц саго и 10 единиц фасоли на втором поле. Использует ли фермер свои ресурсы эффективно? Обоснуйте свой ответ.

б) В новом сезоне фермер решил пересмотреть решение о производстве. На первом поле он попрежнему вырастил 15 единиц саго и 10 единиц фасоли. Второе же поле он засеял по-другому: теперь урожай этого поля составил 18 единиц саго и 18 единиц фасоли. Использует ли фермер свои ресурсы эффективно в новой ситуации? Обоснуйте свой ответ.

Задача 4. Студент, ведущий здоровый образ жизни, считает, что ему одинаково полезно еженедельно выпивать как 8 стаканов молока и три стакана кефира, так и 6 стаканов молока и 4 стакана кефира. Чему в этом случае равна его предельная норма замещения кефира на молоко?

Задачи:

5. Производственная функция фирмы имеет вид: Q = 50 .

1. Каким будет максимальный выпуск фирмы, если ТС = 400, P = 5, P = 20?

2. Как изменится выпуск фирмы, если цена труда возрастет до 20 ден.ед.? Найдите эффект замены и эффект выпуска в общем изменении спроса на труд.

6. Функция общих затрат фирмы имеет вид: TC = 30000 + 50Q. Цена на ее продукцию меняется по формуле: P =100 – 0,01Q.

а) Определить цену, при которой фирма получит максимум прибыли, и размер этой прибыли.

б) Определить те же параметры, если фирма должна будет уплачивать налог в размере 10 ден. ед. с каждой реализованной единицы продукции.

в) Определить те же параметры, если фирма должна уплачивать налог на капитал в размере 200 ден. ед.

7. Функция общих затрат фирмы имеет вид ТС= 400 Q - 4 Q² + 0,2 Q³. Определить величину предельных затрат фирмы при Q = 6.

Вариант №6

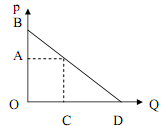
Задача 1. Дана функция спроса на графике. Р_А = [ОА], Рмах = [ОВ]. Доказать, что эластичность в точке Р_А : Еd( Р_А) = [ОА]/[АВ].

Задача 2. Предельная полезность X для индивида отображается функцией MU_Х = 40 – 5Х, а предельная полезность Y, MU_Y = 20 – 3Y. Известны цены благ и доход индивида: P_Х = 5; P_Y = 1; I = 20. Какое количество каждого из благ должен купить индивид для максимизации общей полезности?

Задача 3. Спрос и предложение на рынке бензина в городе N задаются линейными функциями. Этот рынок первоначально находился в состоянии конкурентного равновесия. Городские власти приняли решение субсидировать цены на бензин: субсидия была установлена в размере 10 рублей на литр бензина. В результате субсидирования установилось новое конкурентное равновесие. По сравнению с первоначальным равновесием, цена, которую покупатель платит за литр бензина, сократилась с 36 до 32 рублей, а общий рыночный объем продаж бензина вырос с 7 тысяч литров до 9 тысяч литров.

1) На какую величину увеличился излишек потребителей в результате введения субсидии?

На какую величину увеличился излишек производителей в результате введения субсидии?

Кто получил больший выигрыш от субсидирования – потребители или производители?

2) Какая величина больше: суммарное изменение излишков производителей и потребителей от субсидирования или расходы властей на субсидирование?

Задача 4. Дана бюджетная линия потребителя. Цена товара Y – 50.

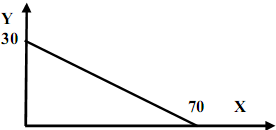Каков доход потребителя?

Задачи:

5. Отраслевой спрос на продукцию характеризуется функцией: Q = 300 – 18P. При существующей технологии и заданных ценах на факторы производства функция общих затрат фирмы, производящей данную продукцию, имеет вид: TC = q - 20q + 160.

а) По какой цене и сколько единиц продукции будет продано в краткосрочном периоде каждой фирмой и на рынке в целом, если в отрасли будет работать 20 таких фирм?

б) Сколько таких фирм будет в отрасли в долгосрочном периоде?

в) Покажите решение графически.

6. Заполните таблицу, где приведены данные о результатах деятельности предприятия.

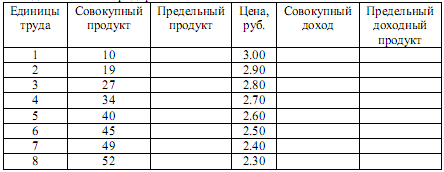
7. Производственная функция фирмы: q=2K^0,6L^0,4. За долгосрочный период фирма расширилась, удвоив затраты труда и капитала. Во сколько раз возрастет выпуск фирмы? Как при этом изменится средний продукт труда и капитала? Обоснуйте ответы, опираясь на отдачу от масштаба при данной производственной функции.