Розділ 2. Диференціальне числення функції однієї змінної

Тема 2.1. Диференційовність функції однієї змінної

Мета. Розширити поняття диференційовності функції однієї змінної, дати поняття диференціала та його зв’язку з похідною. Ознайомитись з методами та способами знаходження похідних основних класів функцій.

План.

1. Похідна функції, її зміст в різних задачах.

2. Необхідна умова диференційовності.

3. Основні правила диференціювання.

4. Похідні елементарних функцій.

5. Метод логарифмічного диференціювання.

6. Диференціал першого порядку, його геометричний та механічний зміст.

1. Розглянемо наступні задачі

а) Нехай дано криву АВ і точку М₀ , яка цій кривій належить. Візьмемо довільну точку М цієї ж кривої і проведемо пряму ММ₀. Пряма, що проходить через дві точки кривої називається січною. Січна з кривою можуть мати дві або більше спільних точок. Нехай точка М рухається вздовж кривої до точки М₀, тоді січна рухається до якогось свого граничного положення М₀Т і така пряма, яка є граничним положенням називається дотичною.

Означення: Дотичною до кривої L в точці М₀ називається граничне положення січної ММ₀, якщо точка М прямує до точки М₀ вздовж кривої.

Дотична з кривою мають одну спільну точку в деякому околі.

О бчислимо кутовий коефіцієнт дотичної до графіка функції y=f(x).

k=tg a, де a– кут нахилу дотичної до осі Ох.

Тоді tg= , але при М®М₀ справедливо Dх®0, а сам кутовий коефіцієнт логічно шукати як

k= = .

б) Нехай деяке тіло рухається прямолінійно за заданим законом s=f(t). Тоді за час Dt тіло пройшло відстань Ds, а – середня швидкість тіла на цьому проміжку.

Означення: Швидкістю тіла в кожен конкретний момент часу t називають границю середньої швидкості тіла на цьому проміжку, при умові, що Dt прямує до 0. Тобто .

в) Розглянемо задачу про обчислення сили змінного струму.

Нехай Q=f(t) – кількість електрики, що проходить за час t. Сила струму – це кількість електрики, що проходить через поперечний переріз за час t. За проміжок часу Dt пройде DQ струму. – середня сила струму за час Dt. А в кожен конкретний момент .

Ці всі задачі приводять нас до необхідності обрахування границі відношення приросту функції до приросту аргумента, якщо приріст аргумента прямує до нуля.

Нехай функція y=f(x) визначена в точці х₀. Надамо їй приросту так, щоб х₀+Dх належала області визначення і знайдемо приріст функції в цій точці. Dy=f(x₀+Dx) – f(x₀).

Похідною функції f(x) в точці х₀ називається границя відношення приросту функції Dy до приросту аргументу Dх , якщо приріст аргумента прямує до нуля довільним способом.

Позначають .

Або .

Існують також позначення , .

Фізичним змістом похідної є розв’язок задачі про швидкість тіла (позначають .

Геометричним змістом похідної є розв’язок задачі про знаходження кутового коефіцієнта дотичної до кривої (позначаємо .

2. Означення 1. Функція f(x) називається диференційованою в точці х₀, якщо вона має похідну в цій точці.

Означення 2. Функція f(x) називається диференційованою в деякому інтервалі, якщо вона має похідну в кожній точці цього інтервалу.

Теорема (необхідна ознака диференційовності функції): Якщо функція y=f(x) диференційовна в точці х, то вона неперервна в цій точці.

Доведення.

Нехай в точці х існує похідна

.

Звідси і з рівності

за теоермою про границю добутку маємо

.

А це означає, що функція f(x) в точці х неперервна.

Теорему доведено.

Обернена теорема взагалі кажучи не справджується. Тобто існують неперервні функції, які в окремих точках не мають похідних. Прикладом такої функції може бути .

3. Теорема 1. Якщо функції f(x) і j(х) диференційовані в точці х, то в цій точці диференційована функція f(x) + j(х), причому

,

тобто похідна суми диференційованих в точці х функцій дорівнює сумі похідних цих функцій в розглядуваній точці.

Доведення.

Позначимо F(x)=f(x)+j(x) і отримаємо

DF(x)=(f(x+Dх)+j(x+Dх)) – (f(x)+j(x))

Звідси .

Якщо умови теореми виконанні, то і . (*) Використовуючи теорему про границю суми отримаємо

.

Тобто, функція F(x) диференційована і теорема має місце.

Теорема 2. Якщо функції f(x) і j(х) диференційовані в точці х, то в цій точці диференційована функція f(x)j(х), причому

,

тобто похідна добутку диференційованих в точці х функцій дорівнює сумі похідної першої з цих функцій в розглядуваній точці на другу функцію без зміни плюс похідну другої з цих функцій в розглядуваній точці на першу функцію без зміни .

Доведення.

Позначимо F(x)=f(x)j(x) і отримаємо

DF(x)=(f(x+Dх)j(x+Dх)­)–(f(x)j(x))=

+ = ,

Звідси .

Якщо умови теореми виконані, то і .

Крім того, внаслідок теореми про неперервність диференційованої функції

.

Використовуючи теорему про границю добутку отримаємо

Тобто функція F(x) диференційована і теорема є справедливою.

Лема. Якщо f(x)=c, де с – стала для хÎ(a, b), то , тобто похідна сталої функції дорівнює нулю.

Доведення.

Маємо

,

звідси

Наслідок 1. Якщо функція f(x) диференційована в точці х, то функція cf(x), де с– стале число є диференційованою , причому

,

тобто сталий множник можна винести за знак похідною.

Доведення випливає з теореми 2 і леми.

Наслідок 2.Різниця двох функцій, диференційованих в точці х є функція, диференційована у точці х, причому

.

Доведення випливає з наслідку 1 і теореми 2.

Теорема 3. Якщо функції f(x) і j(х) диференційовані в точці х, причому в цій точці j(х)¹0, то в цій точці диференційована функція f(x)/j(х), причому

.

Доведення. Цілком аналогічне доведенню теорем 1 та 2.

Наслідок 3. Якщо функція j(х) диференційована в точці х, причому в цій точці j(х)¹0, то в цій точці диференційована функція , причому

.

4.Теорема. Справедливі наступні рівності:

Доведення: Рівність 1) доведено в попередній темі.

Доведемо рівність 2):

Якщо n-натуральне число (n>1), то для будь-якого х 

У точці х0, яка є внутрішньою точкою області існування функції х^(–дійсне число), маємо

Якщо х=0; >1, y(x)=x^, то

Отже, формула 3) справедлива для кожної внутрішньої точки області існування функції y=x^ за винятком точки х=0, коли >1.

Формули 4) і 5) випливають з формули 3) при =1 / 2 та =-1.

Якщо a>0, то а1, то, використовуючи рівність маємо

Зокрема,

Використовуючи першу чудову границю і неперервність функції cos x для довільного х( знайдемо

Аналогічно доводимо формулу

Використовуючи теорему про похідну частки і вищенаведені рівності, маємо

Аналогічно доводимо, що

Використовуючи рівність

,

маємо

Зокрема,

5. Якщо потрібно продиференціювати функцію , задану у вигляді дробу, добутку чи у вигляді степеневої функції, основою і показником якої є функції незалежного аргументу вигідно спочатку прологарифмувати обидві частини функції за основою е, а вже потім диференціювати. Цей прийом має назву логарифмічного диференціювання. Похідна від логарифму називається логарифмічною похідною. До цього засобу зручно звертатися і тоді, коли ми маємо функцію, що містить корені з дробів. І до нього завжди звертаються, коли необхідно продиференціювати функцію вигляду

Розглянемо цей спосіб на прикладі:

Знайти похідну функції .

Розв’язування:

Прологарифмуємо обидві чатини рівності

.

Вважаючи, що ln y є складеною функцією від х і диференціюючи обидві частини рівності , маємо

.

Множимо обидві частини рівності на , отримуємо, що шукана похідна має вигляд

.

Після очевидних спрощень отримаємо: .

6. Означення диференційовної функції можна дати і не використовуючи поняття похідної.

Означення: Функцію f(x) назвемо диференційовною в точці х, якщо приріст цієї функції в точці х можна зобразити у вигляді:

, де і число А не залежить від . (1)

Покажемо, що попереднє означення рівносильне щойно даному. Справді, якщо функція f(x) диференційовна в точці х за поперднім означенням, то ця функція має в точці х похідну. Позначивши , дістанемо , де границя =0, тобто функція f(x) диференційовна за новим означенням. Роль числа А тут виконує . Можна показати, що обернене твердження також справедливе, тобто, якщо функція диференційовна в новому змісті, то вона диференційована і в старому смислі . Таким чином, якщо функція диференційована в точці х, то її можна записати у вигляді (1).

Приріст складається з двох доданків і При фіксованому

Х обидва доданки є нескінченно малими функціями при прямуючому до 0.

Одначе ці нескінченно малі функції мають різний порядок ніж

є нескінченно малою функцією вищого порядку ніж

Іншими словами перший доданок незмірно великий в порівнянні з другим. Це дає змогу вважати перший доданок головною частиною приросту функції. Ця головна частина є лінійною відносно .

Означення: Лінійна відносно х частина приросту диференційовної функції в точці х називається диференціалом цієї функції в цій точці і позначається

Д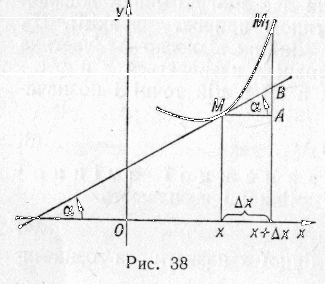 иференціал незалежної змінної х позначають dx=x. Отже, формулу диференціалу можна записати і у вигляді

Нехай функція f(x) диференційовна в точці х.

Тоді в точці (x, f(x)) графік функції має дотичну, нахилену до осі абсцис під кутом ,

З малюнка видно, що

АВ=МА .

Тобто, диференціал функції в точці х дорівнює приросту ординати дотичної до кривої y=f(x) в точці х, коли незалежна змінна х дістає приріст х.

Слід відмітити, що диференціал функції може бути і більшим, і меншим, і рівним приросту.