2. Задачи повышенного уровня сложности

1. Вычисление криволинейных интегралов.

7.36. Вычислить интеграл , где - первая арка циклоиды .

7.37. Вычислить интеграл , где - дуга развертки окружности .

7.38. Вычислить интеграл 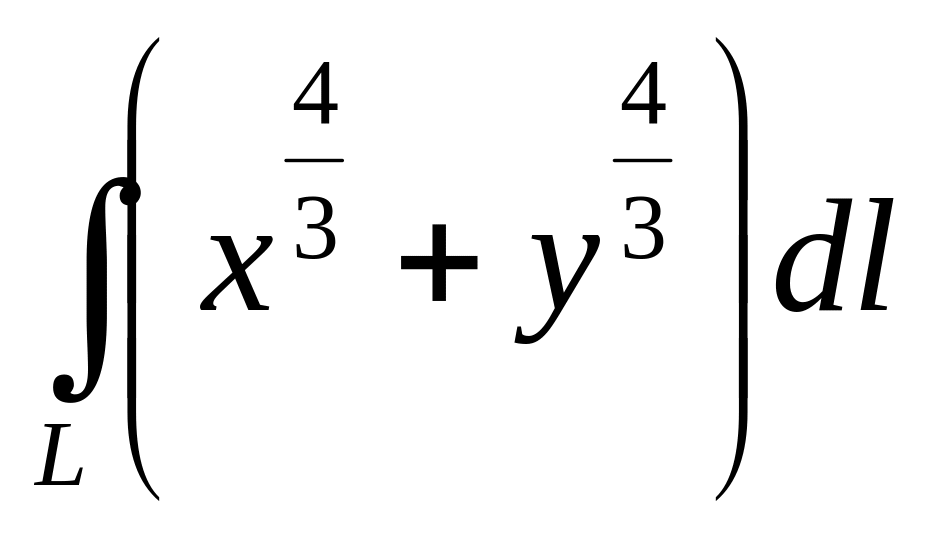, где кривая - астроида ( ).

7.39. Вычислить , где - часть спирали Архимеда , заключенная внутри круга радиуса с центром в начале координат.

2. Вычисление длины кривой.

7.40. Найти длину дуги конической винтовой линии от точки до точки .

7.41. Вычислить периметр треугольника, вершинами которого являются точки .

7.42. Вычислить длину замкнутой кривой, представляющую собой эллипс .

3. Вычисление площади боковой поверхности.

7.43. Вычислить площадь цилиндрической поверхности, ограниченной снизу плоскостью , сверху поверхностью , при условии, что направляющая кривая - четверть эллипса , лежащая в первой четверти .

7.44. Вычислить площадь цилиндрической поверхности, ограниченной снизу плоскостью , сверху поверхностью , при условии, что направляющая кривая - арка циклоиды .

7.45. Найти площадь боковой поверхности параболического цилиндра , ограниченной плоскостями .

4. Вычисление массы материальной кривой.

7.46. Найти массу четверти эллипса , расположенной в первой четверти, если линейная плотность в каждой точке пропорциональна ординате этой точки.

7.47. Вычислить массу однородной дуги циклоиды .

7.48. Найти массу первого витка винтовой линии , если ее плотность в каждой точке равна расстоянию этой точки до начала координат.

7.49. Вычислить массу эллипса , если его линейная плотность равна .

5. Вычисление координат центра тяжести кривой.

7.50. Вычислить координаты центра тяжести однородной дуги циклоиды .

7.51. Вычислить координаты центра тяжести однородной материальной кривой от точки до точки .

7.52. Вычислить координаты центра тяжести контура однородного сферического треугольника .

7.53. Найти статические моменты дуги астроиды ( ), , относительно осей координат, если ее линейная плотность равна единице.

6. Вычисление моментов инерции материальной кривой.

7.54. Найти момент инерции относительно оси первого витка винтовой линии .

7.55. Найти момент инерции относительно оси дуги циклоиды .

7. Разные задачи.

7.56. Вычислить проекции на оси координат силы, с которой материальная однородная полуокружность , массы притягивает материальную точку массы .

7.57. Найти силу, с которой ток в бесконечном прямолинейном проводнике действует на точечный магнитный заряд , находящийся на расстоянии от проводника.

Указание. При вычислении использовать закон Био-Савара: элемент тока действует на точечный магнитный заряд с силой, равной по величине , где - ток, - элемент длины проводника, - расстояние от элемента тока до магнитного заряда, - угол между направлением прямой, соединяющий магнитный заряд и элемент тока, и направлением самого элемента тока. Эта сила направлена по нормали к плоскости, соединяющей элемент тока и точку, в которой помещен магнитный заряд: направление силы устанавливается правилом «буравчика».

7.58. По контуру, имеющему форму квадрата со стороной , течет ток . С какой силой этот ток действует на точечный магнитный заряд , находящийся в центре квадрата?

7.59. С какой силой ток , текущий по замкнутому эллиптическому контуру, действует на точечный магнитный заряд , находящийся в фокусе эллипса?

7.60. С какой силой ток , текущий по бесконечному параболическому контуру, действует на точечный магнитный заряд , помещенный в фокусе параболы? Расстояние от вершины до фокуса равно .

7.61. С какой силой ток , текущий по круговому контуру радиуса , действует на точечный магнитный заряд , помещенный в точку , лежащую на перпендикуляре, восстановленном в центре круга, на расстоянии от плоскости круга? При каком значении эта сила будет наибольшей ( задано)?