Семинар 7

Криволинейные интегралы первого рода. Вычисление интегралов. Геометрические и физические приложения криволинейных интегралов первого рода.

Вводная информация

1. Определение криволинейного интеграла первого рода.

Пусть в каждой точке гладкой кривой , лежащей в плоскости , задана непрерывная функция двух переменных . Разобьем данную кривую на частей точками . Пусть - длина дуги . Возьмем на каждой дуге произвольную точку и составим сумму . Составленная сумма называется -ой интегральной суммой первого рода для функции , заданной на кривой . Обозначим через наибольшую из длин дуг . Если при существует предел интегральных сумм (не зависящий от способа разбиения кривой на части и выбора точек ), то этот предел называется криволинейным интегралом первого рода от функции по кривой и обозначается

или .

Если функция непрерывна, то криволинейный интеграл первого рода существует. Криволинейный интеграл первого рода обладает свойствами определенного интеграла (линейность, аддитивность и теорема о среднем), а также свойством (криволинейный интеграл первого рода не зависит от направления интегрирования).

2. Вычисление криволинейных интегралов первого рода.

Вычисление криволинейного интеграла первого рода сводится к вычислению определенного интеграла.

1. Пусть кривая задана непрерывно дифференцируемой функцией 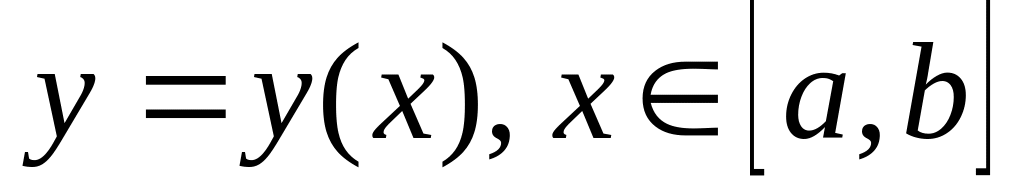, тогда

,

при этом выражение называется дифференциалом длины дуги.

2. Пусть кривая задана параметрически 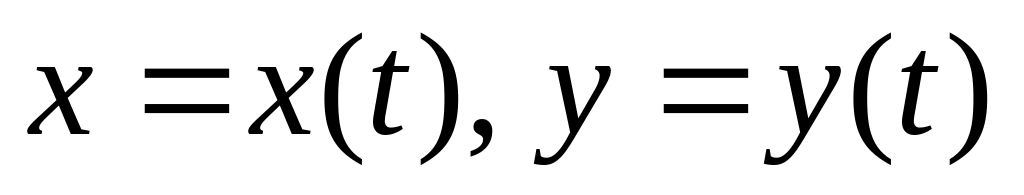, где - непрерывно дифференцируемые функции на отрезке 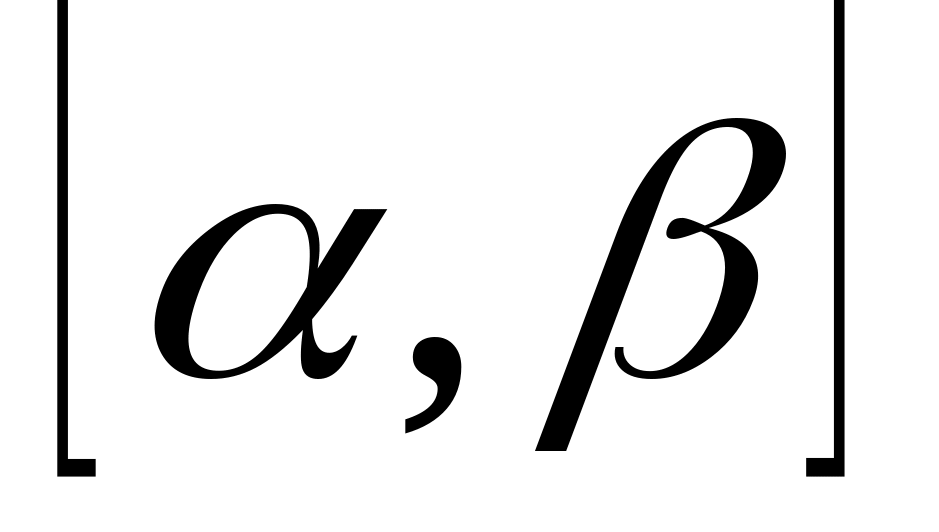, тогда

.

Аналогичная формула справедлива и для пространственной кривой , заданной параметрически

,

где - непрерывная функция вдоль кривой .

3. Пусть плоская кривая задана полярным уравнением 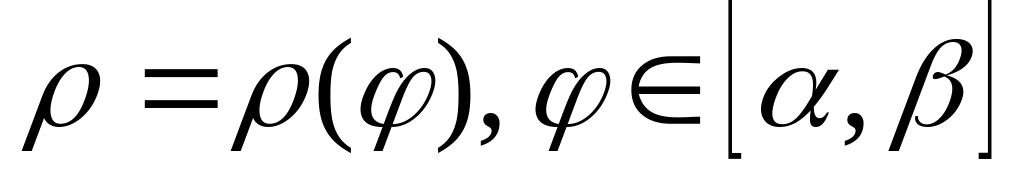, тогда

.

3. Приложения криволинейного интеграла первого рода.

1. Вычисление длины.

Используя криволинейный интеграл, можно вычислить длину кривой с помощью формулы

.

2. Вычисление площади цилиндрической поверхности.

Пусть в плоскости задана гладкая кривая , на которой определена непрерывная функция двух переменных . Тогда с помощью криволинейного интеграла можно вычислить площадь боковой поверхности цилиндроида с нижним основанием, ограниченным кривой , и верхним основанием, определенным поверхностью .

2. Вычисление массы материальной кривой.

Пусть - материальная кривая с линейной плотностью , тогда масса этой кривой вычисляется по формуле

.

2. Вычисление координат центра тяжести материальной кривой.

Статические моменты материальной кривой относительно координатных осей и соответственно равны

,

где - линейная плотность массы кривой , а координаты центра тяжести кривой определяются по формулам .

2. Вычисление моментов инерции кривой.

Криволинейные интегралы первого рода

определяют моменты инерции кривой с линейной плотностью относительно осей , и начала координат соответственно.

ЗАДАЧИ