Случайные величины и их числовые характеристики

Величина, принимающая свои значения в зависимости от исходов некоторого испытания, причем для каждого элементарного исхода имеющая одно единственное значение, называется случайной.

Числовые характеристики дискретной случайной величины

Математическое ожидание

Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных ее значений на соответствующие им вероятности:

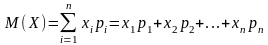
Свойства математического ожидания

1. Математическое ожидание постоянной величины равно самой постоянной:

, где .

2. Математическое ожидание алгебраической суммы нескольких случайных величин равно алгебраической сумме математических ожиданий этих величин:

.

Следствие. Если , то

3. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению математических ожиданий этих величин:

.

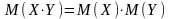Следствие. Постоянный множитель можно выносить за знак математического ожидания:

, где .

4. Математическое ожидание числа появлений события в 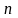независимых испытаниях (математическое ожидание биноминального распределения) равно произведению числа испытаний на вероятность появления события в каждом испытании: .

Дисперсия

Дисперсией дискретной случайной величины называется математическое ожидание квадрата отклонения этой величины от ее математического ожидания: .

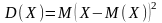Для вычисления дисперсии также можно использовать следующую формулу:

,

т.е. дисперсия случайной величины равна разности между математическим ожиданием квадрата этой величины и квадратом её математического ожидания.

Свойства дисперсии

1. Дисперсия постоянной величины равна нулю: , .

2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: , .

3. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин: .

4. Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин: .

5. Если , то .

Замечание 2. Для вычисления дисперсии биноминального распределения можно воспользоваться следующей формулой: , где – число испытаний; – вероятность осуществления события в одном испытании; – вероятность осуществления события 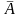(противоположного событию ) в одном испытании.

Среднее квадратическое отклонение

Средним квадратическим отклонением случайной величины называется квадратный корень из дисперсии: .

Замечание 3. На основании данного определения для обозначения диспер­сии часто используется символ .

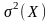Пример 1. Задан закон распределения дискретной случайной величины :

X	10	30	50	70	90
P	0,1	0,2	0,1	0,2	0,4

Найти:

1) математическое ожидание , дисперсию и среднее квадратическое отклонение ;

2) составить функцию распределения случайной величины и построить ее график;

3) вычислить вероятности попадания случайной величины в интервал , пользуясь составленной функцией распределения ;

4) составить закон распределения случайной величины ;

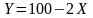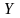5) вычислить математическое ожидание и дисперсию составленной случайной величины двумя способами: пользуясь свойствами математического ожидания и дисперсии, а также непосредственно по закону распределения случайной величины .