6 вопрос :

Условие плавания тел

Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести   и силы Архимеда  , которые действуют на это тело. Возможны следующие три случая:

•  — тело тонет;

•  — тело плавает в жидкости или газе;

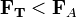•  — тело всплывает до тех пор, пока не начнет плавать.

Другая формулировка (где   — плотность тела,   — плотность среды, в которую оно погружено):

•  — тело тонет;

•  — тело плавает в жидкости или газе;

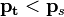•  — тело всплывает до тех пор, пока не начнет плавать.

Формулировка и пояснения

Закон Архимеда формулируется следующим образом^[1]: на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу вытесненной этим телом жидкости (или газа). Сила называется силой Архимеда:

где   — плотность жидкости (газа),   — ускорение свободного падения, а   — объём погружённого тела (или часть объёма тела, находящаяся ниже поверхности). Если тело плаваетна поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.

Тело плавает, если сила Архимеда уравновешивает силу тяжести тела.

Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.

Что касается тела, которое находится в газе, например в воздухе, то для нахождения подъёмной силы нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.

Закон Архимеда можно объяснить при помощи разности гидростатических давлений на примере прямоугольного тела.

где P_A, P_B — давления в точках A и B, ρ — плотность жидкости, h — разница уровней между точками A и B, S — площадь горизонтального поперечного сечения тела, V — объём погружённой части тела.

В теоретической физике также применяют закон Архимеда в интегральной форме:

,

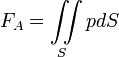где   — площадь поверхности,   — давление в произвольной точке, интегрирование производится по всей поверхности тела.

В отсутствие гравитационного поля, то есть в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции, поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами.

8 Вопрос :

Гидростатическое давление  — Благодаря полной малоподвижности своих частиц капельные и газообразные жидкости, находясь в покое, передают давление одинаково во все стороны; давление это действует на всякую часть плоскости, ограничивающей жидкость, с силой Р, пропорциональной величине w этой поверхности, и направленной по нормали к ней. Отношение Pw, то есть давление р на поверхность равную единице, называется гидростатическим давлением. Это основное свойство жидкостей было открыто и проверено на опытеПаскалем, в 1653 г., хотя несколько ранее оно было уже известно Стивену. Простое уравнение P = pw может действительно служить для точного вычисления давления на данную поверхность сосуда, газов и капельных жидкостей, находящихся при таких условиях, что часть давления, зависящая от собственного веса жидкостей, ничтожно мала по сравнению с давлением, передаваемым им извне. Сюда относятся почти все случаи давлений газов и расчеты давлений воды в гидравлических прессах и аккумуляторах. Условно-принятые меры Г. давления всегда выражают отношения силы к поверхности, поэтому в системе абсолютных единиц (см. Единицы мер) они выражают число «дин» на кв. см, именованное числоизмерения:

т ¹l⁻¹ - t⁻².

В практике Гидростатическое измеряют давление в кг на 1 кв. см. Большие давления выражают часто в атмосферах, принимая за 1 атмосферу давление в 76 см столба ртути, при температуре 0° под широтой, где ускорение силы тяжести = 0,0635 кг на 1 кв. см = 6,21·10⁶ дин на 1 кв. см. 1 атмосфера = 1,0333 кг на 1 кв. см = 1,0136·10⁶ дин на 1 кв. см для широты Парижа или 1,0132·10⁶ для широты в 45°. Вычисление немного усложняется, когда надо узнать давление, производимое на не горизонтальную часть стенки сосуда вследствие тяжести налитой на него жидкости. Здесь причиной давления становится вес столбов жидкости, имеющих основанием каждую бесконечно малую частицу рассматриваемой поверхности, а высотой вертикальное расстояние каждой такой частицы от свободной поверхности жидкости. Расстояния эти будут постоянны только для горизонтальных частей стенок и для бесконечно узких горизонтальных полосок, взятых на боковых стенках; к ним одним можно прилагать непосредственно формулу Г. давления. Для боковых же стенок надо суммировать, по правилам интегрального исчисления, давления на все горизонтальные элементы их поверхности; в результате получается общее правило: давление тяжелой жидкости на всякую плоскую стенку равняется весу столба этой жидкости, имеющему основанием площадь этой стенки, а высотой вертикальное расстояние её центра тяжести от свободной поверхности жидкости. Поэтому давление на дно сосуда будет зависеть только от величины поверхности этого дна, от высоты уровня жидкости в него налитой и от её плотности, от формы же сосуда оно зависеть не будет. Это положение известно под именем «гидростатического парадокса» и было разъяснено ещё Паскалем. Действительно, оно кажется на первый взгляд неверным, потому что в сосудах с равными днами, наполненных до равной высоты одной и той же жидкостью, вес её будет очень различный, если формы различны. Но вычисление и опыт (сделанный в первый раз Паскалем) показывают, что в сосуде, расширяющемся кверху, вес излишка жидкости поддерживается боковыми стенками и передается весам через их посредство, не действуя на дно, а в сосуде, суживающемся кверху, Г. давление на боковые стенки действует снизу вверх и облегчает весы ровно на столько, сколько весило бы недостающее количество жидкости. На основании сказанного выше можно Г. давление измерять также высотой столба ртути или воды, способного производить то же давление на единицу поверхности: так давление в 1 фн. на кв. дм. равно давлению столба воды в 25 дм высотой, так как фн. есть вес 25 куб. дм. воды.

Гидростатический парадокс — явление, при котором вес налитой в сосуд жидкости может отличаться от силы давления на дно.

[править]Причины

Причина гидростатического парадокса состоит в том, что жидкость давит не только на дно, но и на стенки сосуда. Вес жидкости в сосуде будет равен сумме высотных составляющих напора по всей внутренней площади сосуда. Если, к примеру, сосуд имеет участки внутренней поверхности, давление на которые направлено вверх, эти участки внесут вклад в вес со знаком минус. Статическое давление жидкости на дно окажется больше, чем вес жидкости, отнесённый к площади дна.

[править]Опыт Паскаля

Схема опыта Паскаля

В 1648 г. парадокс продемонстрировал Блез Паскаль. Он вставил в закрытую бочку, наполненную водой, узкую трубку и, поднявшись на балкон второго этажа, влил в эту трубку кружку воды. Из-за малой толщины трубки вода в ней поднялась до большой высоты, и давление в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула.