«Брестский государственный технический университет»

Кафедра информатики и прикладной математики

Курсовая работа «Исследование функции одной переменной на базе ЭТ Excel+VBA и СКМ MathCAD»










		Выполнил: студент гр. - Фамилия Имя Отчество Проверил: преподаватель: Фамилия И.О.







Брест 2013

Курсовая работа

Тема: Исследование функции y = f(x) на отрезке [a, b] в двух средах – Excel + VBA и MathCAD.

Варианты выдаются преподавателем !!!

Исследование функции включает этапы:

Анализ функции. Область определения функции.
Поиск точек разрыва функции, точек пересечения с осями координат.
Определение критических точек.
Установление чётности (нечётности) функции.
Исследование функции на монотонность (промежутки возрастания / убывания).
Определение интервалов выпуклости (вогнутости).
Построение графика функции.

Перечисленные задачи решаются в различных средах:

ЭТ Excel:
1. Построить таблицу значений функции одной переменной на интервале [a, b] с шагом h (отрезок разбить на 30 точек).
2. Отобразить заданную функцию графически.
3. Найти локальные максимум и минимум функции.
4. Найти корень функции методом табулирования, методом Ньютона и средством «Подбор параметра».
СКМ MathCAD:
1. Построить таблицу значений функции одной переменной на интервале [a, b] с шагом h (отрезок разбить на 30 точек), используя ранжированную переменную.
2. Построить график заданной функции.
3. Найти локальные экстремумы функции и определить их тип (при помощи первой производной; при помощи второй производной).
4. Найти в MathCAD первую f(x) и вторую f (x) производные функции в f(x) в аналитическом виде.
VBA:
1. Создать модули для табулирования функций f (x), f(x), f (x) .
2. Найти локальные экстремумы функции f (x).

Порядок выполнения работы в ЭТ Excel+VBA:

Построить таблицу значений и график заданной по варианту функции 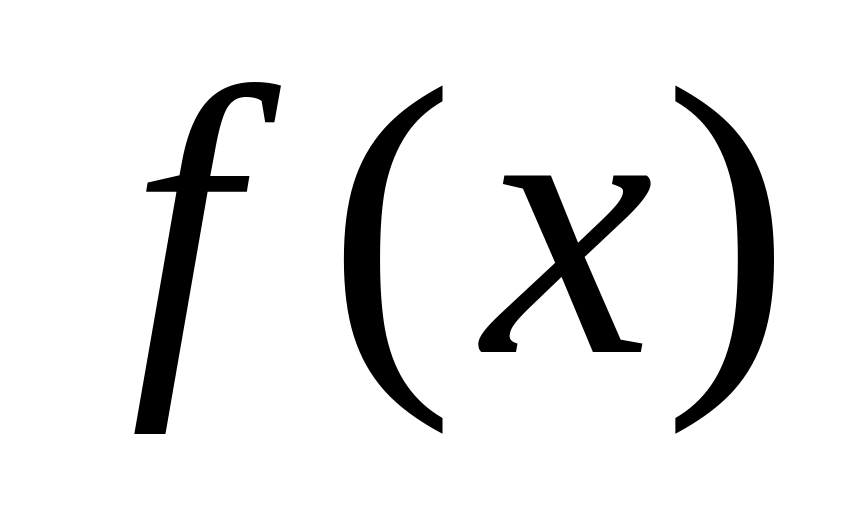на указанном отрезке 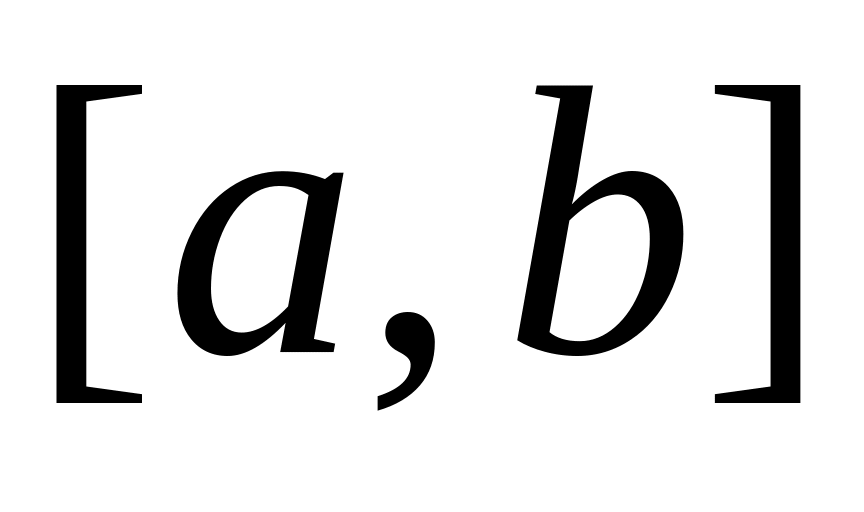при числе разбиений n = 30:

- задать отрезок, число разбиений и вычислить шаг табулирования.

- построить таблицу значений функции .

- используя ПИ «Форматирование», выполнить оформление таблицы.

- с помощью макрорекордера создать макрос для построения диаграммы и назначить его кнопке Вывод графика :

тип диаграммы – точечная, соединённая отрезками;
задать название диаграммы (График функции f(x)); легенду не выводить;
выполнить подписи по оси ОХ.
расположить диаграмму на имеющемся листе.

Найти корень 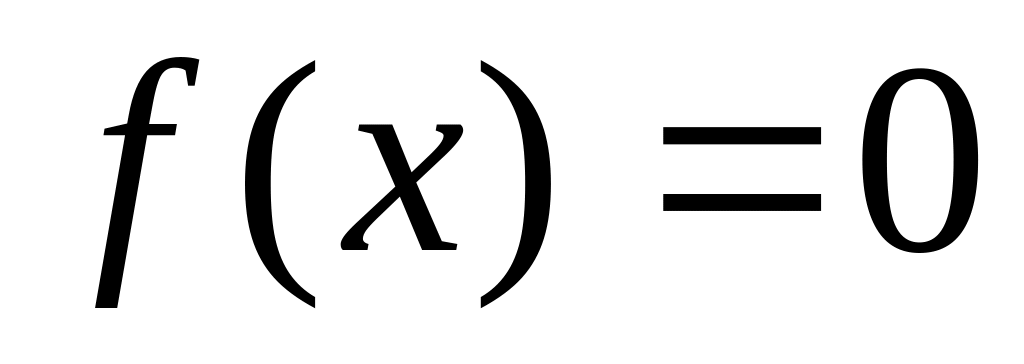с точностью ε=0,00001 методом табулирования, методом Ньютона и средством «Подбор параметра».
По таблице значений функции 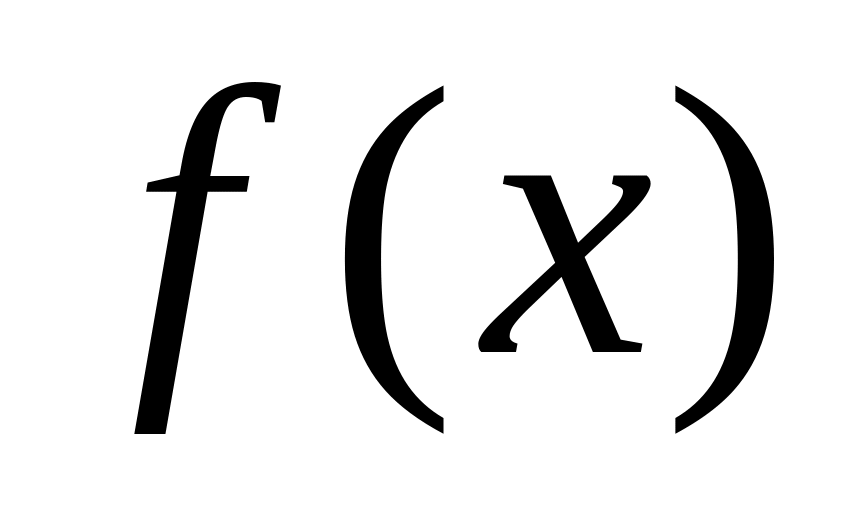найти точки локальных максимальных и минимальных значений функции и указать отрезки.
В ЭТ Excel+VBA создать пользовательские функции (Function) для f(x), f (x) f (x) (можно воспользоваться полученными аналитически производными функций в СКМ MathCAD).
С помощью созданных процедур построить таблицу значений функций f (x), f (x) f (x) на отрезке [a, b] с шагом h = (b – a) / n, где n=30 по образцу:

x

f(x)

f'(x)

f"(x)
Добавить на рабочий лист кнопку Построить графики для отображения на одной диаграмме графиков функций f (x), f (x), f (x) (тип диаграммы – «график» с маркерами, помечающими точки данных; легенду разместить внизу посередине).
Составить процедуру (Sub) для построения таблицы значений функций f(x), f (x) f (x) на отрезке [a, b] с шагом h = (b – a) / n, где n=30. Начало и конец отрезка, а также количество разбиений отрезка вводить с клавиатуры, используя функцию InputBox. Вывод результата организовать в окно Immediate в виде таблицы. В процедуре организовать вызов пользовательских функций, созданных выше.
Добавить в процедуру (Sub) поиск глобального максимума, глобального минимума функции. Результат вывести с помощью окна MsgBox.

Подготовить листы к печати:
1. установить колонтитулы – в верхнем колонтитуле по левому краю записать функцию f(x), по правому - ввести ФИО и номер группы; в нижнем колонтитуле по центру указать текущие дату и время;
2. установить при печати вывод заголовков строк и столбцов;
3. разместить задания на отдельных листах;

Порядок выполнения работы в СКМ MathCAD:

СКМ MathCAD найти локальные экстремумы функции двумя способами:

Блок Given…Maximize (Minimize);
С помощью производной.

Пусть в т. х=х₀ производная f’(x₀)=0. Если существует окрестность т. х₀ такая, что в этой окрестности f’(x)>0 при x<x₀ и f’(x)<0 при x>x₀, то функция имеет в т. х₀ максимум. Если же f’(x)<0 при x<x₀ и f’(x)>0 при x>x₀, то функция имеет в т. х₀ минимум.

Определить функцию, найти производную, построить графики соответствующих функций.
Найти нули производной, решив уравнение f’(x)=0 (использовать символьные вычисления: выделить переменную х в полученной функции производной и выбрать команду «Вычислить» (Solve) пункта «Переменные» (Variable) в меню «Символы» (Symbolic)).
Определить тип экстремумов (максимум/минимум), используя вычисление производной второго порядка. Вычислить для проверки значения производной в найденных точках и их окрестностях.

Решить те же задачи в MathCAD на базе встроенной функции root(), которая позволяет отыскивать корни при данном начальном приближении.

Сравнить результаты, полученные в Excel +VBA и MathCad !!!

Варианты функций:

a= -5 ; b=5 ; n=30

№ п/п	Функция f(x)	№ п/п	Функция f(x)
1		26
2		27
3		28
4		29
5		30
6		31
7		32
8		33
9		34
10		35
11		36
12		37
13		38
14		39
15		40
16		41
17		42
18		43
19		44
20		45
21		46
22		47
23		48
24		49
25		50