Лекція 6 Складність структурованих моделей

Основна мета розбивки повної системи на елементи, блоки та підсистеми - це побудова обмеженого набору співвідношень між характеристиками системи. У загальному випадку для повної складної системи ця задача виявляється непосильною. Тому звичайно доводиться розчленовувати систему на велику кількість елементів, математичний опис яких може бути виконано.

Для визначеності процесу декомпозиції введемо чисельну міру складності моделі. В основу цієї міри покладемо трудомісткість синтезу моделі, тобто витрати, необхідні для створення моделі. Назвемо цю міру складністю. Складність на стадії аналізу (стадії «чорного ящика») повинна враховувати лише число входів і виходів моделі (для простоти не будемо розрізняти керовані й некеровані входи). Нехай складність має вигляд . Наприклад, , де , тому що число входів сильніше впливає на складність, чим число виходів. Величину варто визначати залежно від того, у скільки разів збільшується трудомісткість синтезу моделі при збільшенні числа її входів на одиницю.

Функцією складності в деяких випадках можна вважати адитивною, тобто якщо модель об'єкта складається з декількох підсистем, те загальна складність дорівнює сумі складностей цих підсистем, тобто, де — складність підсистеми вихідного об'єкта.

З огляду на 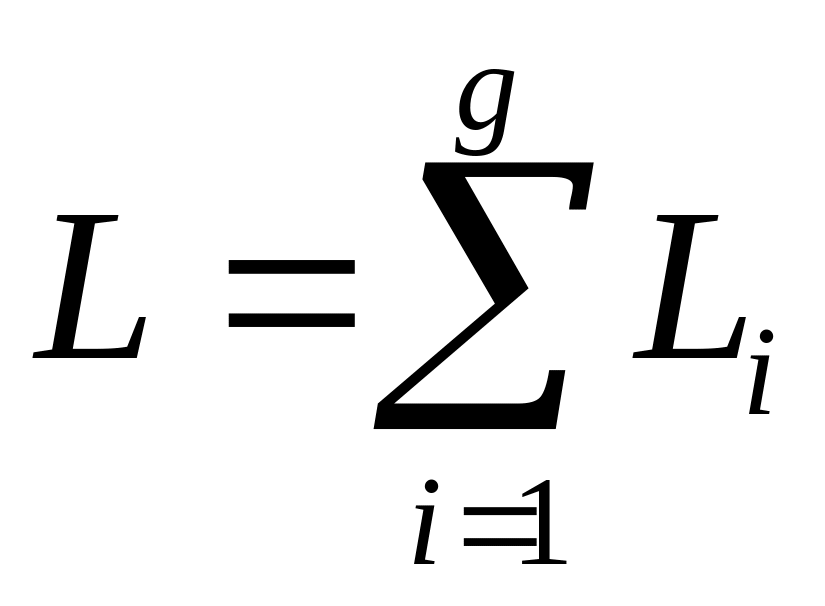сказане, процес декомпозиції моделі можна розглядати як процес мінімізації її складності, тобто як рішення наступної задачі мінімізації:

де — операція декомпозиції; — множина припустимих варіантів декомпозиції; — оптимальна декомпозиція, складність, що мінімізована , система, що декомпозована.

Таким чином, ціль декомпозиції моделі складається насамперед у тім, щоб спростити наступний синтез моделі об'єкта «розщепленням» її на більше прості елементи. Цей процес повинен вироблятися з урахуванням апріорної інформації про структурні особливості об'єкта.

Властивості та стани систем

Розглянемо множину систем . Для будь-якої окремої системи інші для яких , є середовище .

можна розглядати як множину непересічних підсистем. Підсистему також можна розглядати, що складається із множини непересічних підсистем нижчого рівня.

Для підсистем самого нижнього рівня в ієрархії визначень, що задають розбивку множини на непересічні підмножини, описи відповідають їхнім експериментальним властивостям. Систему, для якої всі властивості визначені експериментально (тобто опис її даний не через опис множини підсистем, її складових), назвемо елементом . В ієрархії визначень елементи перебувають на самому нижньому рівні:

.

Опис властивостей підсистем і систем більше високих рівнів може бути дане через опис властивостей підсистем більше низького рівня.

Експериментуючи з деякою підсистемою як з елементом (тобто не розділяючи на підсистеми), можна одержати її опис і тим самим зменшити кількість підсистем у моделі.

Стан всієї сукупності підсистем , а виходить, і всієї системи , що перебуває на найвищому рівні в системі визначень, позначимо :

де — простір станів сукупності розглянутих систем ; — простір станів ; — простір станів середовища (ці простори мають загальні координати); — координата вектора простору станів — дійсне число, що позначає величину, отриману при фізичних вимірах або спостереженнях.

Любою підсистемі відповідає сукупність властивостей (сукупність закономірностей її функціонування):

,

де — закономірність функціонування в певних умовах.

Властивості проявляються в результаті взаємодії із середовищем; у різних умовах можуть проявлятися різні властивості — закономірності функціонування системи або елемента.

Закономірність являє собою сукупність описів множини приватних закономірностей , що проявляють системою в умовах, які відповідають окремим конкретним експериментам. Закономірність — це функціональне співвідношення, що може бути задане як у вигляді формули (деякої аналітичної залежності), так й у вигляді таблиці окремих пар чисел, що відповідають (значення аргументу й функції, задані на деякій підмножині або всьому просторі станів ).

Таким чином, , де — експериментальний фізичний факт, що виявляє елементарну властивість системи й проявляється в певних умовах.

Початку процесу функціонування відповідно до , тобто конкретної реалізації фізичної закономірності, однозначно відповідає початковий стан середовища — і початковий стан підсистем , де стан а стан .

В кожен момент часу система й середовище перебувають в одному певному стані , що у загальному випадку може бути відомо лише з деякою ймовірністю.