Лекція 10

Лінійність або нелінійність стосовно вхідних сигналів — це не та ж саме, що лінійність або нелінійність вихідних змінних (функцій) по параметрах. Оператор і модель, що задає їм, називаються лінійними, якщо для системи справедлив принцип суперпозиції. Він полягає в тому, що лінійної комбінації довільних вхідних сигналів ставиться у відповідність та я лінійна комбінація сигналів на виході із системи:

Математичну модель із використанням лінійного оператор можна записати у вигляді .

Нелінійні рівняння, у свою чергу, можна розділити на два підкласи: алгебраїчні (у які над змінними робите тільки дії додавання, вирахування, множення, ділення й піднесення в ступінь із раціональним показником) і трансцендентні, у які входять інші функції від змінних (показові, тригонометричні та ін.). У кожному разі складність моделі істотно залежить від числа рівнянь і від виду вхідних у них функцій. Звичайно найбільше просто вирішуються алгебраїчні рівняння 1-й ступеня (лінійні), найбільше складно - трансцендентні.

Лінійні й нелінійні моделі. Лінійність або нелінійність аналізованого процесу впливає на вид моделі, метод програмування й швидкодія програми при її на практиці кількість продуктів і рівнянь, по яких ведеться розрахунок, становить кілька сотень, тому рішення таких задач вручну одержати досить важко.

У моделях виробничих процесів, крім рівнянь, можуть бути й нерівності.

У математичних моделях часто використається ряд нелінійних математичних структур, у першу чергу, це статечні поліноми. Методи інтерполяції дають можливість істотно спростити способи розрахунку коефіцієнтів статечного полінома при наявності точних даних про вхідні й вихідні параметри. Наприклад, при виборі як математична структура полінома виду

для даних з рівновіддаленими значеннями незалежної змінної коефіцієнти розраховуються по спрощеному способі:

,

де — крок інтерполяції; — різниця -го порядку. У результаті поліном записується у вигляді

називається інтерполяційним поліномом Ньютона.

В інтерполяційному поліномі Ньютона використаються раз отримані при русі по одну сторону від значення, узятого якості початкового. При використанні центральних разностей, отриманих у результаті застосування як наступних значень функцій (що випливають після значення, обраного в як початкового), так і попередніх, коефіцієнти полінома розраховуються в такий спосіб:

Увівши позначення , одержимо інтерполяційний поліном Гауса для рівновіддалених крапок інтерполяції:

Для нерівновіддалених вузлів інтерполяції використається інтерполяційний поліном Лагранжа

Особливе місце серед відомих математичних структур займають ортогональні поліноми. Ортогональним називається поліном

якщо всяка функція системи норма й дві різні функції й зазначена система функцій ортогональні в заданому інтервалі , тобто має місце рівність

Подібний вибір функцій дає можливість при квадратичному наближенні зробити спрощений розрахунок коефіцієнтів .

Найбільше часто використають ті ортогональні поліноми, для яких легко знайти вираження в явному виді. Такими є, наприклад, наведені нижче поліноми Чебишева, використовувані для проміжку [-1; +1]. Полином Чебишева першого роду визначається вираженням

де значення визначаються по вираженню

Для цілих позитивних значень це вираження є звичайним статечним поліномом, тому що

При зміні та у проміжку використається поліном Эрміта

Для періодичних функцій використаються тригонометричні поліноми

Кожна з математичних структур має свою специфіку, що та визначає область її застосування при моделюванні. Інтерполяційні поліноми використаються для об'єктів з відомими залежностями або з точними даними про значення вхідних і вихідних параметрів.

Моделі розподілені й зосереджені в просторі. Технологічний процес може бути розподіленим або зосередженим у просторі й одночасно змінюватися в часі. Моделі, що описують розподілені процеси, називаються моделями з розподіленими параметрами. Звичайно вони мають вигляд диференціальних рівнянь у частинних похідних. Якщо основні змінні процесу не змінюються в просторі, а тільки в часі, то математичні моделі, що описують такі процеси, називають моделями із зосередженими параметрами й представляють їх у вигляді звичайних диференціальних рівнянь.

Якщо процес розвивається одночасно й у часі, і в просторі (по одній координаті то оператор може перетворювати вхідну векторну функцію у вихідну векторну функцію й залежати від обох аргументів: .

Моделі безперервні й дискретні в часі. Безперервної в часі модель є в тому випадку, що коли характеризує її змінна визначена для будь-якого значення часу конкретної в часі, — якщо змінна отриманий; до у певні моменти часу. Безперервний у часі процес визначається моделлю , де може приймати будь-яке значення.

Так, якщо сигнал деякого компонента системи обгинає тільки в моменти часу те такий дискретний сигнал у моделюванні записують у вигляді послідовності . Дискретність моделі може також виникнути в тому випадку, її складається з безперервних компонентів, але інформація переходи однієї компоненти до іншої за заданою схемою (такі переходи можливі тільки по закінченні відповідних операцій).

Безперервні моделі застосовуються при вивченні систем, з безперервними процесами, які описуються за допомогою систем диференціальних рівнянь, що задають швидкість зміни змінні системи в часі. Безперервні моделі можна описати за допомогою кінцево-різницевих рівнянь, які в межу ходять у відповідні диференціальні рівняння. Програмування безперервних моделей зводиться до дискретної обчислювальної задачі, яку можна символічно записати рівняння

де , — відповідно вектори стану з компонентами, обумовленими в усі попередні моменти в; — вектор зовні системних змінних; — вектор параметри системи; — функція, що визначає поводження системи.

Кінцево-різницеві рівняння (лінійного й нелінійного, стаціонарного й нестаціонарні, рівняння першого й більше високого порядків, одномірні й багатомірні) дозволяють описати самі образні динамічні системи як з дискретним часом, у межі, з безперервним, тобто це досить універсально моделювання.

Розглянемо лінійне одномірне кінцеворазностні рівняння 7-го порядку з постійними коефіцієнтами. Припустимо спостереження виробляються в дискретні, рівновіддалені моменти часу. Приймемо також, що реакція на виході такої динамічної стаціонарної системи з'являється з деякою тимчасовою затримкою (на інтервалів квантування) стосовно вхідного сигналу. З урахуванням зазначених припущень запишемо кінцево-різницеве рівняння у вигляді

де — параметри рівняння; — номер чергового інтервалу квантування.

Лінійне кінцево-різницеве рівняння високого порядку подібного типу завжди можна замінити системою кінцево-різницевих рівнянь першого порядку, виражених у формі Коші, тобто дозволених щодо перших разностей. Ця обставина привела до того, що як найбільше загальний вид подання математичного опису стали широко використатися кінцево-різницеві моделі у формі Коші. Стаціонарна лінійна система може бути описана моделлю в стандартній формі:

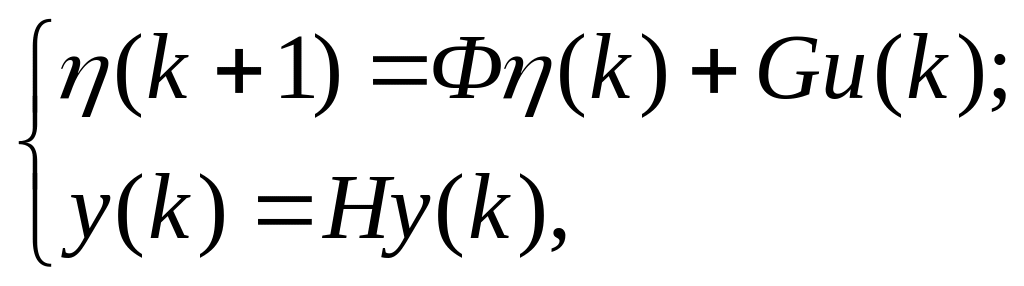
де , , — відповідно вектори відгуків, змінні стани й керуючих вхідних сигналів.

Матриці , і не залежать від моменту часу, тобто є постійними. Вони можуть включати невідомі параметри моделі, що підлягають оцінюванню. Наведену модель називають також канонічною формою моделі стаціонарної лінійної системи з дискретним часом. Якщо система нестаціонарна, то матриці , і будуть залежати від .

Нелінійна імпульсна система в досить загальному випадку може бути описана моделлю

де — векторні функції.

Дискретизація можлива не тільки по аргументі — часу, але й за рівнем (величині) сигналів. У цьому випадку сигнали мають кінцеве число значень у деякій заданій області існування. Подібні сигнали називають дискретними по величині або квантованими. І якщо безперервному скалярному сигналу відповідає плавна крива, те квантованому скалярному сигналу відповідає кусочно-постійна лінія (рис).

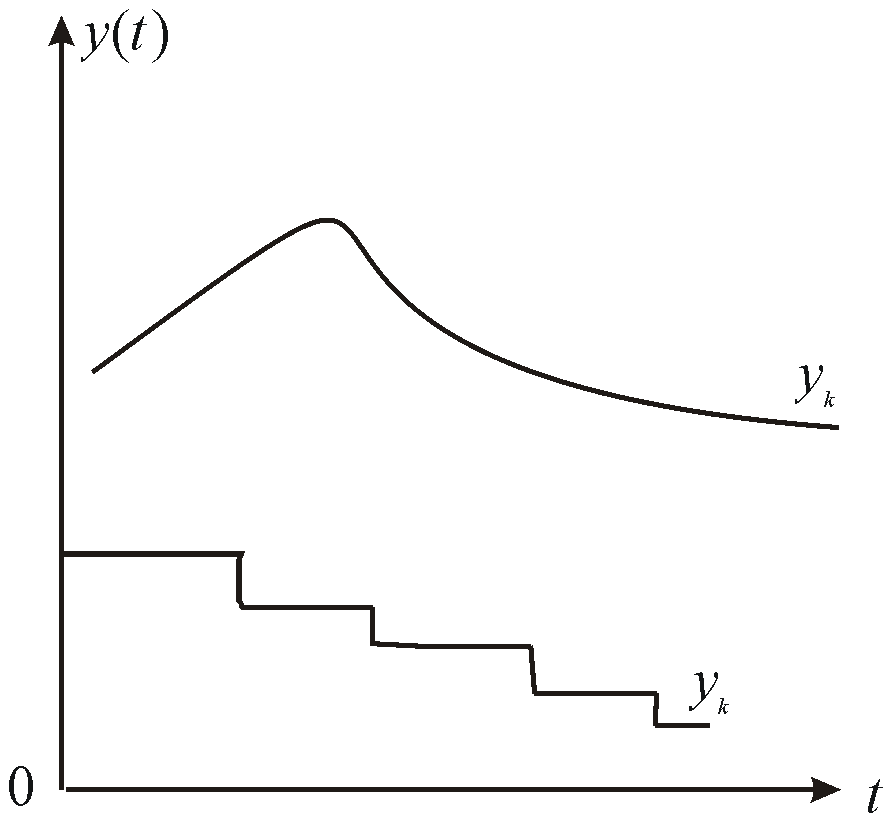
Рис. Безперервний і дискретний по величині сигнали

Системи (моделі), у яких вхідні й вихідні сигнали є безперервними за часом і по величині, називають безперервними. Якщо ж вхідні й вихідні сигнали дискретні за часом, то системи називають системами з дискретним часом або імпульсними. Системи, у яких вхідні й вихідні сигнали дискретні або за часом, або по величині, називають дискретними.

Існують також і системи проміжного типу, у яких властивості сигналів як функцій від часу різні. Наприклад, частина сигналів може бути безперервної в часі, тоді як інші сигнали можуть бути дискретними. Така система називається дискретно-безперервної за часом.