55 Дисципліна: «Комп’ютерне моделювання виробничих процесів»
Конспект лекцій
з дисципліни «Комп’ютерне моделювання
виробничих процесів»
лектор Новікова К.Ю.
Лекція 1
Слово "Модель" походить від латинського modus (копія, образ, обрис). Модель - це матеріальний або об'єкт, що представляє подумки, що заміщає в процесі вивчення об'єкт-оригінал, і що зберігає значимі для даного дослідження типові його риси. Процес побудови моделі називається моделюванням. Інакше кажучи, моделювання - це процес вивчення будови й властивостей оригіналу за допомогою моделі.
Метою моделювання є одержання, обробка, подання та використання інформації про об'єкти, які взаємодіють між собою й зовнішнім середовищем; а модель тут виступає як засіб пізнання властивостей і закономірності поводження об'єкта.
Класифікація моделей
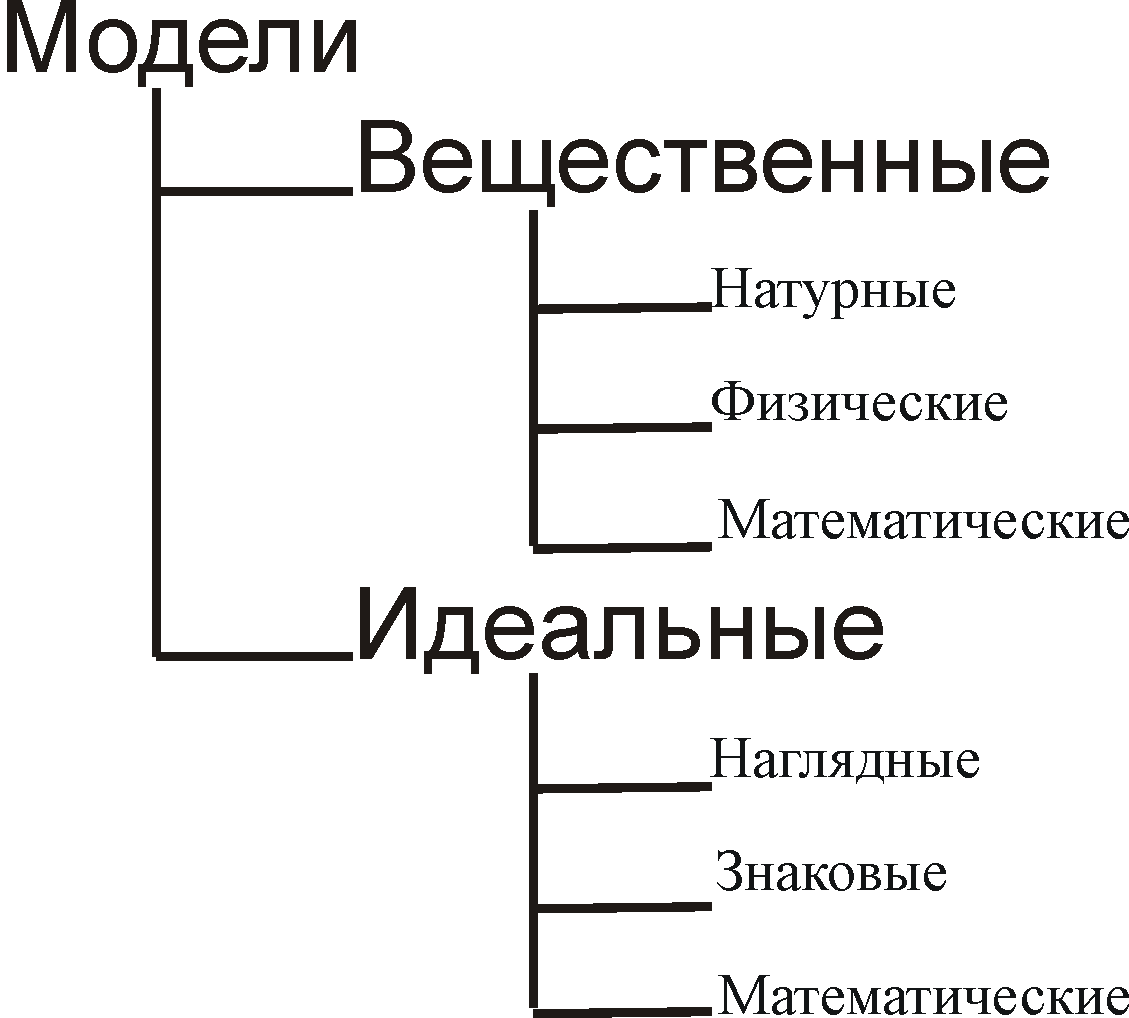
Всі моделі можна розділити на два класи:
речовинні,
ідеальні.
У свою чергу речовинні моделі можна розділити на:
натурні,
фізичні,
математичні.
Ідеальні моделі можна розділити на:
наочні,
знакові,
математичні.
Речовинні натурні моделі - це реальні об'єкти, процеси й системи, над якими виконуються експерименти наукові, технічні й виробничі.
Речовинні фізичні моделі - це макети, муляжі, що відтворюють фізичні властивості оригіналів (кінематичні, динамічні, гідравлічні, теплові, електричні, світлові моделі).
Речовинні математичні - це аналогові, структурні, геометричні, графічні, цифрові й кібернетичні моделі.
Ідеальні наочні моделі - це схеми, карти, креслення, графіки, графи, аналоги, структурні й геометричні моделі.
Ідеальні знакові моделі - це символи, алфавіт, мови програмування, упорядкована запис, топологічний запис, мережне подання.
Ідеальні математичні моделі - це аналітичні, функціональні, імітаційні, комбіновані моделі.
Схема процесу моделювання
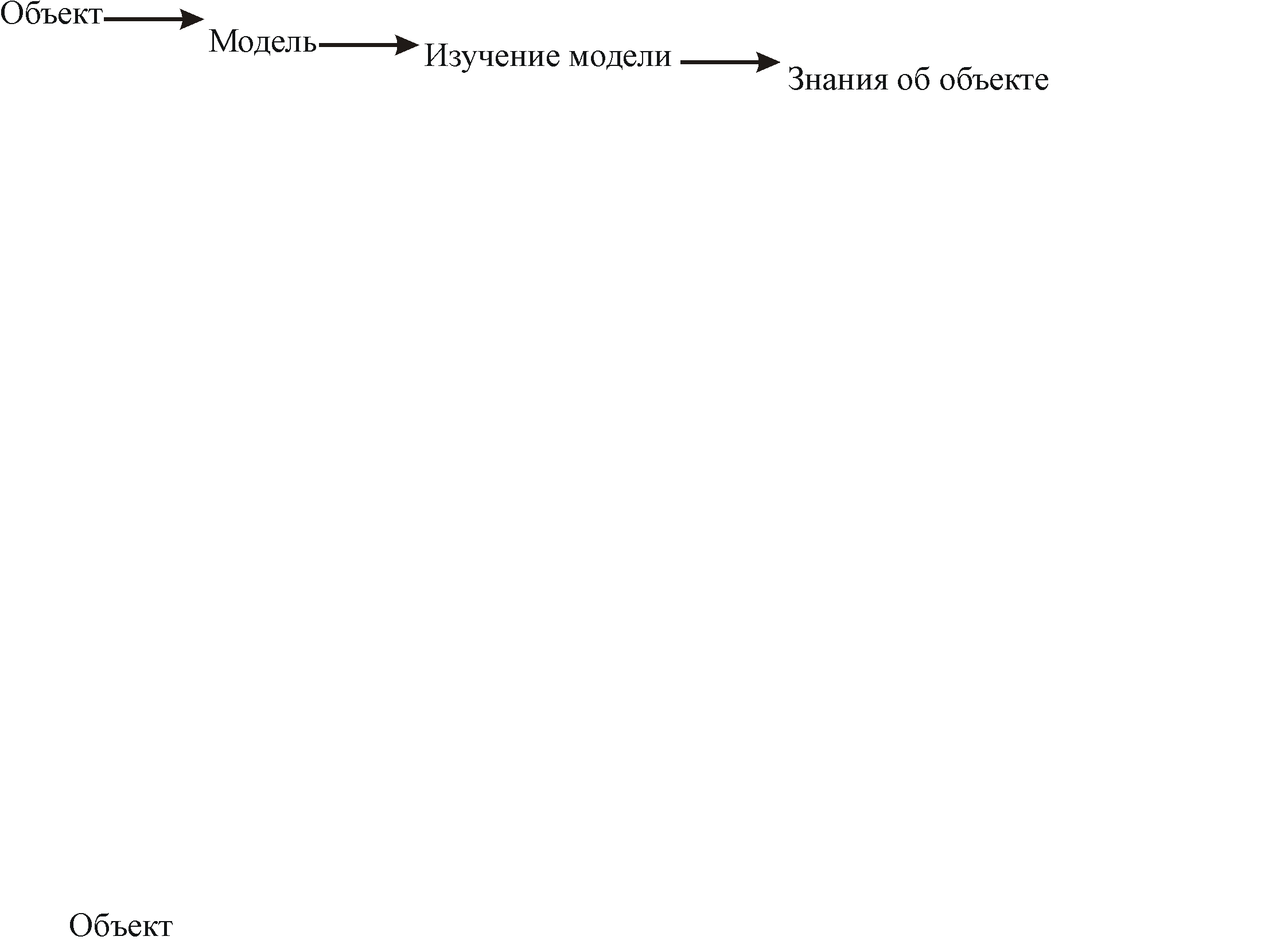
Для побудови моделей використають два принципи:
дедуктивний (від загального до частки)
індуктивний (від часткового до загального).
При першому підході розглядається окремий випадок загальновідомої фундаментальної моделі, що пристосовується до умов моделируемого об'єкта з урахуванням конкретних обставин. Другий спосіб припускає висування гіпотез, декомпозицію складного об'єкта, аналіз, а потім синтез.
Математичне моделювання
Математичне моделювання - це засіб вивчення реального об'єкта, процесу або системи шляхом їхньої заміни математичною моделлю, більше зручної для експериментального дослідження за допомогою ЕОМ.
Математична модель є наближеним поданням реальних об'єктів, процесів або систем, вираженим у математичних термінах і сохраняющим істотних рисах оригіналу. Математичні моделі в кількісній формі, за допомогою логіко-математичних конструкцій, описують основні властивості об'єкта, процесу або системи, його параметри, внутрішні й зовнішні зв'язки.
У загальному випадку математична модель реального об'єкта, процесу або системи представляється у вигляді системи функціоналів
Фi (X,Y,Z,t)=0,
де X - вектор вхідних змінних, X=[x1,x2,x3, ... , x]t,
Y - вектор вихідних змінних, Y=[y1,y2,y3, ... , y]t,
Z - вектор зовнішніх впливів, Z=[z1,z2,z3, ... , z]t,
t - координата часу.
Побудова математичної моделі полягає у визначенні зв'язків між тими або іншими процесами і явищами, створенні математичного апарата, що дозволяє виразити кількісно і якісно зв'язок між тими або іншими процесами і явищами, між фізичними величинами, що цікавлять фахівця, і факторами, що впливають на кінцевий результат.
По принципам побудови математичні моделі розділяють на:
аналітичні;
імітаційні.
В аналітичних моделях процеси функціонування реальних об'єктів, процесів або систем записуються у вигляді явних функціональних залежностей.
Аналітична модель розділяється на типи залежно від математичної проблеми:
рівняння (алгебраїчні, трансцендентні, диференціальні, інтегральні),
апроксимаційні задачі (інтерполяція, екстраполяція, чисельне інтегрування й диференціювання),
задачі оптимізації,
стохастичні проблеми.
Однак у міру ускладнення об'єкта моделювання побудова аналітичної моделі перетворюється у важкорозв'язну проблему. Тоді дослідник змушений використати імітаційне моделювання.
В імітаційному моделюванні функціонування об'єктів, процесів або систем описується набором алгоритмів. Алгоритми імітують реальні елементарні явища, що становлять процес або систему зі збереженням їхньої логічної структури й послідовності протікання в часі. Імітаційне моделювання дозволяє за вихідним даними одержати відомості про стани процесу або системи в певні моменти часу, однак прогнозування поводження об'єктів, процесів або систем тут важко. Імітаційні моделі - це проведені на ЕОМ обчислювальні експерименти з математичними моделями, що імітують поводження реальних об'єктів, процесів або систем.
Залежно від характеру досліджуваних реальних процесів і систем математичні моделі можуть бути:
детерміновані,
стохастичні.
У детермінованих моделях передбачається відсутність усяких випадкових впливів, елементи моделі (змінні, математичні зв'язки) досить точно встановлені, поводження системи можна точно визначити. При побудові детермінованих моделей найчастіше використаються алгебраїчні рівняння, інтегральні рівняння, матрична алгебра.
Стохастична модель ураховує випадковий характер процесів у досліджуваних об'єктах і системах, що описується методами теорії імовірності й математичної статистики.
По виду вхідної інформації моделі розділяються на:
безперервні,
дискретні.
Якщо інформація й параметри є безперервними, а математичні зв'язки стійкі, то модель - безперервна. І навпаки, якщо інформація й параметри - дискретні, а зв'язки нестійкі, те й математична модель - дискретна.
По поводженню моделей у часі вони розділяються на:
статичні,
динамічні.
Статичні моделі описують поводження об'єкта, процесу або системи в який-небудь момент часу. Динамічні моделі відбивають поводження об'єкта, процесу або системи в часі.
По ступені відповідності між математичною моделлю й реальним об'єктом, процесом або системою математичні моделі розділяють на:
ізоморфні (однакові за формою),
гомоморфні (різні за формою).
Модель називається ізоморфної, якщо між нею й реальним об'єктом, процесом або системою існує повна заелементна відповідність. Гомоморфною - якщо існує відповідність лише між найбільш значними складовими частинами об'єкта й моделі.
Подібність моделі з об'єктом, що вона відображає, називається ступенем ізоморфізму. Для того, щоб бути ізоморфної, модель повинна задовольняти двом умовам:
повинне існувати однозначна відповідність між елементами моделі й елементами об'єкта, що представляє;
повинні бути збережені точні співвідношення або взаємодії між елементами.
Ступінь ізоморфізму моделі відносна, і більшість моделей скоріше гомоморфні, чим ізоморфні.
Математичні моделі в кількісній формі, за допомогою логіко-математичних конструкцій, описують основні властивості об'єкта, процесу або системи, його параметри, внутрішні й зовнішні зв'язки.
Для побудови математичної моделі необхідно:
ретельно проаналізувати реальний об'єкт або процес;
виділити його найбільш істотні риси й властивості;
визначити змінні, тобто параметри, значення яких впливають на основні риси й властивості об'єкта;
описати залежність основних властивостей об'єкта, процесу або системи від значення змінних за допомогою логіко-математичних співвідношень (рівняння, рівності, нерівності, логіко-математичні конструкцій);
виділити внутрішні зв'язки об'єкта, процесу або системи за допомогою обмежень, рівнянь, рівностей, нерівностей, логіко-математичних конструкцій;
визначити зовнішні зв'язки й описати їх за допомогою обмежень, рівнянь, рівностей, нерівностей, логіко-математичних конструкцій.
Математичне моделювання, крім дослідження об'єкта, процесу або системи й складання їхнього математичного опису, також включає:
побудова алгоритму, що моделює поводження об'єкта, процесу або системи;
перевірка адекватності моделі й об'єкта, процесу або системи на основі обчислювального й натурного експерименту;
коректування моделі;
використання моделі.
Математичний опис досліджуваних процесів і систем залежить від:
природи реального процесу або системи й складається на основі законів фізики, хімії, механіки й т.д.
необхідній вірогідності й точності вивчення й дослідження реальних процесів і систем.