Содержание отчета

1. Перечень применявшихся аппаратов и приборов.

2. Схема цепи для исследования параллельного соединения индуктивной катушки и конденсатора (рис. 3).

3. Таблица 2 результатов измерений и вычислений.

4. Векторные диаграммы для трех случаев, данные по которым приведены в таблице 2.

5. Выводы.

6. Ответы на вопросы:

- в каких цепях и при каких условиях возникает резонанс токов?

- почему в момент резонанса токов сила тока в ветвях с индуктивностью и емкостью может быть значительно больше тока до разветвления?

-какие признаки указывают на наличие резонанса токов в цепи?

- как определить активную и индуктивную составляющие тока в ветви с катушкой?

- как влияет на cosj подключение емкости параллельно приемнику с индуктивностью?

- чему равен cosj при резонансе токов?

- чем вызывается необходимость повышения cosj в электроустановках переменного тока?

- в чем состоит пожарная опасность резонанса токов?

Л а б о р а т о р н а я р а б о т а № 3

Исследование цепей трехфазного тока при включении потребителей (активных сопротивлений) звездой.

Цель работы.

Исследование трехфазной системы при соединении потребителей (активных сопротивлений) звездой при равномерной и неравномерной нагрузке фаз, при аварийных условиях и определение роли нулевого провода.

Программа работы.

1. Исследование работы трехфазной системы при равномерной нагрузке фаз без нулевого провода и с нулевым проводом.

2. Исследование работы трехфазной системы при неравномерной нагрузке фаз без нулевого провода и с нулевым проводом.

3. Исследование работы трехфазной системы с нулевым проводом и без нулевого провода при обрыве одной из фаз для случаев равномерной и неравномерной нагрузки, а также при коротком замыкании одной из фаз и равномерной нагрузке фаз без нулевого провода.

Основные теоретические сведения по работе.

Для соединения потребителей звездой их концы соединяют между собой, а начала подключают к источнику трехфазного тока. Так как контакты активных сопротивлений не имеют обозначений «начало» и «конец», ибо совершенно безразлично к какому из них подключать начало фазы питающего напряжения, а к какому – конец, то для соединения активных сопротивлений в звезду достаточно соединить между собой по одному концу от каждого активного сопротивления, а другие – подключить к соответствующим фазам источника тока, если каждое из активных сопротивлений включается на фазное напряжение.

При таком способе включения потребителей и питающего их источника тока трехфазная система может быть четырехпроводной и трехпроводной.

При четырехпроводной системе потребители электроэнергии (активные сопротивления) находятся под фазным напряжением (рис.6).

Ток линейный при соединении звездой равен фазному, т.е. .

Сила тока в каждой из фаз зависит от величины фазного напряжения и сопротивления потребителей, включенных в эту фазу, т.е. .

Если сопротивления потребителей в каждой фазе равны между собой, то при равенстве фазных напряжений источника тока будут равны фазные токи, потребляемые активными сопротивлениями, и падения напряжения на активных сопротивлениях каждой из фаз, т.е. I_Ф1=I_Ф2=I_Ф3; U_Ф1=U_Ф2=U_Ф3.

Рис.6.Схема лабораторной установки

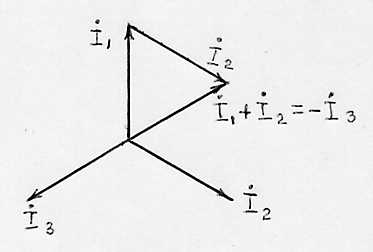
Рис.7. Векторная диаграмма токов при симметричной нагрузке.

Такая нагрузка называется равномерной (симметричной ). Ток в нулевом проводе можно определить по первому закону Кирхгофа, в соответствии с которым ,

где , , - линейные и фазные токи, потребляемые активными сопротивлениями.

При равномерной нагрузке фаз четвертый провод (нулевой) становится лишним, т.к. ток в этом случае равен нулю, что видно на рис. 7. В этом случае линейные U_Л и фазные U_Ф напряжения связаны соотношением: .

Приемники электрической энергии можно разделить на две группы. К первой относятся трехфазные электродвигатели, которые имеют симметричные обмотки и обеспечивают равномерную нагрузку фаз. Они включаются в трехфазную сеть звездой без нулевого провода.

Ко второй относятся электрические лампы, однофазные нагревательные приборы и другие приемники, которые не обеспечивают равномерную нагрузку фаз. Эти приемники электроэнергии всегда включаются звездой с нулевым проводом.

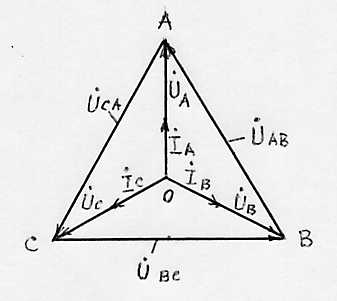
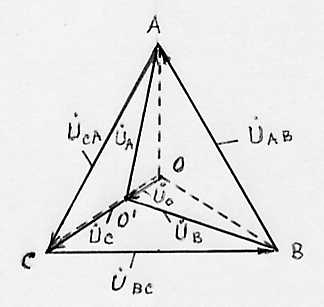
Рис. 8. Векторная диаграмма Рис. 9. Векторная диаграмма

напряжений и токов при напряжений при несиммет-

симметричной активной ричной нагрузке трехпровод-

нагрузке трехпроводной сети. ной сети.

Векторная диаграмма для симметричной активной нагрузки представлена на рис. 8.

Ее построение при известных линейных U_AB, U_BC, U_CA и фазных U_A, U_B, U_C напряжениях, а также известных токах I_A, I_B, I_C можно выполнить следующим образом. Строится треугольник АВС, стороны которого в выбранном масштабе равны линейным напряжениям U_AB, U_BC, U_CA. Из вершин треугольника АВС радиусом, равным в выбранном масштабе напряжений фазным напряжениям U_A, U_B, U_C, делаем засечки внутри треугольника АВС и находим точку О, которую соединяем с вершинами А, В, С, получая таким образом вектора фазных напряжений , , . При чисто активной нагрузке вектора токов , , будут направлены в фазе соответственно с векторами напряжений , , . Поэтому , выбрав масштаб для токов, откладываем отрезки, равные токам I_A, I_B, I_C из точки О в фазе с напряжениями , , , завершая построение векторной диаграммы для симметричной активной нагрузки трехпроводной и четырехпроводной трехфазных сетей, так как при симметричной нагрузке фаз ток в нулевом проводе четырехпроводной трехфазной сети отсутствует, и ее векторная диаграмма будет совпадать с векторной диаграммой трехпроводной трехфазной сети при активной симметричной нагрузке фаз.

Аналогично строятся векторные диаграммы и для несимметричной нагрузки трехпроводной (рис. 9) и четырехпроводной (рис. 10) трехфазных сетей.

При этом в первом случае, делая засечки из вершин треугольника АВС, стороны которого в масштабе напряжения равны линейным напряжениям , , , радиусами: из вершины А – радиусом, равным в масштабе

напряжения фазному напряжению U_A, из вершины В – радиусом, равным

в масштабе напряжения фазному напряжению U_B, из вершины С – радиусом, равным в масштабе напряжения фазному напряжению U_C, мы получим нулевую точку нагрузки О^¢, которая будет смещена относительно нулевой точки источника питания О на величину отрезка ОО^¢, который в масштабе напряжения представляет собой вектор , направленный из точки О в точку О^¢. Точку О можно получить, проведя из вершин треугольника АВС медианы (в равностороннем треугольнике медианы являются биссектрисами и высотами), которые пересекутся в точке О.

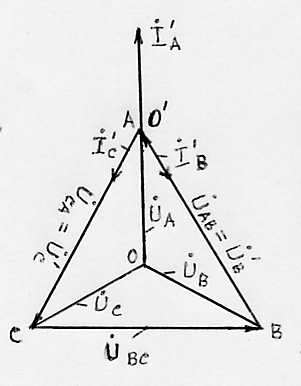
Рис. 10. Векторная диаграмма напряжений и токов при несимметричной активной нагрузке четырехпроводной сети.

Рис.11. Векторная диаграмма напряжений и токов при обрыве линейного провода и неравномерной нагрузке фаз четырехпроводной сети.

Отрезки О^¢А; О^¢В; О^¢С, направленные из точки О^¢ в вершины треугольника АВС, будут представлять собой вектора фазных напряжений , , .

Отрезки, равные в масштабе тока токам I_A, I_B, I_C. откладываем из точки О^¢ в фазе с напряжениями , , , получая таким образом вектора токов.

В трехпроводной трехфазной сети вектора токов в сумме дадут ноль, т.е. .

В четырехпроводной трехфазной сети фазные напряжения приемника по величине равны между собой и при неравномерной нагрузке фаз, если равны фазные напряжения источника тока . Векторная диаграмма для этого случая представлена на рис. 10. Для токов справедливо равенство , где - ток в нулевом проводе. При чисто активной нагрузке (активные сопротивления) токи , , откладываются из точки О в фазе соответственно с напряжениями , , . Векторная диаграмма для случая обрыва линейного провода, соединяющего фазы А источника питания и приемника при неравномерной нагрузке фаз и наличии нулевого провода, представлена на рис. 11. При этом U_A=0, а для токов будет справедливо равенство , а ток . В фазах С и В ток при обрыве линейного провода в рассматриваемом случае не изменится. Изменится только ток . Представленная на рис. 11 векторная диаграмма построена при измерении напряжений на зажимах приемника .

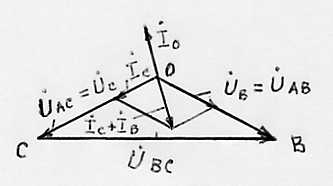
Векторная диаграмма для случая обрыва линейного провода, соединяющего фазы А источника питания и приемника при неравномерной нагрузке фаз без нулевого провода, представлена на рис. 12 (замеры напряжений производились на зажимах приемника).

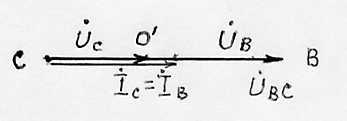
Рис.12. Векторная диаграмма напряжений и токов при обрыве линейного провода и неравномерной нагрузке фаз в трехпроводной сети.

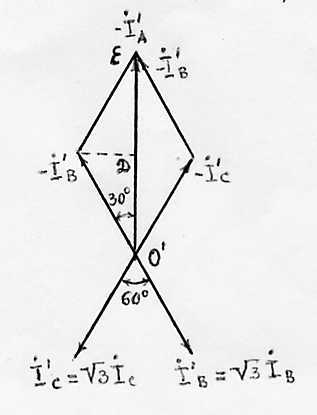
Рис. 13. Векторная диаграмма напряжений и токов при коротком замыкании фазы А и равномерной нагрузке трехпроводной сети.

Рис. 14. Векторная диаграмма токов при коротком замыкании фазы А и равномерной нагрузке трехпроводной сети.

В этом случае сопротивления нагрузки фаз С и В будут соединены последовательно и включены на линейное напряжение . По ним будет протекать один и тот же ток , а падения напряжения на сопротивлениях нагрузки фаз С и В ( и ) будут пропорциональны величине этих сопротивлений. Так как активные сопротивления создают чисто активную нагрузку, то ток будет в фазе с напряжением .

Векторная диаграмма для случая короткого замыкания фазы А при равномерной нагрузке фаз в трехфазной (без нулевого провода) сети представлена на рис. 13. При этом фазные напряжения и превратятся в линейные и возрастут в раз , возрастут в и токи в фазах В и С, а ток в фазе А увеличатся в 3 раза, что видно из рис. 14: ; .

Так как I_A=I_B=I_C, то .

Если в качестве нагрузки фаз включить электрические лампы накаливания, то при обрыве или отсутствии нулевого провода в случае неодинаковых сопротивлениях фаз нарушится равенство фазных напряжений,

следовательно, лампы накаливания, включенные в разные фазы, будут иметь неодинаковый накал: лампы, включенные в более нагруженные фазы (фазы, имеющие меньшие сопротивления) окажутся под меньшим напряжением и будут гореть с недокалом, а в менее нагруженные – под большим и могут перегореть. Это недопустимо, поэтому в нулевые провода не устанавливаются предохранители.

Порядок выполнения лабораторной работы.

1. Собрать схему, представленную на рис. 6.

2. При включенном нулевом проводе установить равномерную нагрузку фаз, измерить все напряжения (фазные и линейные) и токи. Убедиться, что U_Ф1= U_Ф2 = U_Ф3 и I₁ = I₂ = I₃; I_O = 0, а отключение нулевого провода не изменяет показаний приборов.

3. При включенном нулевом проводе установить неравномерную нагрузку фаз. Измерить все напряжения и токи.

Таблица 3

Характер нагрузки

Измерено

Вычислено

Нулевой провод

IA

IB

IC

I0

UAB

UBC

UCA

UA

UB

UC

PA

PB

PC

P

А

А

А

А

В

В

В

В

В

В

Вт

Вт

Вт

Вт

Равномерная

включен

отключ.

Неравно-мерная

включен

отключ.

Неравном. с обрывом одного линейного провода

включен

отключ.

Равномерн., одна из фаз закорочена

отклю-чен

4. При неравномерной нагрузке фаз отключить нулевой провод и записать показания приборов . Убедиться в перераспределении напряжений на фазах.

5. При неравномерной нагрузке фаз с нулевым проводом произвести обрыв одного из линейных проводов и записать показания приборов.

6. При неравномерной нагрузке фаз без нулевого провода произвести обрыв одного из линейных проводов и записать показания приборов.

7. Установить равномерную нагрузку фаз без нулевого провода, замкнуть накоротко одну из фаз и записать показания приборов.

8. Определить для всех указанных выше случаев фазные мощности и полную мощность цепи. Убедиться, что при равномерной нагрузке фаз Р = Р₁ + Р₂ + Р₃= , так как активные сопротивления создают чисто активную нагрузку, при которой cosj=1, а произведение равно полной мощности S.

Результаты измерений и вычислений записать в таблицу 3.

Содержание отчета.

1. Перечень применявшихся приборов и их данные.

2. Схема трехфазной четырехпроводной цепи при соединении приемников в звезду (рис.6).

3. Таблица результатов измерений и вычислений (табл.3).

4. Векторные диаграммы для четырех случаев нагрузки, данные по которым приведены в таблице 3.

5. Выводы.

6. Ответы на вопросы:

- доказать, что при соединении равномерной нагрузки звездой линейное напряжение больше фазного в раз;

- в чем заключается преимущество трехфазного тока перед однофазным током?

- для чего необходим нулевой провод в сетях освещения?

- почему при совместном питании электродвигателей и освещения применяются четырехпроводные сети?

- почему в нулевой провод нельзя устанавливать аппараты защиты?

- к чему приводит короткое замыкание одной из фаз при симметричной нагрузке, включенной звездой без нулевого провода?

- к чему приводит отключение одной фазы при неравномерной нагрузке, включенной звездой без нулевого провода?

- в чем состоит пожарная опасность аварийных режимов работы исследованной цепи?

Л а б о р а т о р н а я р а б о т а № 4

Исследование цепей трехфазного тока при включении потребителей (активных сопротивлений) треугольником.

Цель работы.

Исследование трехфазной системы при соединении потребителей электроэнергии (активных сопротивлений) треугольником при равномерной и неравномерной нагрузке фаз и при аварийных условиях.

Программа работы.

1. Исследование работы трехфазной системы при соединении потребителей электроэнергии треугольником при равномерной нагрузке фаз .

2. Исследование работы трехфазной системы при соединении потребителей электроэнергии треугольником при неравномерной нагрузке фаз.

3. Исследование работы трехфазной системы при соединении потребителей электроэнергии треугольником при равномерной нагрузке фаз и обрыве линейного провода.

Основные теоретические сведения по работе.

Для соединения трех нагрузочных сопротивлений в треугольник надо конец первого соединить с началом второго, конец второго – с началом третьего, конец третьего – с началом первого. При нагрузках, не имеющих электромагнитной взаимосвязи, т.е. исключающих однофазные двигатели и трансформаторы, начало и концы определяются произвольно. В качестве нагрузочных сопротивлений могут быть, например, три группы активных сопротивлений. Контакты выполненного таким образом соединения нагрузочных сопротивлений подключаются к линейным проводам трехфазной сети. Следовательно, каждое из трех нагрузочных сопротивлений включается на линейное напряжение трехфазной сети и представляет собой фазное сопротивление нагрузки, включенной треугольником. Поэтому при таком соединении выполняется равенство:

Включение трех групп активных сопротивлений в трехфазную сеть треугольником показано на рис.15.

Сила тока в каждой фазе равна

.

В зависимости от характера нагрузки фаз (активная или активно-индуктивная) фазные токи будут совпадать по фазе с напряжениями или отставать от них. Активно – емкостную нагрузку мы не рассматриваем, так как практически с ней не приходится иметь дело.

Рис.15. Схема лабораторной установки

Линейные токи на основании первого закона Кирхгофа равны:

.

При симметричной системе линейных напряжений на зажимах приемника и одинаковой (равномерной) нагрузке фаз приемника связь между величинами линейного и фазного токов выражается соотношением

I_Л = I_Ф.

Если в фазы приемника включены неодинаковые сопротивления (нагрузка приемника несимметричная) соотношение I_Л= I_Ф не выполняется и I_AB¹I_BC¹I_CA. Векторная диаграмма напряжений и токов для несимметричной нагрузки приемника представлена рис. 16.

Изменение сопротивления (нагрузки) одной из фаз приемника вызывает изменение двух линейных токов. Например, изменение фазного тока вызывает изменение линейных токов и .

Рис.16. Векторная диаграмма напряжений и токов при несимметричной нагрузке.

Рис.17. Векторная диаграмма напряжений и токов при симметричной нагрузке.

Фаза линейных токов также изменяется.

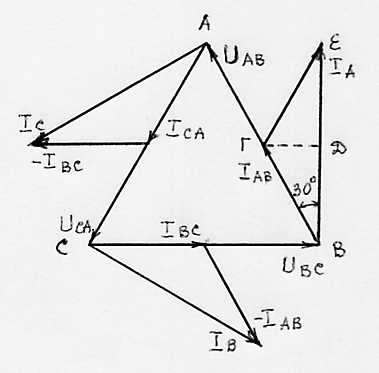
Векторная диаграмма напряжений и токов для симметричной (равномерной) нагрузки приемника представлена на рис. 17.

Из диаграммы видно, что линейные токи сдвинуты по фазе относительно фазных токов на 30^О. Отсюда легко доказать справедливость соотношения I_Л= I_Ф. Действительно, I_A=ВЕ=ВД+ДЕ; ВД=I_ABcos30^O=I_AB ; ДЕ=ВД=I_AB ; I_A=ВД+ДЕ=I_AB .

При исследовании трехфазного симметричного приемника, соединенного треугольником, особый интерес представляют следующие аварийные режимы:

-короткое замыкание фазы;

-внутренний обрыв одной из фаз приемника;

-обрыв одного из линейных проводов.

Короткое замыкание одной из фаз приемника, соединенного треугольником, по своему воздействию на цепь, аналогично короткому замыканию одной из фаз приемника, соединенного звездой с нулевым проводом. При таком замыкании происходит резкое увеличение фазного тока, величина которого становится опасной для всей цепи. Случайные короткие замыкания указанного вида должны немедленно отключаться защитой. Поэтому при проведении исследования приемника, соединенного треугольником, как и в случае соединения его звездой с нулевым проводом, короткое замыкание фазы не допускается.

При внутреннем обрыве одной из фаз приемника, соединенного треугольником, например, фазы АС, ток в этой фазе I_CА становится равным нулю. Режим работы фаз АВ и ВС остается без изменения, так как напряжение на этих фазах не изменяется.

Не изменится также линейный ток , а линейные токи I_A и I_C станут равными фазным токам.

При обрыве одного из линейных проводов при соединении треугольником, например, линейного провода В, фаза АС будет продолжать работать в прежнем режиме, так как она останется включенной на напряжение U_{AC .} Две другие фазы окажутся соединенными последовательно к этому же напряжению U_AC, которое распределится между ними (при одинаковых сопротивлениях фаз) поровну. При этом аварийном режиме трехфазная система превращается в однофазную, поэтому токи в линейных проводах А и С будут сдвинуты относительно друг друга на 180^О т.е. .

При симметричном приемнике (равных сопротивлениях фаз) фазные токи I_AB и I_BC уменьшатся вдвое, соответственно уменьшению напряжения на этих фазах.

При неизменном значении тока I_CA=I_Ф токи в уцелевших линейных проводах будут:

; , т.е. эти токи уменьшаются по сравнению с нормальным режимом работы приемника в раз .

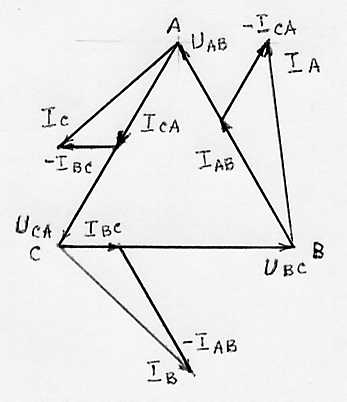
Векторная диаграмма для случая обрыва линейного провода представлена на рис. 18.

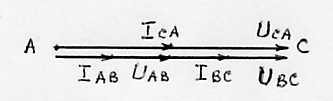
Рис. 18. Векторная диаграмма напряжений и токов при обрыве линейного провода

Порядок выполнения лабораторной работы.

1. Собрать схему трехфазной сети при соединении трех групп активных сопротивлений в треугольник (рис.15).

2. Установить равномерную нагрузку фаз и измерить линейные и фазные токи, а также напряжения; убедиться, что при такой нагрузке .

Таблица 4

Характер Нагрузки

Измерено

Вычислено

IAB

IBC

ICA

IA

IB

IC

UAB

UBC

UCA

P1

P2

P3

P

A

A

A

A

A

A

B

B

B

Вт

Вт

Вт

Вт

Равномерн. нагрузка трех фаз

Неравном. нагрузка трех фаз

Обрыв лин. провода при равном. нагрузке фаз

3. Установить неравномерную нагрузку фаз и измерить линейные и фазные токи, а также напряжения; убедиться, что при соединении потребителей треугольником изменение нагрузки одной фазы не влияет на нагрузку двух других фаз.

4. При равномерной нагрузке фаз отключить один линейный провод и измерить линейные и фазные токи, а также напряжения; установить, как влияет обрыв линейного провода на работу приемника.

5. Определить для всех, указанных выше случаев, фазные мощности приемника Р₁, Р₂, Р₃, соединенного треугольником, и его суммарную мощность Р:

Р=Р₁+Р₂+Р₃; убедиться, что при равномерной нагрузке фаз

Р=Р₁+Р₂+Р₃= cosj (для активной нагрузки, создаваемой активными сопротивлениями cosj=1).

Результаты измерений и вычислений занести в таблицу 4.

Содержание отчета.

1. Перечень применявшихся приборов и их данные.

2. Схема трехфазной цепи при соединении приемников в треугольник (рис.15).

3. Таблица результатов измерений и вычислений (табл.4).

4. Векторные диаграммы напряжений и токов для трех исследованных случаев нагрузки, данные по которым приводятся в таблице 4.

5. Выводы и объяснение влияния обрыва одного из линейных проводов на работу приемника при равномерной и неравномерной нагрузке фаз .

6. Ответы на следующие вопросы:

- доказать, что при соединении приемника в треугольник с одинаковой нагрузкой фаз справедливо равенство ;

- к чему приведет обрыв одного линейного провода при соединении симметричной нагрузки треугольником?

- к чему приведет короткое замыкание нагрузки одной фазы при соединении трехфазного приемника треугольником?

- изменятся ли фазные напряжения приемника, соединенного треугольником, при отключении одной фазы нагрузки?

- в чем состоит пожарная опасность аварийных режимов работы исследованной цепи?