Решение однородного линейного дифференциального уравнение 2-го порядка с постоянными коэффициентами

линейное однородное дифференциальное уравнение 2-го порядка.

характеристическое уравнение.

Корни характеристического уравнения	Вид решения
1. k1, k2 – действительные различные корни
2. k=k1=k2; k1, k2 – действительные равные корни
3. k1, 2= k1, k2-комплексные корни

Пример 22

;

Характеристическое уравнение ; k₁=1, k₂=2;

Общее решение

Пример 23

; ; ;

Общее решение

Пример 24

; ; ; ,

Общее решение ─ .

Решение неоднородного линейного уравнения 2-го порядка с постоянными коэффициентами

─ линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами p и g.

Общее решение неоднородного уравнения имеет вид

─ общее решение соответствующего однородного уравнения;

─ частное решение неоднородного дифференциального уравнения.

Для подбора частного решения по виду правой части f(x) и корней характеристического уравнения можно пользоваться следующей таблицей.

Рассмотрим только те случаи, в которых корни характеристического уравнения – действительные числа.

Правая часть уравнения f(x)	Корни характеристическо-го уравнения	Вид частного решения уравнения
1. ─ действительное число ─ многочлен степени n>0 относительно x.	а) ─ не является корнем характеристическо-го уравнения, т.е ,
	б) ─ является корнем характеристическо-го уравнения = ,
	в) ─ является двукратным корнем характеристичес-кого уравнения

Пример 25

однородное дифференциальное уравнение 2-го порядка.

Правая часть ─ многочлен 2-ой степени, .

Найдём общее решение соответствующего однородного уравнения.

характеристическое уравнение; ; ─ корни уравнения различные, общее решение соответствующего однородного уравнения ─

Найдём частное решение неоднородного дифференциального уравнения,

т. к. не является корнем характеристического уравнения, т. е. ,

, то вид частного решения ; ; . Найдём ; и подставим полученные выражения в исходное уравнение

; ;

Приравниваем коэффициенты при соответствующих степенях x в левой и правой частях уравнения

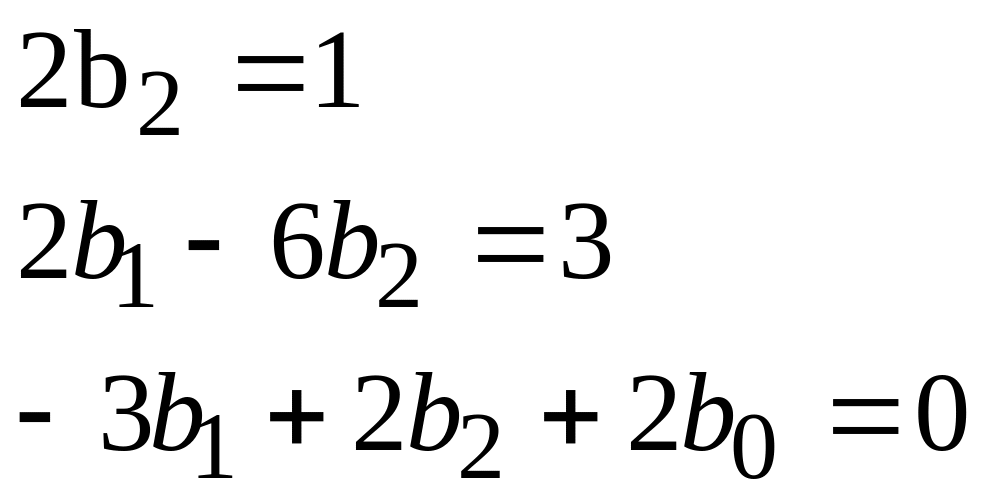, решая систему, получим .

Тогда частное решение

Общее решение неоднородного дифференциального уравнения имеет вид

.

Пример 26

; ; ; ,

; ; − многочлен нулевой степени, , ; корень характеристического уравнения, следовательно, частное решение будем искать в следующем виде: ;

; ;

; ; ; ; . Общее решение .

Пример 27

.

; ; ; ,

─ общее решение соответствующего однородного уравнения.

0, ─ двукратный корень характеристического уравнения

, n=0, , ;

; ;

; ; ; .

Общее решение ─ .