3.9 Электрическая схема корректирующего устройства

По передаточной функции составим электрическую схему корректи­рующего устройства. Для этого сначала перепишем ее в стандартном виде с учетом новых обозначений постоянных времени :

,

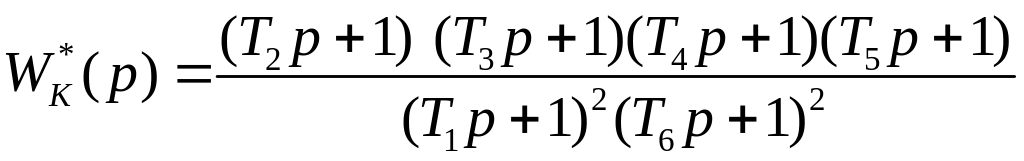где , , , , , .

Способ 1. Представим в виде произведения четырех передаточных функций типовых корректирующих цепей:

.

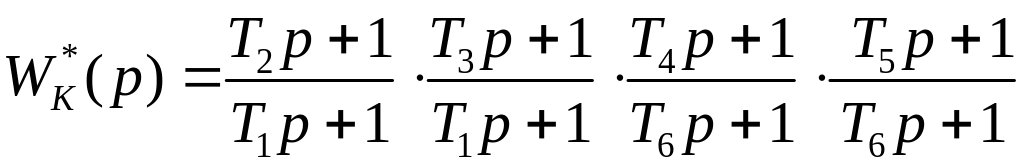Поскольку , то первым двум передаточным функциям будут соответствовать пассивные интегрирующие цепочки, разделенные повторителем напряжения для исключения взаимного влияния цепей, в результате которого изменяется общая передаточная функция. Учитывая, что , последним двум передаточным функциям будут соответствовать активные дифференцирующие цепи.

В соответствии с таблицей П.1 электрическая схема корректирующего устройства с передаточной функцией представлена на рис. 27.

Рис. 27

По известным значениям постоянных времени, задаваясь величиной емкости мкФ, найдем величины:

первый каскад

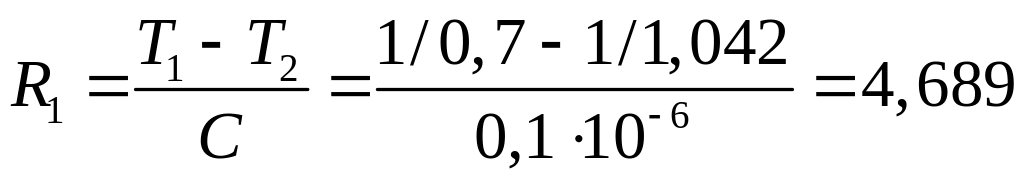Мом, Мом;

второй каскад

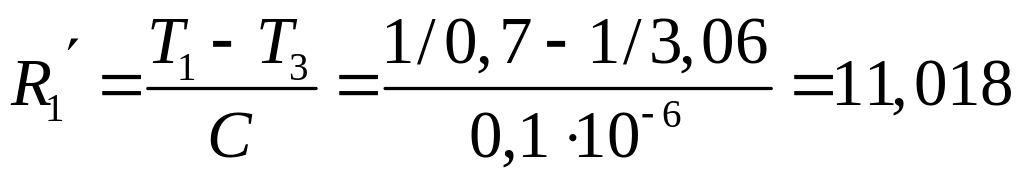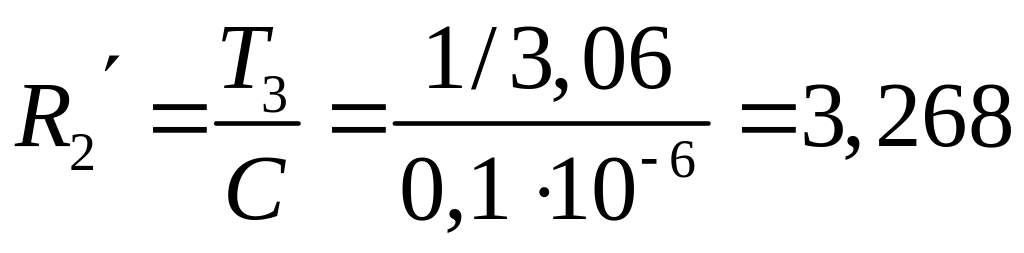Мом, Мом;

Здесь малым выходным сопротивлением операционного усилителя пренебрегаем по сравнению с сопротивлением .

третий каскад

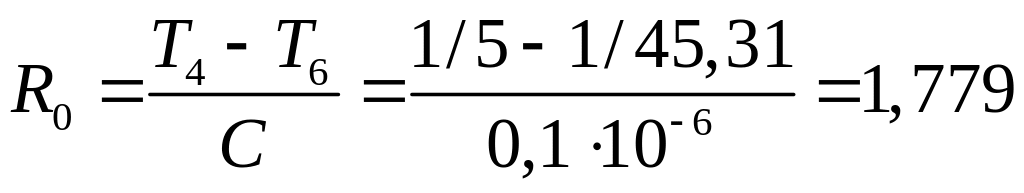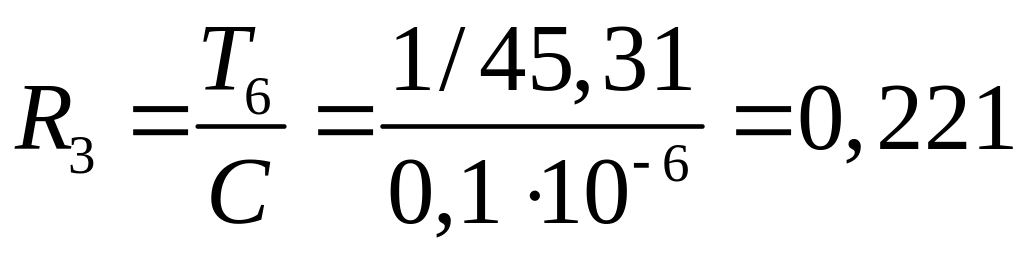Мом, Мом;

четвертый каскад

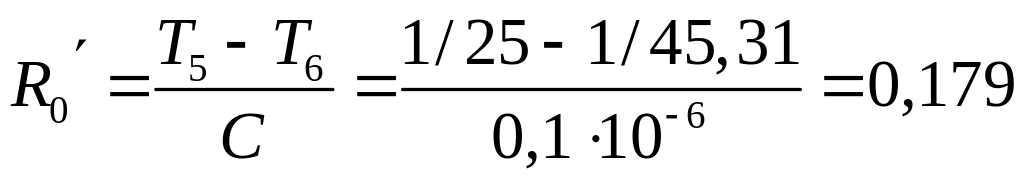Мом, Мом.

Способ 2. Учитывая, что , и , , представим в виде произведения

,

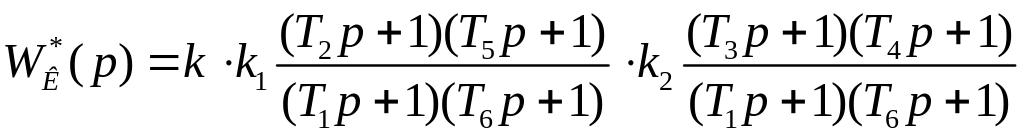где , , .

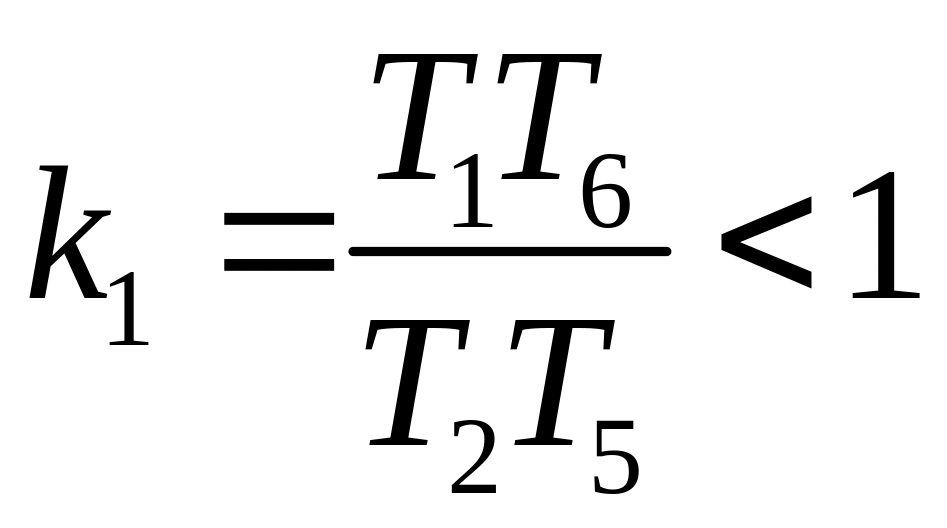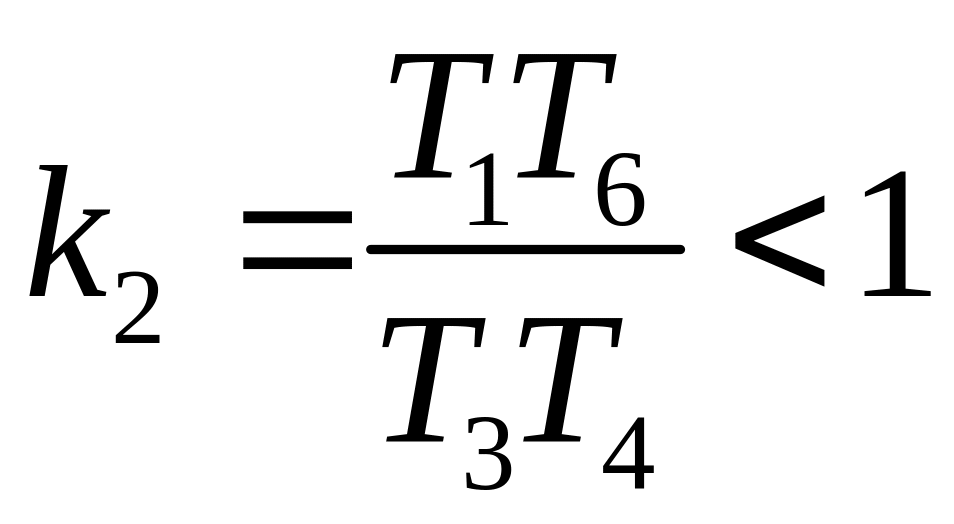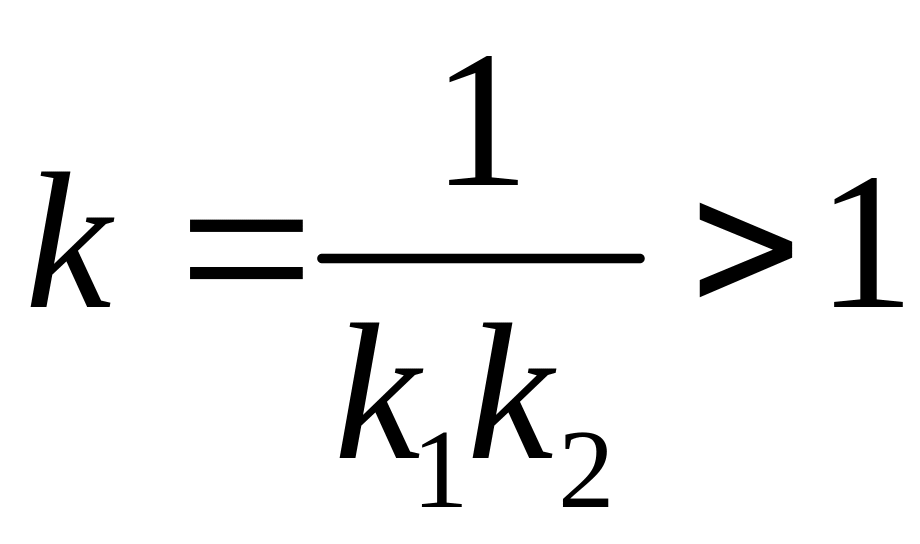Тем самым для реализации корректирующего устройства согласно таблице П.1 необходимо использовать две интегро-дифференцирующие цепи, разделенные усилителем с коэффициентом усиления (рис. 28).

Рис. 28

По известным значениям постоянных времени, задаваясь величиной электроемкостей мкФ, мкФ найдем величины:

первый каскад

0,96 Мом, ,

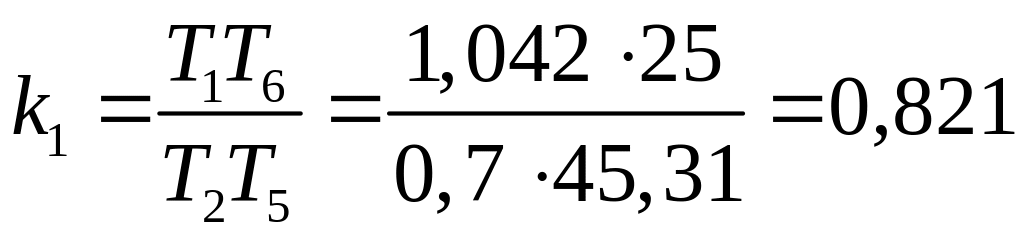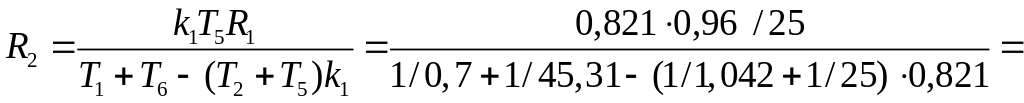0,069 Мом,

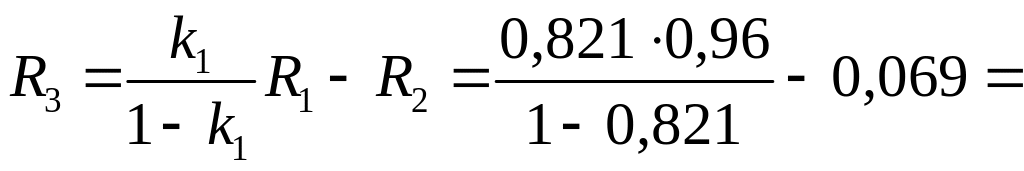4,33 Мом,

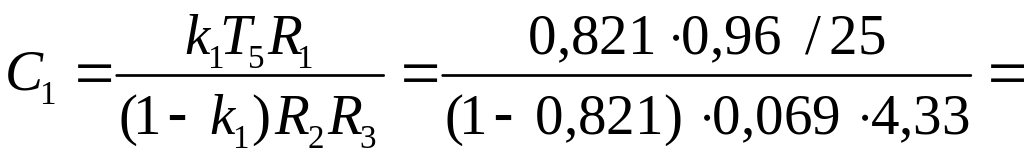0,589 мкФ;

второй каскад

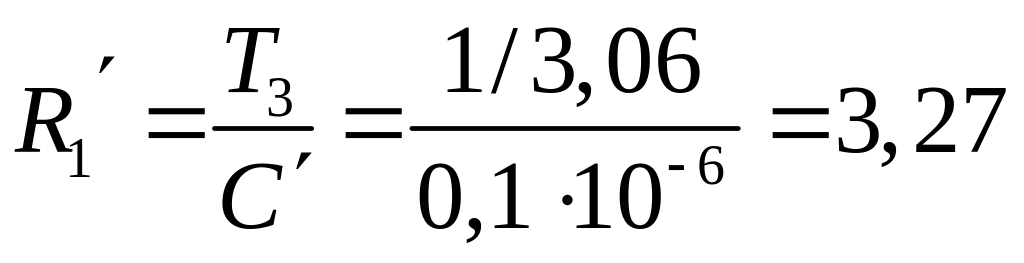Мом, 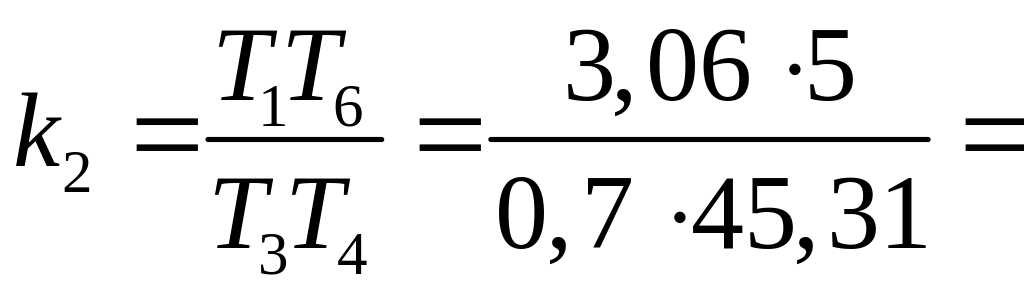0,482,

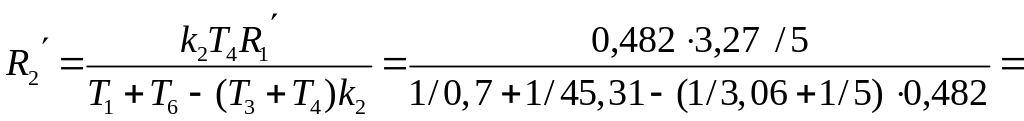0,26 Мом,

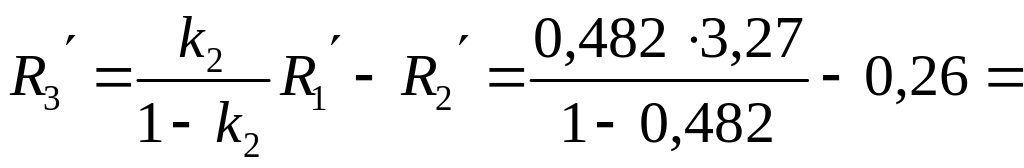2,78 Мом,

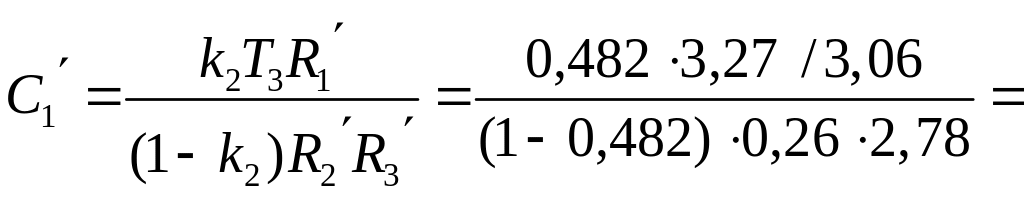1,37 мкФ;

неинвертирующий операционный усилитель

полагая Мом, найдем

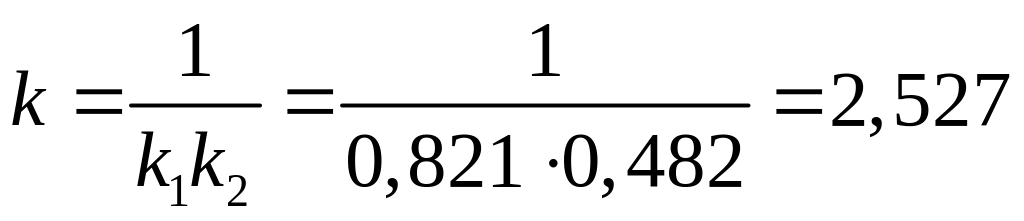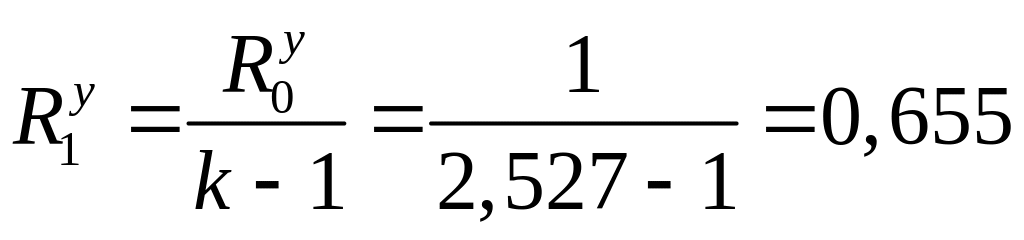, Мом.

Учитывая, что сопротивления , , , , , имеют значения порядка Мом, для операционного усилителя будет выполнено ограничение по току [30, с. 16-17].

Таким образом, второй способ реализации корректирующего устройства проще и экономичнее первого.

Окончательный выбор найденных элементов электрической схемы осуществляется с помощью номинальных паспортных элементов. Если при этом постоянные времени передаточной функции корректирующего устройства будут отличаться от расчетных больше чем на 3%, то необходимо построить переходную характеристику замкнутой системы с полученной передаточной функцией корректирующего устройства и проверить выполнение условий , . При нарушении данных условий необходимо доопределить параметры элементов корректирующего устройства.

Оценить влияние изменения постоянных времени передаточной функции корректирующего устройства на качество переходных процессов замкнутой системы также можно с помощью ЛАХ и ЛФХ нескорректированной и желаемой системы.

3.10 Синтез дискретного корректирующего устройства

На практике часто возникает задача замены непрерывных регуляторов дискретными регуляторами, как более надежными и эффективными средствами управления. При этом необходимо, чтобы дискретная система обладала теми же свойствами, что и непрерывная.

Структурная схема системы с дискретной коррекцией представлена на рис.29, где сигнал с идеального импульсного элемента поступает на вход передаточной функции дискретной коррекции, выходной сигнал которой поступает на формирователь прямоугольных импульсов (фиксатор нулевого порядка) длительностью . Тем самым на вход объекта управления с передаточной функцией поступает кусочно-постоянный сигнал: при ,

Рис. 29