VI. Понятие тензора.

Вернемся к билинейным функционалам . Множество таких билинейных функционалов образует векторное пространство с бинарной операцией и правилом умножения на число . Это пространство обозначается . Поскольку элементами этого пространства являются отображения, то и базисными векторами будут отображения. Эти базисные векторы можно построить из векторов сопряженного базиса пространства как всевозможные пары , здесь - символ тензорного умножения. Относительно такого базиса разложение билинейного отображения имеет вид

,

где - коэффициенты билинейного отображения . Закон преобразования этих коэффициентов (координат) мы уже приводили

.

Рассматривая билинейные функционалы вида , мы получим векторное пространство , которое еще обозначают . Базисом этого пространства будут тензорные произведения , относительно которого разложение билинейного функционала имеет вид

,

где - коэффициенты функционала, преобразующиеся по закону

.

Наконец, вводя билинейные функционалы , придем к векторному пространству , разложение векторов которого по базису дается выражением

,

где с законом преобразования

.

Мы рассмотрели линейные функционалы и билинейные функционалы. В общем случае можно ввести понятие полилинейного отображения , линейного по каждому аргументу. Все множество таких отображений также является векторным пространством, которое обозначается , где - число слагаемых во внешней прямой сумме, а - число слагаемых . Элементы векторного пространства называются тензорами типа , имеющими валентность . Говорят также, что введенные тензоры являются смешанными тензорами: раз ковариантными и раз контрвариантными. Разложение тензора по базису имеет вид

,

где . Ясно, что при переходе к другому базису тензор (элемент векторного пространства!) не изменяется, а преобразуются его координаты

.

Итак, каждому тензору можно поставить в соответствие -мерную матрицу . Обратно, каждой такой матрице соответствует свой тензор – элемент векторного пространства . Такое соответствие определяет изоморфное отображение между векторными пространствами и пространством -мерных матриц . Размерность пространства таких матриц равна . Следовательно, размерность векторного пространства также равна . Построенный изоморфизм позволяет несколько по-другому определить тензор.

Определение. Тензором типа валентности называется объект, который задается в некоторой системе координат набором чисел , преобразующихся по тензорному закону

,

при замене системы координат .

В соответствии с определением вектор является тензором типа , а ковектор - тензором типа . Оба имеют валентность, равную единице.

Можно определить различные операции над тензорами.

1. Сложение тензоров: ( .

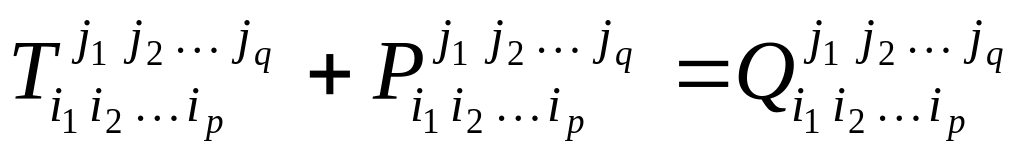2. Умножение тензора на число: ( ).

3. Свертка тензора: (по индексу проводится суммирование).

4. Тензорное умножение: ( ).

Индексы тензора можно поднимать и опускать. Введем метрический тензор . С помощью этого тензора можно опускать индексы: . Числа называются ковариантными координатами вектора, а числа - контрвариантными координатами вектора . С помощью тензора индексы тензора можно поднимать: . Матрицы и связаны соотношением (для симметричных скалярных произведений).

ЗАДАЧИ