
- •Тест № 6 линейные операторы
- •Пусть и – линейные пространства над полем . Из перечисленных утверждений верны следующие:
- •Пусть и – линейные пространства над полем . Из перечисленных утверждений верны следующие:
- •Из перечисленных утверждений справедливы следующие:
- •Из перечисленных утверждений справедливы следующие:
- •Из перечисленных утверждений справедливы следующие:
- •Из перечисленных утверждений справедливы следующие:
- •Из перечисленных утверждений справедливы следующие:
Тест № 6 линейные операторы
1-й вопрос
Пусть
 и
и
 – линейные пространства над полем
– линейные пространства над полем
 .
Из перечисленных утверждений верны
следующие:
.
Из перечисленных утверждений верны
следующие:
а) если
![]() ,
то
,
то
![]() – линейный оператор;
– линейный оператор;
б) если
– линейный оператор, то
![]() ;
;
в) если , то – линейный оператор;
г) если – линейный оператор, то
Верный ответ б), в), г).
Пусть и – линейные пространства над полем . Из перечисленных утверждений верны следующие:
а) если
![]() ,
то
– линейный оператор;
,
то
– линейный оператор;
б) если – линейный оператор, то ;
в) если – линейный оператор, то ;
г) если , то – линейный оператор.
Верный ответ б), в).
Пусть и – линейные пространства над полем . Из перечисленных утверждений верны следующие:
а) если , то – линейный оператор;
б) если , то – линейный оператор;
в) если – линейный оператор, то ;
г) если – линейный оператор, то .
Верный ответ б), в), г).
2-й вопрос
Из перечисленных утверждений справедливы следующие:
а) любой линейный оператор переводит нулевой вектор в нулевой;
б) любой линейный оператор переводит ненулевой вектор в ненулевой;
в) существует линейный оператор, который переводит нулевой вектор в ненулевой;
г) существует линейный оператор, который переводит ненулевой вектор в ненулевой.
Верный ответ а), г).
Из перечисленных утверждений справедливы следующие:
а) любой линейный оператор переводит нулевой вектор в ненулевой;
б) любой линейный оператор переводит ненулевой вектор в ненулевой;
в) существует линейный оператор, который переводит ненулевой вектор в нулевой;
г) существует линейный оператор, который переводит нулевой вектор в нулевой.
Верный ответ в), г).
Из перечисленных утверждений справедливы следующие:
а) любой линейный оператор переводит линейно зависимые элементы в линейно зависимые;
б) любой линейный оператор переводит линейно зависимые элементы в линейно независимые;
в) существует линейный оператор переводит линейно зависимые элементы в линейно зависимые;
г) существует линейный оператор, который переводит линейно независимые элементы в линейно зависимые;
Верный ответ а), в), г).
Из перечисленных утверждений справедливы следующие:
а) любой линейный оператор переводит линейно независимые элементы в линейно независимые;
б) любой линейный оператор переводит линейно независимые элементы в линейно зависимые;
в) существует линейный оператор, который переводит линейно зависимые элементы в линейно независимые;
г) существует линейный оператор, который переводит любые линейно независимые элементы в линейно независимые.
Верный ответ г).
Из перечисленных утверждений справедливы следующие:
а) любой линейный оператор переводит линейно зависимые элементы в линейно зависимые;
б) любой линейный оператор переводит линейно независимые элементы в линейно независимые;
в) существует линейный оператор переводит линейно зависимые элементы в линейно зависимые;
г) существует линейный оператор, который переводит линейно зависимые элементы в линейно независимые.
Верный ответ а), в).
Из перечисленных утверждений справедливы следующие:
а) любой линейный оператор переводит линейно зависимые элементы в линейно независимые;
б) любой линейный оператор переводит линейно независимые элементы в линейно зависимые;
в) существует линейный оператор, который переводит линейно независимые элементы в линейно зависимые;
г) существует линейный оператор, который переводит любые линейно независимые элементы в линейно независимые.
Верный ответ в), г).
3-й вопрос
На плоскости заданы две системы векторов:
 и
и
 .
Существует линейный оператор, переводящий
первую систему во вторую в следующих
случаях:
.
Существует линейный оператор, переводящий
первую систему во вторую в следующих
случаях:
а)
![]() ,
,
![]() ;
;
б)
![]() ,
,
![]() ;
;
в)
![]() ,
.
,
.
Верный ответ б), в).
На плоскости заданы две системы векторов: и . Существует линейный оператор, переводящий первую систему во вторую в следующих случаях:
а)
![]() ,
,
![]() ;
;
б)
![]() ,
;
,
;
в)
,
![]() .
.
Верный ответ а), в).
На плоскости заданы две системы векторов: и . Существует линейный оператор, переводящий первую систему во вторую в следующих случаях:
а)
![]() ,
;
,
;
б)
![]() ,
;
,
;
в)
![]() ,
.
,
.
Верный ответ а), б).
4-й вопрос
Какая из перечисленных ниже матриц может служить матрицей линейного оператора в некотором базисе пространства
 ?
?
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
 ;
д) таких нет.
;
д) таких нет.
Верный ответ а).
Известно, что линейный оператор
 переводит базис
переводит базис
 в систему векторов
в систему векторов
 .
Тогда матрица этого линейного оператора
в заданном базисе имеет вид:
.
Тогда матрица этого линейного оператора
в заданном базисе имеет вид:
а)
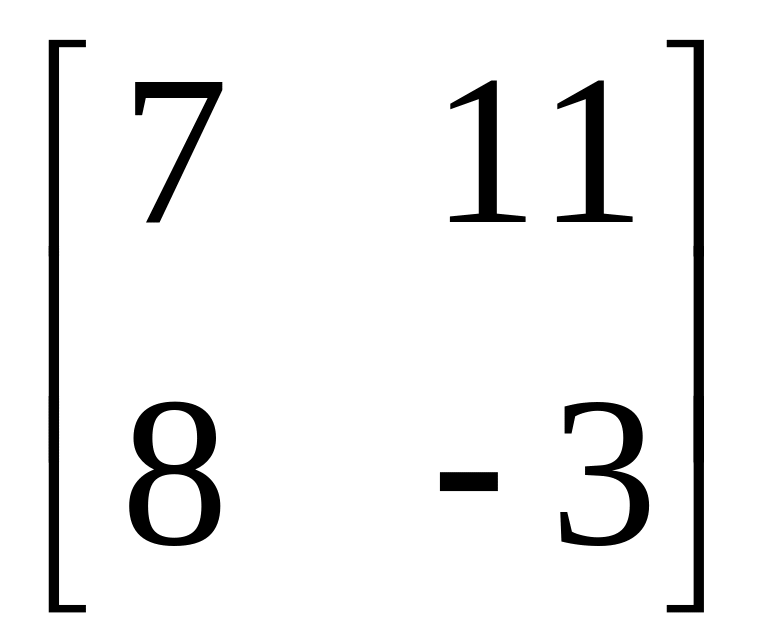 ;
б)
;
б)
 в)
в)
 .
.
Верный ответ б).
Какая из перечисленных ниже матриц может служить матрицей линейного оператора в некотором базисе пространства ?
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
 ;
д) таких нет.
;
д) таких нет.
Верный ответ б).
Известно, что линейный оператор переводит базис в систему векторов
 .
Тогда матрица этого линейного оператора
в заданном базисе имеет вид:
.
Тогда матрица этого линейного оператора
в заданном базисе имеет вид:
а)
 ;
б)
;
б)
 в)
в)
 .
.
Верный ответ в).
5-й вопрос
Если
 и
и
 – матрицы линейного оператора
– матрицы линейного оператора
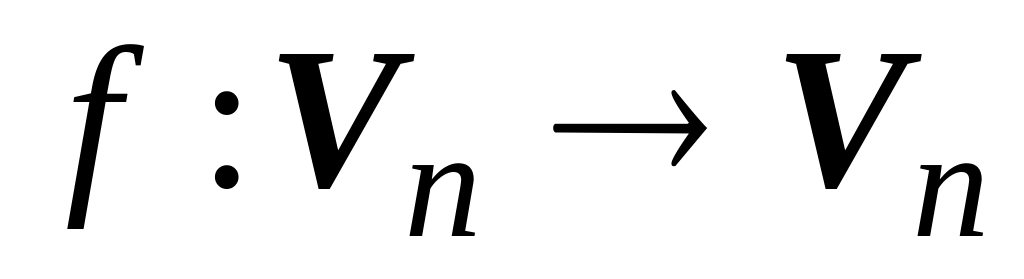 в базисах
в базисах
 и
и
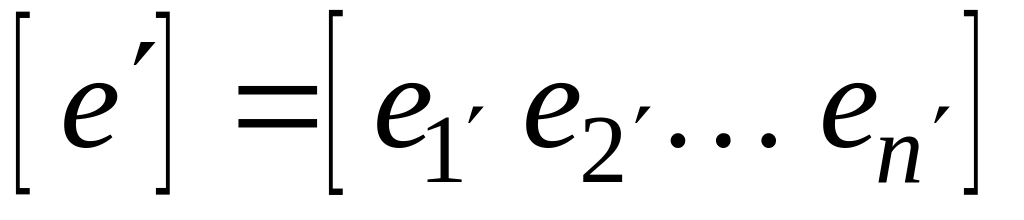 соответственно,
соответственно,
 – матрица перехода от первого базиса
ко второму,
– матрица перехода от первого базиса
ко второму,
 – обратная к ней, то справедливы
следующие формулы:
– обратная к ней, то справедливы
следующие формулы:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Верный ответ б), в).
Если и – матрицы линейного оператора в базисах и соответственно, – матрица перехода от первого базиса ко второму, – обратная к ней, то справедливы следующие формулы:
а)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Верный ответ а), б).
Если и – матрицы линейного оператора в базисах и соответственно, – матрица перехода от первого базиса ко второму, – обратная к ней, то справедливы следующие формулы:
а)
![]() ;
б)
;
в)
;
б)
;
в)
![]() ;
г)
.
;
г)
.
Верный ответ а), г).
6-й вопрос
Если и – матрицы линейного оператора в базисах и соответственно, – матрица перехода от первого базиса ко второму, – обратная к ней, то справедливы следующие формулы:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Верный ответ в).
Если и – матрицы линейного оператора в базисах и соответственно, – матрица перехода от первого базиса ко второму, – обратная к ней, то справедливы следующие формулы:
а)
;
б)
![]() ;
в)
.
;
в)
.
Верный ответ а), в).
Если и – матрицы линейного оператора в базисах и соответственно, – матрица перехода от первого базиса ко второму, – обратная к ней, то справедливы следующие формулы:
а)
;
б)
![]() ;
в)
.
;
в)
.
Верный ответ а).
7-й вопрос
Если – матрица линейного оператора в некотором базисе,
 и
и
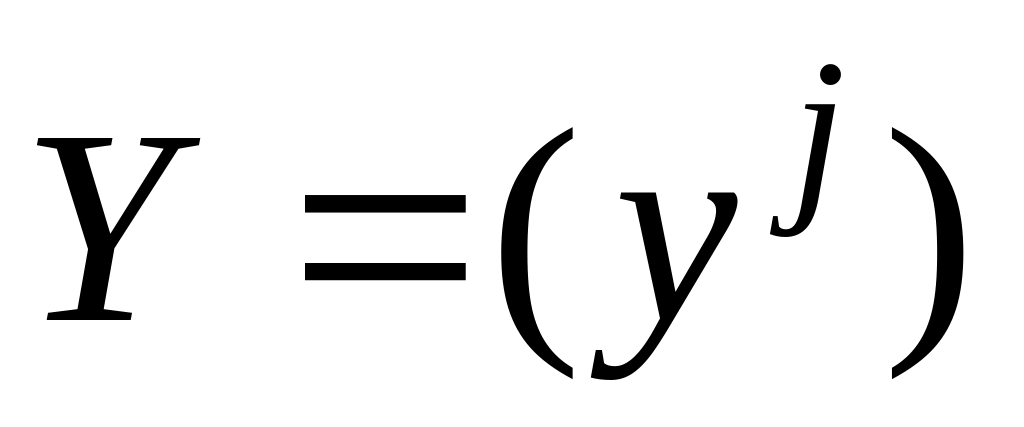 – координатные столбцы векторов
– координатные столбцы векторов
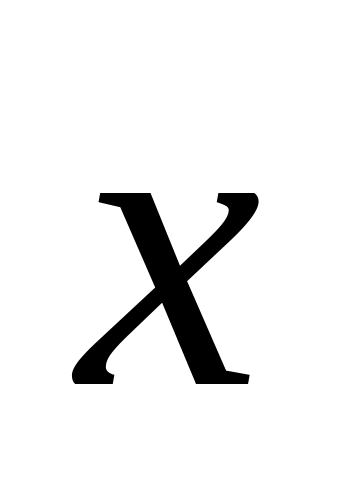 и
и
 соответственно, то справедливы следующие
формулы:
соответственно, то справедливы следующие
формулы:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Верный ответ в).
Если – матрица линейного оператора в некотором базисе, и – координатные столбцы векторов и соответственно, то справедливы следующие формулы:
а)
;
б)
;
в)
![]() .
.
Верный ответ б).
Если – матрица линейного оператора в некотором базисе, и – координатные столбцы векторов и соответственно, то справедливы следующие формулы:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Верный ответ б), в).
Если – матрица линейного оператора в некотором базисе, и – координатные столбцы векторов и соответственно, то справедливы следующие формулы:
а)
;
б)
![]() ;
в)
;
г)
;
в)
;
г)
![]() .
.
Верный ответ а), в).
Если – матрица линейного оператора в некотором базисе, и – координатные столбцы векторов и соответственно, то справедливы следующие формулы:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
г)
.
;
в)
;
г)
.
Верный ответ в), г).
8-й вопрос
В базисе пространства
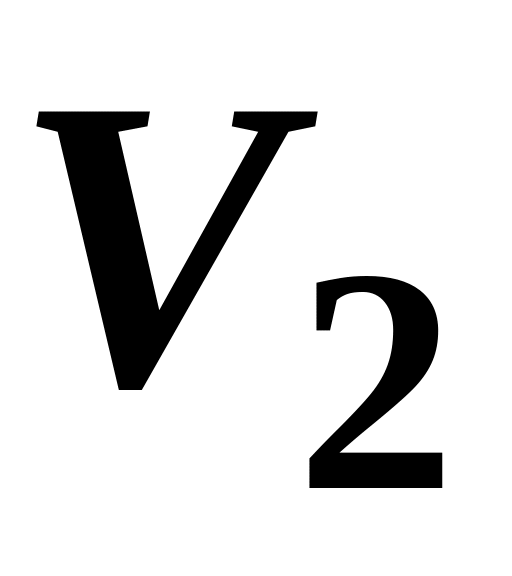 линейный оператор
задан матрицей
линейный оператор
задан матрицей
 ,
а линейный оператор
,
а линейный оператор
 – матрицей
– матрицей
 .
В том же базисе линейный оператор
.
В том же базисе линейный оператор
 задается матрицей:
задается матрицей:
а)
 ;
б)
;
б)
 ;
в)
;
в)
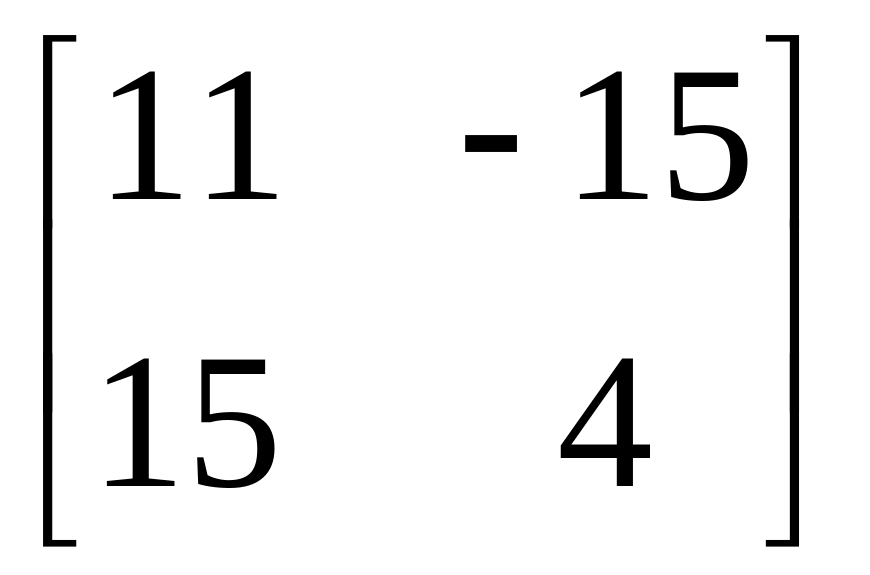 ;
г)
;
г)
 .
.
Верный ответ а).
В базисе пространства линейный оператор задан матрицей , а линейный оператор – матрицей . В том же базисе линейный оператор
 задается матрицей:
задается матрицей:
а) ; б) ; в) ; г) .
Верный ответ б).
В базисе пространства линейный оператор задан матрицей , а линейный оператор – матрицей .В том же базисе линейный оператор
 задается матрицей:
задается матрицей:
а) ; б) ; в) ; г) .
Верный ответ в).
В базисе пространства линейный оператор задан матрицей , а линейный оператор – матрицей .В том же базисе линейный оператор
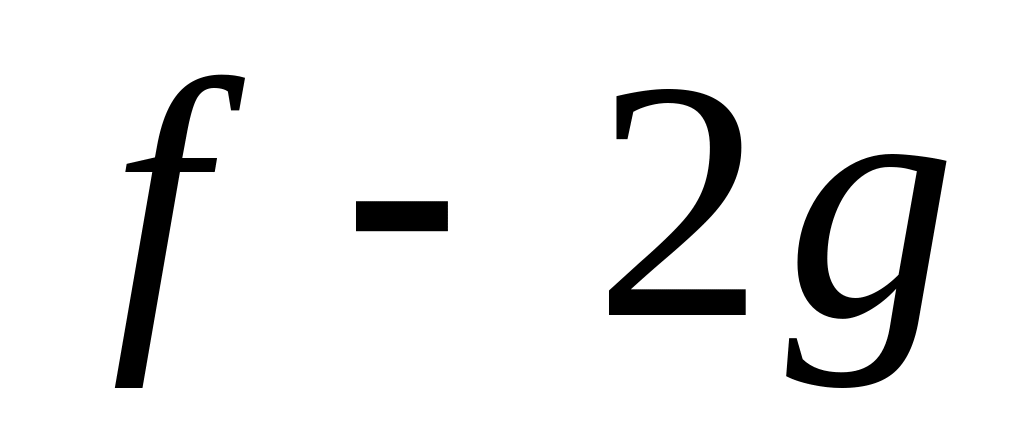 задается матрицей:
задается матрицей:
а) ; б) ; в) ; г) .
Верный ответ г).
9-й вопрос
В базисе пространства линейный оператор задан матрицей
 ,
а линейный оператор
– матрицей
,
а линейный оператор
– матрицей
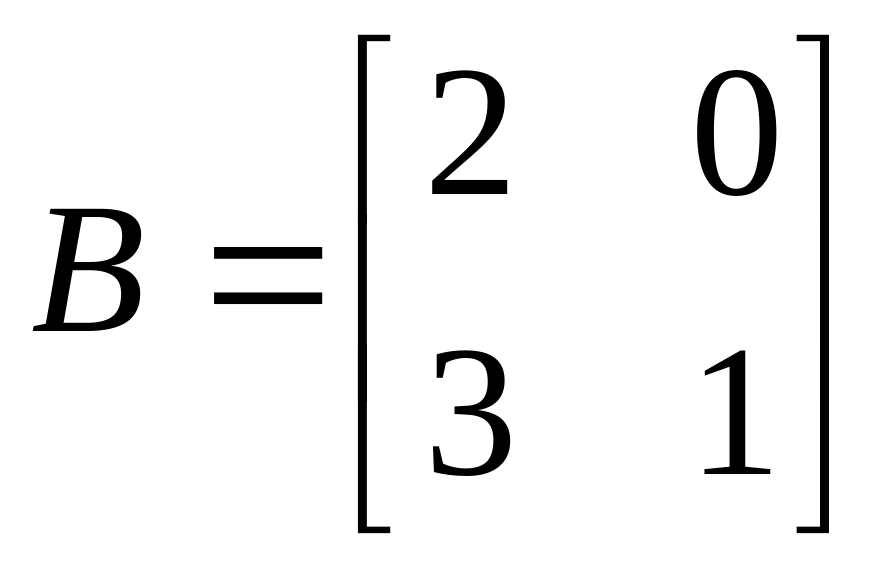 .В
том же базисе линейный оператор
.В
том же базисе линейный оператор
 задается матрицей:
задается матрицей:
а)
 ;
б)
;
б)
 ;
в) другой ответ.
;
в) другой ответ.
Верный ответ а).
В базисе пространства линейный оператор задан матрицей , а линейный оператор – матрицей .В том же базисе линейный оператор
 задается матрицей:
задается матрицей:
а) ; б) ; в) другой ответ.
Верный ответ б).
10-й вопрос
В базисе пространства линейный оператор задан матрицей
 .
Этот оператор является невырожденным,
если
совпадает с матрицей:
.
Этот оператор является невырожденным,
если
совпадает с матрицей:
а)
 ;
б)
;
б)
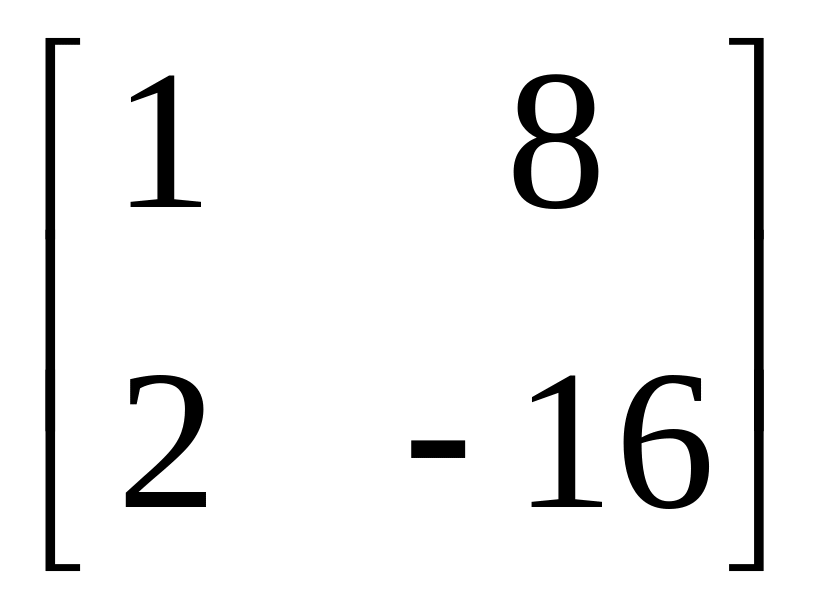 ;
в)
;
в)
 ;
г)
;
г)
 .
.
Верный ответ б), в).
В базисе пространства линейный оператор задан матрицей . Этот оператор является взаимно однозначным, если совпадает с матрицей:
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
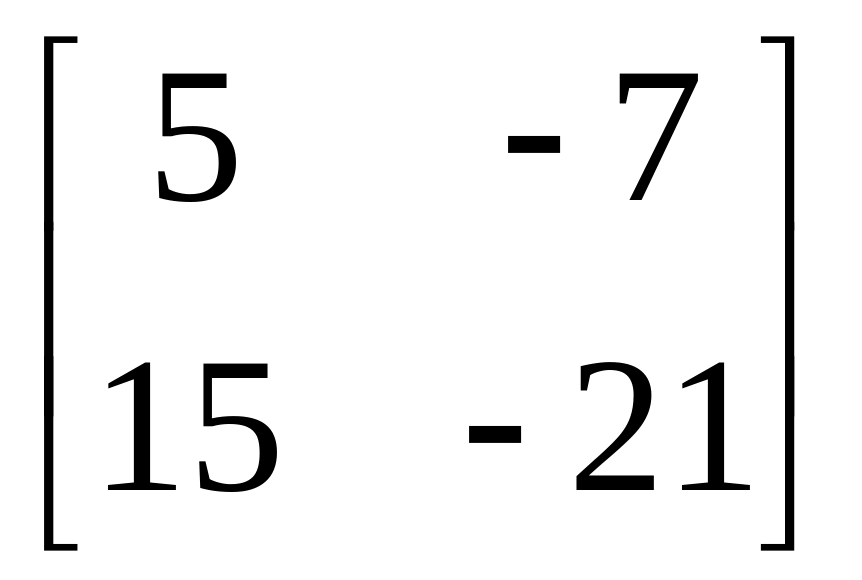 .
.
Верный ответ а), в).
В базисе пространства линейный оператор задан матрицей
 .
В том же базисе обратный оператор имеет
матрицу:
.
В том же базисе обратный оператор имеет
матрицу:
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
 .
.
Верный ответ б).
В базисе пространства линейный оператор задан матрицей
 .
В том же базисе обратный оператор имеет
матрицу:
.
В том же базисе обратный оператор имеет
матрицу:
а)
 ;
б)
;
б)
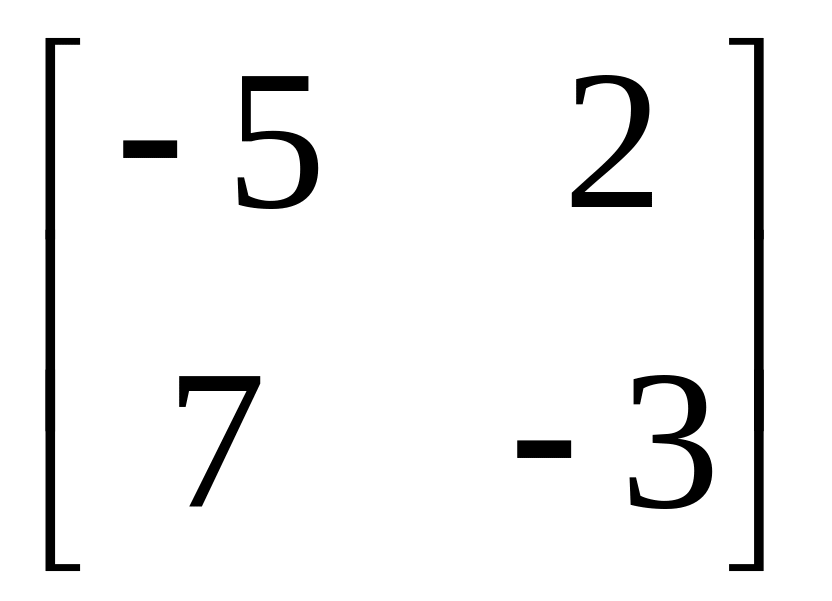 ;
в)
;
в)
 ;
г)
;
г)
 .
.
Верный ответ в).
В базисе пространства линейный оператор задан матрицей
 .
В том же базисе обратный оператор имеет
матрицу:
.
В том же базисе обратный оператор имеет
матрицу:
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
 .
.
Верный ответ г).
