Неопределенный интеграл

Неопределенный интеграл

Пусть f(x) определена на (a,b), тогда F(x) называется первообразной, если во всех точках F’(x)=f(x).

Пусть F1(x), F2(x) первообразные f(x) на (a,b), тогда F1(x)-F2(x)=const

Док-во:

(F1(x)-F2(x))’=f(x)-f(x)=0

по формуле Лагранжа F1(x)-F2(x)=const

Совокупность всех первообразных f(x) называется неопределенным интегралом.

Св-ва:

1^о , ,

2^о ,

3^о

4^о

Методы интегрирования

Метод замены переменной (подстановки)

, , , ,

Гиперболические функции

sh x=(e^x-e^-x)/2, ch x=(e^x+e^-x)/2, tg x=sh x/ch x, ch² x-sh² x=1, ch 2x=2sh² x+1=2ch² x-1=ch² x+sh² x, sh 2x=2shxchx

(sh x)’=ch x, (ch x)’=sh x

Интегрирование по частям

Если u,v дифференцируемые функции, то

Док-во:

(uv)’=u’v+uv’, , uv=,

Интегрирование дробно-рациональных функций.

Интеграл от дробно-рациональной функции является элементарной функцией.

Пусть дана правильная рациональная дробь P(x)/(x-a)ⁿQ(x), n>=1, тогда существует такое число А и P1(x)

P(x)/(x-a)ⁿQ(x)=A/(x-a)ⁿ+ P1(x)/(x-a)^n-1Q(x)

Док-во:

A=P(a)/Q(a)

P(x)/ (x-a)ⁿQ(x)-A/(x-a)ⁿ=(P(x)-AQ(x))/(x-a)ⁿQ(x)=(P(a)-P(a)/Q(a)*Q(x))/(x-a)ⁿQ(x)=∞,

(P(x)-AQ(x))/(x-a)ⁿQ(x)=(x-a)P1(x)/(x-a)ⁿQ(x)=P1(x)/(x-a)^n-1Q(x)

Пусть дана правильная рациональная дробь P(x)/(x²+px+q)ⁿQ(x), n>=1, тогда существует такое число А,B и P1(x)

Ax+B/x²+px+q + P1(x)/(x²+px+q)^n-1Q(x)

Интегрирование иррациональных и транцедентных функций

=

Дифференциальный бином

Пусть р-целое n-рациональное (k,l-целые, l-положит) n=k/l x=t^l

Пусть (m+1)/n целое z=xⁿ x=z^1/x dx=1/n*z^(1/n-1)dz

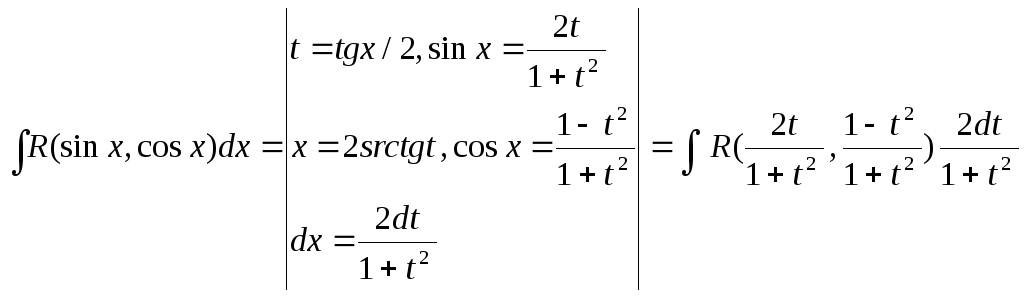
Пусть целое p=k/l ax^-n+b=t^l