2.2.2 Методы получения суждения от эксперта

В различных способах проведения опроса могут быть использованы следующие методы получения суждения от эксперта:

1. методы разбиения на множества;

2. методы ранжирования;

3. методы получения численных оценок.

Метод разбиения на множества

Метод разбиения на множества используется, если некоторый признак необходимо измерить в номинальной шкале, т.е. по заранее четко сформулированному признаку предлагается разделить объекты на множества по одинаковой степени интенсивности проявления указанного признака. Например, необходимо разбить 5 специалистов на три множества – «специалисты-теоретики», «специалисты-практики» и «универсальные специалисты». Вариант ответа от эксперта: специалисты-теоретики - Иванов, Петров, специалисты-практики – Соколов, универсальные специалисты - Сидоров, Кузнецов. Обычно множества описываются таким образом, чтобы они не пересекались.

В номинальной шкале задано только отношение тождества. Каждый оцениваемый объект либо относится к некоторому множеству, либо нет. Объекты нельзя сравнивать между собой по признакам «лучше-хуже», «больше-меньше», никакие арифметические действия в этой шкале также не выполняются.

Методы ранжирования

Методы ранжирования используются, если объекты упорядочиваются, оцениваются в ранговой (порядковой, ординальной) шкале. При этом каждому из них можно поставить в соответствие число, называемое рангом.

В ординальной шкале задано отношение «больше-меньше» («лучше-хуже»), но никаких арифметических действий также нельзя производить (нельзя ответить на вопрос, на сколько лучше, или во сколько раз лучше).

Обычно первый ранг присваивается наиболее предпочтительному объекту, второй – следующему и т.д. Если эксперт не может дифференцировать по предпочтительности некоторые объекты и присваивает им одинаковые ранги, для них рассчитывают так называемые стандартизированные ранги, которые определяются, как среднее арифметическое мест, занимаемых объектами с одинаковыми рангами.

Рассмотрим упрощенный пример. Пусть требуется упорядочить 5 способов усовершенствовать состав аппарата и организационную структуру управления некоторым предприятием:

А) сменить генерального директора на г-на Смирнова;

Б) сменить генерального директора на г-на Колосова;

В) подчинить отдел сбыта непосредственно генеральному директору;

Г) ввести в штат дополнительного секретаря генерального директора;

Д) сменить начальника отдела сбыта.

Предположим, эксперт Петров считает наилучшими изменения в отделе сбыта, добавление секретаря ему представляется бессмысленным, а варианты смены директора он считает равноценными и не может определить, какому из них присвоить 3-й, а какому - 4-й ранг. Тогда он предлагает следующее ранжирование (таблица 6):

Таблица 6 – Индивидуальная ранговая оценка (эксперт Петров)

Объекты (способы)	А	Б	В	Г	Д
Ранги	3	3	2	4	1
Стандартизированные ранги	3,5	3,5	2	5	1

Способам А и Б здесь присвоен стандартизированный ранг (3 + 4)/2 = 3,5.

П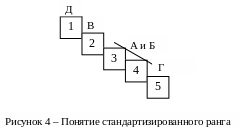 онятие стандартизированного ранга можно проиллюстрировать следующим образом. Представьте себе лестницу («пьедестал») из пяти ступенек, на которых надо разместить пять объектов оценивания – по одному на каждой. Первые две ступеньки займут Д и В, поскольку нет сомнений, что у объекта Д – первое место, а у В – второе. А вот на следующее место «претендуют» сразу два объекта: А и Б. Но поместить их на одну ступень нельзя: два объекта должны занять две ступени – третью и четвертую. Следовательно, номера этих ступеней усредняются (рис. 4). Объект Г занимает оставшуюся, пятую ступень.

Стандартизированные ранги могут быть присвоены и более чем двум объектам. Допустим, эксперт Сидоров сформулировал следующие предпочтения (таблица 7):

Таблица 7 – Индивидуальная ранговая оценка (эксперт Сидоров)

Объекты (способы)	А	Б	В	Г	Д
Ранги	2	2	1	2	1
Стандартизированные ранги	4	4	1,5	4	1,5

Для способов А, Б и Г стандартизированный ранг подсчитан как (3 + 4 + 5)/3 = 4 (рис.5).

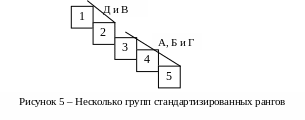
Расчет стандартизированных рангов позволяет сравнивать ранговые оценки различных экспертов между собой и формировать групповое ранжирование. В противном случае такое сравнение было бы затруднительным (в самом деле, последнее место для Петрова соответствует четвертому рангу, для Сидорова – второму, в результате, чем хуже эксперт дифференцирует альтернативы, тем выше ранг у оцененных им объектов).

В методах ранжирования можно выделить:

а) метод непосредственного упорядочения (рассмотренная выше процедура). Его удобно использовать для упорядочения небольшого количества объектов. Если их много, используют другие методы, такие как

б) двоичное сравнение – при котором объекты сравниваются попарно. Результаты записываются в виде квадратной матрицы, элементы которой х_ij принимают значения 1 или 0:

(4)

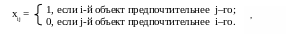
где n – число сравниваемых объектов.

Диагональ матрицы не заполняется (объект не сравнивается сам с собой).

Если экспертам разрешается не дифференцировать некоторые объекты, формула может иметь вид:

(5)

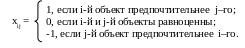
В общем случае каждая пара объектов сравнивается дважды, что позволяет получить более достоверную информацию за счет предоставления эксперту возможности скорректировать свое мнение. Осуществляется n*(n - 1) сравнений.

Иногда с целью уменьшения объема работ осуществляют частичное двоичное сравнение, когда каждая пара объектов сравнивается только один раз (пользуются тем фактом, что x_ij = -x_ji).

Переход к ранговой оценке осуществляют следующим образом: суммируют числа по строкам матрицы, и 1-й ранг получает объект с наибольшей суммой, следующий – 2-й ранг и т.д.

Например, при применении частичного двоичного сравнения к оценкам Петрова матрица примет следующий вид (таблица 8):

Таблица 8 – Частичное двоичное сравнение

	А	Б	В	Г	Д	Сумма	Ранг	Станд. ранг
А		0	-1	1	-1	-1	3	3,5
Б	0		-1	1	-1	-1	3	3,5
В	1	1		1	-1	2	2	2
Г	-1	-1	-1		-1	-4	4	5
Д	1	1	1	1		4	1	1

Однако, если применить процедуру двоичного сравнения полностью, может возникнуть, например, ситуация, когда, повторно сравнивая кандидатуры Смирнова и Колосова, Петров все же решит, что Колосов предпочтительнее, что приведет к следующему ранжированию (таблица 9):

Таблица 9 – Полное двоичное сравнение

	А	Б	В	Г	Д	Сумма	Ранг
А		0	-1	1	-1	-1	4
Б	1		-1	1	-1	0	3
В	1	1		1	-1	2	2
Г	-1	-1	-1		-1	-4	5
Д	1	1	1	1		4	1