2.3.3 Оценка согласованности мнений экспертов

В п. 2.1.1 был рассмотрен пример, когда один из двух метеорологов оценивает вероятность дождя в 0,1, а другой – 0,9. Принимать групповую оценку 0,5 (простое среднее) при таком сильном расхождении во мнениях очевидно бессмысленно, поскольку кто-то из экспертов явно исходит в своей оценке из неверных предпосылок. Такая обобщенная оценка не является значимой, не пригодна для использования на практике.

Итак, значимость полученной групповой оценки в большой степени определяется согласованностью индивидуальных оценок экспертов. В связи с этим встает вопрос об определении приемлемой меры согласованности, а также о разработке методов и процедур повышения согласованности мнений экспертов, если она недостаточна.

Согласованность оценок в номинальной шкале

Для оценок, полученных в номинальной шкале, вопрос об оценке согласованности можно решить достаточно просто, например, путем различных модификаций (усилений) правила большинства. Например, можно заранее установить, что если ни за какое мнение не проголосовало большинство как минимум в 3/4 голосов, то такая согласованность считается недостаточной, соответственно, оценка не является значимой, необходимо провести повторную экспертизу.

Согласованность численных оценок

Для оценки согласованности численных оценок рассчитываются различные статистические величины - дисперсия, СКО, коэффициент вариации. При этом, как правило, рассчитывается несмещенная оценка дисперсии, т.е. оценки экспертов рассматриваются, как случайная выборка^*:

(7)

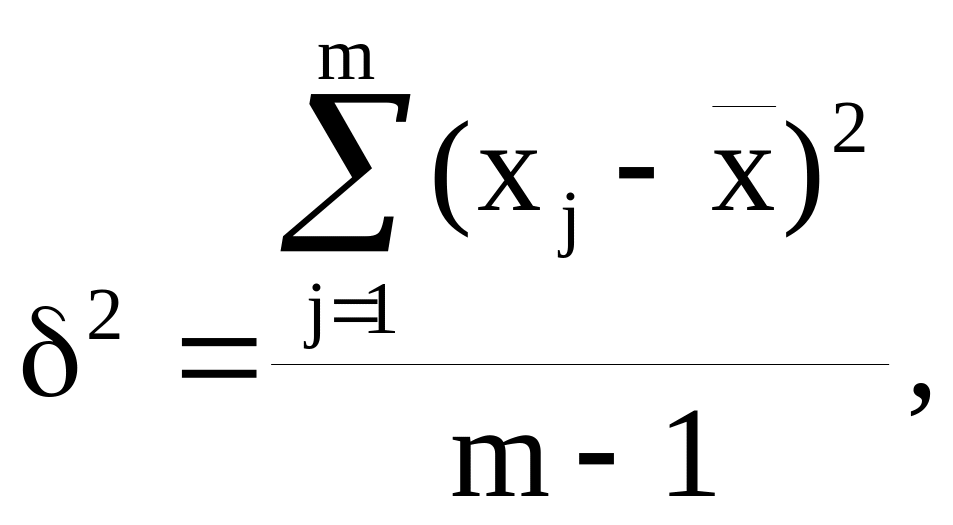
где - дисперсия,

x_j – оценка, данная j–м экспертом,

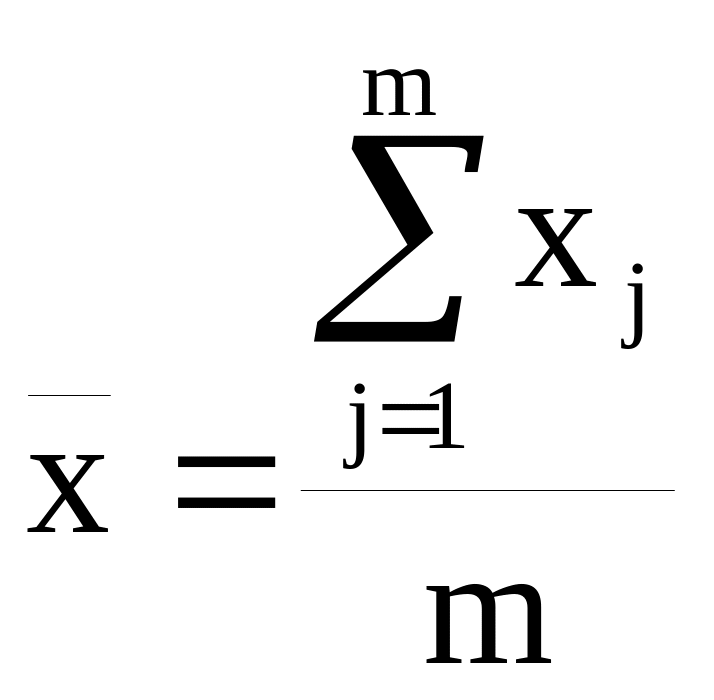– среднее арифметическое оценок, данных различными экспертами,

m - число экспертов.

С

(8)

реднее квадратическое отклонение (СКО), в отличие от дисперсии, является величиной, имеющей те же единицы измерения, что и сама оценка (дисперсия измеряется в квадратах этих единиц):

где - среднее квадратическое отклонение.

Если оценки стоимости некоторого проекта имеют СКО 4 тыс. руб. – это много или мало? Если порядок оценок составляет тысячи или десятки тысяч, то достаточно много, разброс оценок большой; а вот если сотни тысяч и миллионы – то, напротив, он не так велик. Поэтому необходимо рассчитать также коэффициент вариации - относительный показатель, не имеющий единиц измерения, позволяющий сравнивать среднеквадратическое отклонение со средней оценкой (оценить, велико это отклонение или мало в масштабах данных оценок):

(9)

где - коэффициент вариации.

Мнения экспертов можно считать согласованными, если значения этих показателей не выходят за рамки предварительно заданных граничных значений, например, коэффициент вариации составляет не более 0,1.

Например, пусть трем экспертам предложено оценить по трехбалльной шкале экономическую эффективность одной из альтернатив (таблица 18). Граничное значение коэффициента вариации примем равным 0,25.

Таблица 18 – Оценка согласованности численных оценок (вспомогательные расчеты для нахождения коэффициента вариации)

Эксперт	Оценка
Иванов	2	1/3	1/9
Петров	2	1/3	1/9
Сидоров	3	- 2/3	4/9
Сумма	7		2/3

= 7/3 = 2 1/3; = (2/3) / 2 = 1/3; 0,58; 0,25. Поскольку граничное значение не превышено, будем считать оценки согласованными

Другой метод оценки согласованности – использование статистического критерия (“хи-квадрат”).

Предполагается, что полностью несогласованные оценки распределены равномерно по всей шкале, т.е. на каждую градацию приходится равное количество оценок m/L, где m – число экспертов, L - число градаций в используемой шкале. Например, если 15 экспертов оценивают объект по 3-балльной шкале, то равномерное распределение соответствует 5 оценкам в каждой градации (15/3 = 5), т.е. оно имеет место, если пять экспертов поставили 1 балл, пять экспертов – 2 балла, и 3 балла тоже поставили 5 экспертов (всего 15 оценок).

На самом деле в каждую j–ю градацию попало m_j оценок ( ). Например, предположим, никто не поставил 1 балл что (m₁=0), 10 экспертов поставили 2 балла (m₂=10), и 5 экспертов поставили 3 балла (m₃=5). Подсчитаем сумму квадратов относительных отклонений частот m/L от частот m_j - 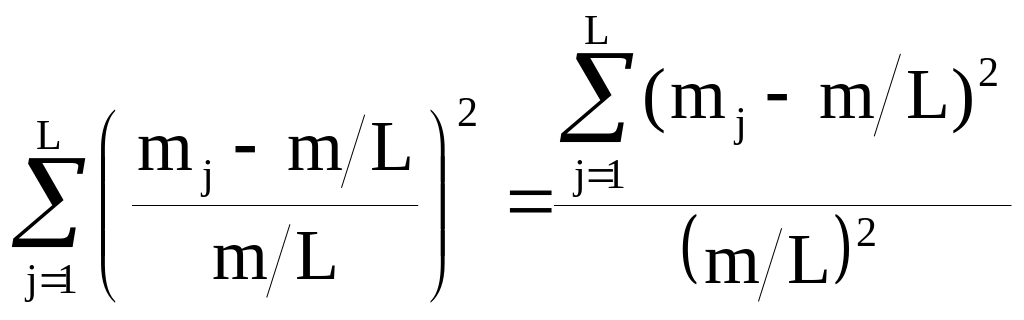. Чем эта величина больше, тем с большей уверенностью можно утверждать, что оценки согласованы (их частоты отличаются от частот при равномерном распределении). Данная величина подчиняется -распределению с числом степеней свободы L-1^*.

С некоторой вероятностью рассчитанная величина может оказаться больше реальной случайно, и тогда мы сделаем неправильный вывод о согласованности оценок. Поэтому задают малое значение этой вероятности, т.е. уровень значимости. Обычно его берут равным 0.05, 0.01 или 0.001, но допустимы и более высокие значения в зависимости от ситуации.

Затем по статистическим таблицам (приложение В) определяют значение при заданном уровне значимости и числе степеней свободы. В данном примере при двух степенях свободы =5.991. Если полученное расчетное значение будет больше табличного, то гипотеза о равномерном распределении оценок будет отвергнута, и оценки можно считать согласованными. В противном случае оценки считают несогласованными.

В данном примере = ((0-5)² + (10-5)² + (5-5)²)/5² = (25 + 25 + 0)/25 = 2 < 5.991. Более того, в статистической таблице для -распределения с двумя степенями свободы значение 2 находится примерно в середине таблицы, т.е. соответствует уровню значимости 0.5. К сожалению, это не дает возможности отвергнуть гипотезу о равномерном распределении – она может оказаться верной или неверной почти с равной вероятностью. Чтобы сделать более уверенный вывод, необходимо увеличить согласованность оценок.

Оба рассмотренных выше метода могут быть использованы только при оценке объекта по одному фактору. Если объект оценивается по нескольким факторам (по n факторам), то для измерения согласованности между оценками ДВУХ экспертов (или между отдельным экспертом и групповым мнением) рассчитывают евклидово расстояние между ними, рассматривая каждую оценку, как точку в n–мерном пространстве:

(10)

где r – расстояние между оценками двух экспертов;

n – число факторов;

x_i – оценка i–го фактора одним из экспертов;

y_i - оценка i–го фактора другим экспертом.

Предположим, например, что эксперты оценивают не только экономическую эффективность метода, но также и его социальную эффективность (таблица 19):

Таблица 19 – Оценка согласованности численных оценок через евклидово расстояние

Эксперт	Оценка экономической эффективности	Оценка социальной эффективности	Расстояние между оценками
			Иванов	Петров	Сидоров
Иванов	2	3		2	1
Петров	2	1	2		2.2
Сидоров	3	3	1	2.2
Групповая оценка*	2,36	2,36**	0,7	1,4	0,9

Расстояние между оценками Иванова и Петрова составляет = 2. Расстояния между оценками Иванова и Сидорова, Петрова и Сидорова, а также каждого из них и групповой оценкой рассчитаны аналогично.

Из данного примера видно, что мнение Петрова наиболее значительно отличается от мнений двух других экспертов и от группового (расстояние – 1,4), особенно от мнения Сидорова (расстояние – 2,2), мнения же Иванова и Сидорова наиболее близки друг к другу (расстояние – 1). Иванов ближе всех к групповому мнению (расстояние – 0,7). Поскольку оцениваются всего два фактора, данный пример можно пояснить рисунком 6, на котором расстояния между оценками представлены наглядно.

Е сли факторов более 2-3, оценить близость оценок визуально становится невозможно, и без расчета расстояний обойтись уже не удается. Для таких расчетов рекомендуется использовать программные средства, так как с ростом числа экспертов (m) число расстояний, которые необходимо подсчитать, существенно увеличивается (m*(m-1)/2).

С использованием данного показателя экспертов можно разбивать на группы, мнения внутри которых отличаются более высокой согласованностью по сравнению со всей групповой оценкой. Изучением таких групп занимается кластерный анализ (здесь подробно не рассматривается).

Отметим, что при использовании евклидова расстояния для измерения согласованности различные показатели будет лучше перевести в балльные шкалы с равным числом градаций, в противном случае разница в масштабе может существенно повлиять на величину расстояния. Измерить согласованность индивидуальных оценок через расстояние можно различными способами, например, путем вычисления среднего попарного расстояния, либо среднего расстояния до групповой оценки (их значения должны быть не больше заранее заданных).

Будем считать оценки в данном примере согласованными, если среднее попарное расстояние не превысит 2, а до групповой оценки – 1. Среднее попарное расстояние равно (2 + 1 + 2.2) / 3 = 1.73 < 2. Среднее расстояние до групповой оценки: (0.7 + 1.4 + 0.9) / 3 = 1. Следовательно, оценки можно считать согласованными.