Обобщение численных оценок

Для обобщения численных оценок используются различные средние, – обычно это простое или взвешенное среднее, медиана и мода.

Моду и медиану обычно используют, если экспертов много, и различия в их компетентности не учитываются.

Рассмотрим пример. Пусть требуется оценить те же 5 способов совершенствования управления предприятием в 3-балльной шкале. Если, по мнению эксперта, применение данного способа не принесет пользы, он оценивает его в 1 балл, если некоторый эффект будет иметь место – 2 балла, если эффект будет значительным – 3 балла. Результаты опроса и расчетов приведены в таблице 14:

Таблица 14 – Формирование групповой численной оценки

Способы Эксперты	А	Б	В	Г	Д	Коэффициент компетентности
Иванов	2	2	2	1	3	0,36
Петров	2	2	3	2	3	0,2
Сидоров	3	3	2	1	1	0,44
Mo	2	2	2	1	3
Me	2	2	2	1	3
Среднее	2,44	2,44	2,2	1,2	2,12

Расчет средней взвешенной оценки рассмотрим на примере способа А: 2*0,36 + 2*0,2 + 3*0,44 = 2,44. Мода и медиана для всех способов совпадают, поскольку экспертов всего трое, и если на какую-то из оценок выпадает 2 мнения из трех (большинство), то она является одновременно и модой, и мнением того эксперта, который находится в середине ряда из трех экспертов, проранжированных по своим оценкам. Отметим, что если округлить средние взвешенные до целых, то здесь и они во всех случаях совпадают с другими средними, за исключением способа Д. Для него Мо = Ме = 3, а среднее взвешенное равно 2. Т.е., если учитывать более высокую компетентность Сидорова, эффект от замены начальника отдела сбыта не следует все же считать очень значительным.

Стоит отметить, что средневзвешенная оценка будет получена в непрерывной шкале. Если необходимо перевести ее в дискретную, можно заранее оговорить способ округления, но обычно это не делается.

Обобщение ранговых оценок

Построение групповой оценки в случае ранжирования представляет несколько большую сложность^*. Рассмотрим несколько методов обобщения ранговых оценок:

1. По числу первых мест – согласно этому методу наилучший ранг имеют те объекты, которые большинство экспертов поместило на первые места в ранжировании.

Например, пусть от экспертов получено ранжирование для тех же 5 способов совершенствования управления предприятием (таблица 15). Групповую оценку получим в несколько этапов. Вначале подсчитаем, сколько экспертов проголосовало за то, чтобы присвоить способу 1-й ранг, или 1-е место. За это мнение проголосовало по одному эксперту для способов А и Д. Следовательно, 1-й ранг в групповой оценке должен быть присвоен одному из этих способов. Уточним теперь, сколько экспертов присвоили способам ранг 1.5 (следующая по величине из полученных оценок). Этот ранг также был получен дважды – по одному разу для объектов В и Д. Следовательно, 1-й ранг в групповом ранжировании следует присвоить способу Д (он имеет оценки 1 и 1.5), 2-й – способу А (так как он имеет оценку 1) и 3-й – способу В (так как он имеет оценку 1.5). Осталось упорядочить способы Б и Г. Теперь надо определить, сколько экспертов и для каких из этих способов проголосовали за 2-е место. Такая оценка была получена только для способа Б, следовательно, ему следует присвоить 4-й ранг, а оставшемуся способу Г – 5-й ранг.

2. По сумме рангов – наилучший ранг получают те объекты, для которых сумма рангов, полученных от всех экспертов, является наименьшей. Этот метод может быть использован в различных модификациях.

Для того же примера (таблица 15) простое суммирование рангов не позволяет сравнить между собой способы В и Д, и они получают одинаковый стандартизированный ранг 1,5.

Однако, можно уточнить полученную оценку по числу первых мест, - поскольку из этих двух способов способ Д получил от одного из экспертов 1-е место, ему присваивают ранг 1, а способу В – ранг 2.

3. Другой способ обобщения оценок – суммирование квадратов рангов (таблица 15). Расчеты поясним на примере способа Д: 1² + 1.5² + 4² = 1 + 2.25 + 16 = 19.25. С использованием этого метода 1-й ранг будет присвоен способу В, а 2-й – способу Д. Здесь сыграло свою роль число последних мест, а именно тот факт, что одним из экспертов способу Д был присвоен предпоследний, 4-й ранг, что значительно увеличило сумму квадратов. Что касается способа В, то хотя никто и не сопоставил этому способу 1-й ранг, но никто и не оценил его слишком низко.

Таблица 15 – Формирование групповой ранговой оценки

Способы Эксперты	А	Б	В	Г	Д
	Индивидуальное ранжирование
Иванов	3,5	3,5	2	5	1
Петров	4	4	1,5	4	1,5
Сидоров	1	2	3	5	4
	По числу первых мест
№ места	Количество голосов
1	1				1
1.5			1		1
2		1
Ранг	2	4	3	5	1
	По сумме рангов
Сумма рангов	8,5	9,5	6,5	14	6,5
Ранг	3	4	1,5	5	1,5
	Уточнение по числу первых мест
Ранг	3	4	2	5	1
	По сумме квадратов рангов
Сумма квадратов рангов	29,25	32,25	15,25	66	19,25
Ранг	3	4	1	5	2

Из рассмотренного примера видно, что использование четырех различных методов позволяет получить четыре различных упорядочения. Это наглядно иллюстрирует, каким образом рабочая группа, выбирая метод обобщения оценок, может манипулировать результатами опроса. Тем не менее, некоторые выводы могут быть сделаны объективно. В частности, оценки для способов Б и Г совпадают и практически не вызывают сомнений. Способ Д (смена начальника отдела сбыта) в любом случае занимает одно из первых двух мест.

Ни один из рассмотренных методов нельзя использовать в случае неполного ранжирования, когда эксперты сравнивают между собой различное число альтернатив.

Например, пусть по некоторым причинам эксперт Иванов не учитывал при ранжировании способ Б, Петров – способ А, а Сидоров – способы В и Г (возможно, эти альтернативы просто не были доведены до их сведения, либо эксперты посчитали такого рода действия лежащими вне сферы своей компетенции) (таблица 16). Теперь уже не имеет смысла подсчитывать число первых мест, т.к. второе место из четырех альтернатив несравнимо со вторым из трех. Суммировать ранги также нельзя, так как некоторые способы оценивались двумя экспертами, а некоторые – тремя, следовательно, полученные суммы нельзя будет сравнивать. Для такого случая разработан ряд специальных методов, наиболее простым из которых является подсчет среднего арифметического ранга для каждого из сравниваемых объектов.

Средний ранг j–го объекта М_j рассчитывается по формуле:

(6)

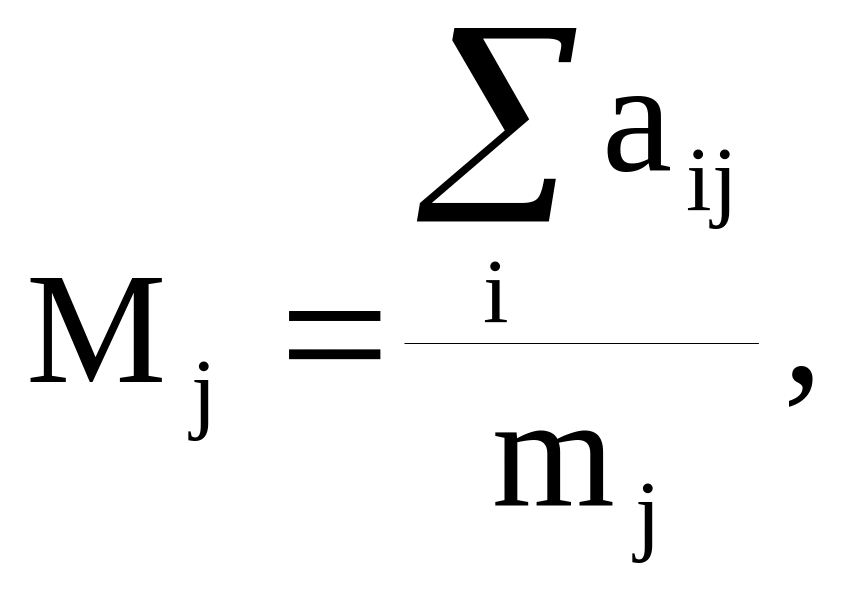
где а_ij – ранг, который i–й эксперт приписывает j–му объекту,

m_j, – число экспертов, которые оценили j–й объект,

n – число объектов.

Таблица 16 – Неполное ранжирование

Способы Эксперты	А	Б	В	Г	Д
	Индивидуальное ранжирование
Петров	3	-	2	4	1
Сидоров	-	3,5	1,5	3,5	1,5
Кузнецов	1	2	-	-	3
Средний ранг	2	2,75	1,75	3,75	1,83
Ранг	3	4	1	5	2

Для данного примера М₁ = (3+1)/2 = 2; М₂ = (3.5+2)/2 = 2,75; и т.д., М₅ = (1 + 1.5 + 3)/3  1,83.