1.4 Наилучший результат выборки

Откуда берутся истинные значения измеряемых величин, относительно которых случайным образом разбро­саны результаты измерений? Чаще всего эти значения неизвестны и в инженерной практике даже не являются необходимыми. Более важным яв­ляются ответы на два вопроса:

Как получить наилучшую оценку из­меряемой величины, располагая некоторым множеством измерений;

Сколько отдельных измерений следует сделать.

Для нормального распределения все инженеры и учёные использу­ют в качестве наилучшей оценки среднее значение:

1.5 Распределение ошибок, отличающееся от нормального

Допустим, произведено 67 измерений с Земли высоты летательного аппарата и построена гистограмма измерений, достаточно близкая к нормальному распределению:

Рис. 7 Гистограмма измерений высоты, распределенных почти нормально вблизи среднего значения.

Расчёт среднеквадратического отклонения для такой выборки, даёт значение:

км.

Вероятная ошибка для такой выборки оказывается равной:

км

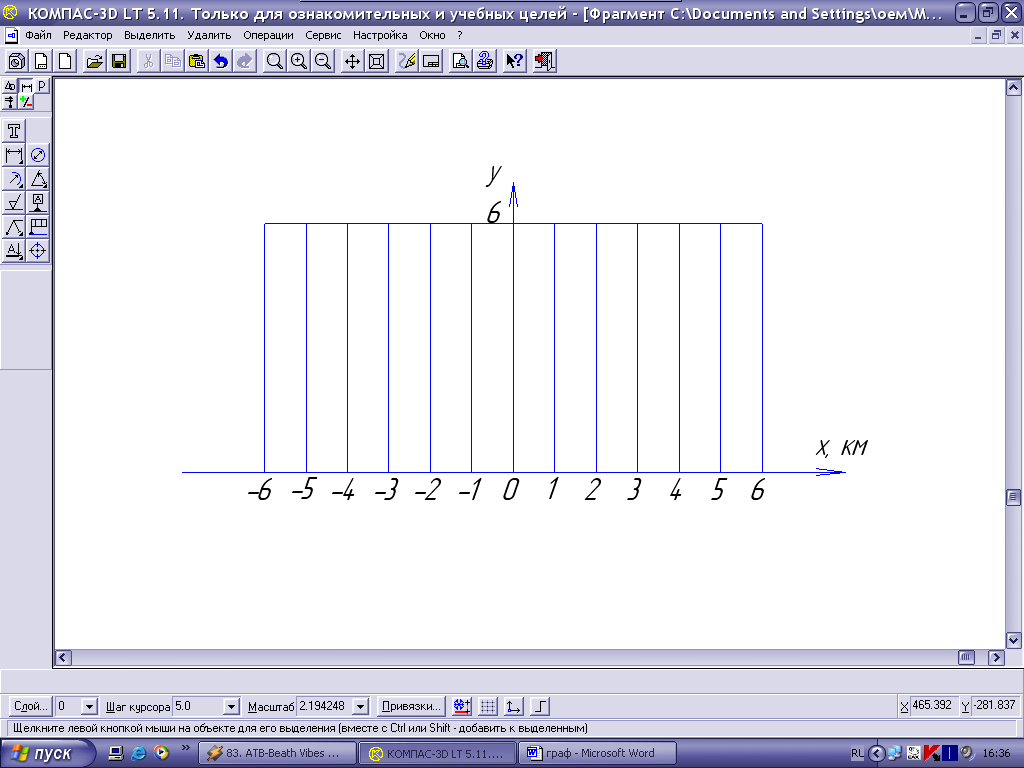Таким образом, в интервал 2,7 км вблизи среднего значения попадает половина измерений. Рассмотрим теперь вместо нормального распреде­ления равномерное распределение в интервале 5,5 км, в котором дол­жны уложиться все 67 измерений:

Рис. 8 Гистограмма измерений высоты, распределенных равновероятно в близи среднего значения.

Для этого равномерного распределения вероятная ошибка также ра­вна 2,7 км, однако если рассчитать среднеквадратичное отклонение, то оно окажется равным 3,2 км, что примерно на 20% меньше значе­ния нормального распределения.

На практике мало, какое распределение так сильно отличается от нормального, как равномерное распределение и, таким образом эти 20% можно считать предельным отличием от значений, полученных для нор­мального распределения. Обычно принимается допущение о нормальности распределения вероятностей, поскольку такое распределение наиболее хорошо изучено математиками.

2. Ошибка и неопределенность эксперимента в целом

В большинстве инженерных экспериментов показания снимаются с нескольких приборов и конечным результатом, является некоторая мате­матическая комбинация этих показаний. Будем считать, что показания отдельных приборов имеют случайную ошибку с нормальным распределени­ем. Чаще всего комбинация показаний представляется в виде произве­дения либо частного: либо . Для обоих случаев дисперсия результата складывается из отдельных дисперсий: и

Такое же соотношение справедливо не только для дисперсии, но и вероятной ошибки Ф и т.д.

Рассмотрим ошибку, возникающую при определении числа Рейнолдса:

Число Рейнолдса =

Допустим, в результате измерений в потоке горючего в топливо­проводе для двух режимов расхода топлива была заполнена таблица:

Величина	Мин. расход	Макс. Расход	Ошибка Ф, %
			Мин. расход	Макс. расход
Скорость V, м/сек	0.5	10.0	12	2
Диаметр трубы D, см	2.0	2.0	0.000	0.000
Плотность горючего ,	0.6	0.6	0.1	0.1
Вязкость горючего ,	0.001	0.001	0.5	0.5

В режиме минимального расхода топлива вероятная ошибка в опре­делении числа Рейнолдса оказывается равной:

В режиме максимального расхода вероятная ошибка равна:

Таким образом, с ростом расхода топлива и, соответственно, чис­ла Рейнолдса величина интервала неопределённости в данном экспери­менте уменьшается. Математическая статистика оперирует с понятием доверительного интервала, в который с заранее заданным % вероятно­сти попадают результаты измерений. В данном случае доверительный ин­тервал может выглядеть таким образом:

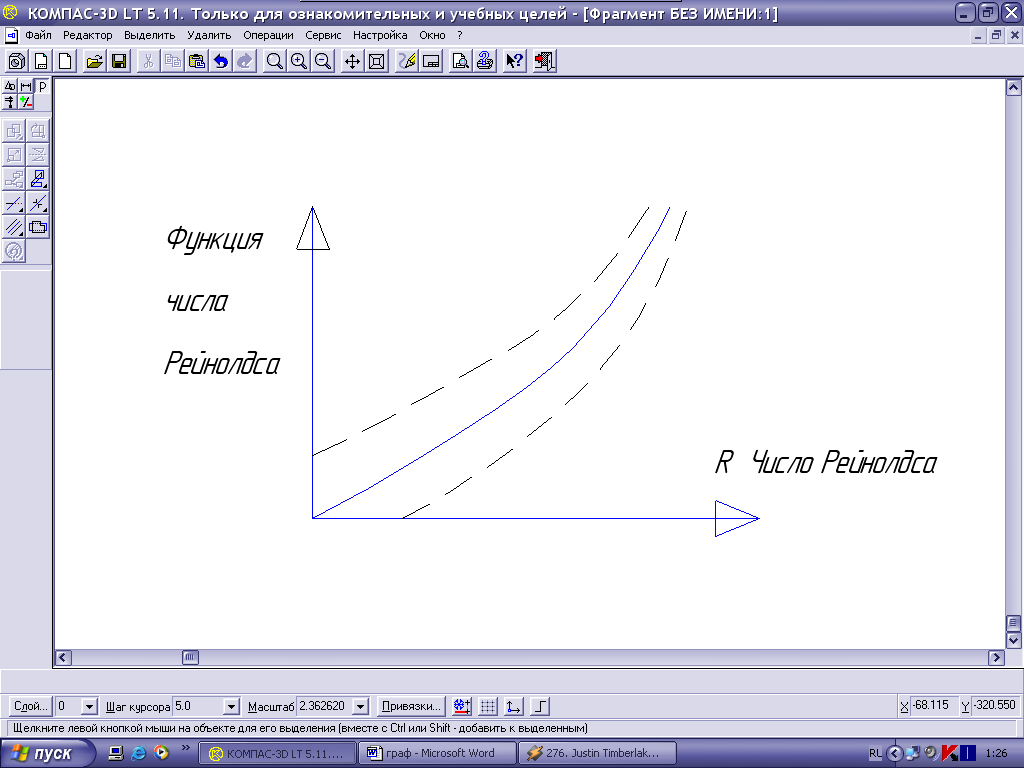
Рис. 9. 95% - ый- доверительный интервал при измерении числа Рейнолдса.

В случае, если результат измерений R представляет из себя не­которую функцию измеряемых величин то ин­тервал неопределённости результата рассчитывается как:

где - интервалы неопределённостей величин

Проанализировав каждый отдельный вклад в общую неопределённость инженер, убрав из рассмотрения малозначащие члены, может избежать из­лишних затрат на приобретение несущественного для повышения точнос­ти измерений оборудования.

В инженерной практике не всегда возможно иметь аналитическую зависимость результата измерений . В таком случае мож­но использовать табличные значения, Допустим, с помощью парового ка­лориметра зарегистрированы давление и темпера­тура пара Т = 130 1°С. Требуется выяснить максимальную неопреде­лённость в определении теплосодержания пара H(Р, Т) при этих усло­виях, если неизвестна аналитическая зависимость Н (P,T)

Располагая таблицей значений Н (кал/г) в интересующем иссле­дователя диапазоне:

P	T
	120	130	140
1.0	649.2	654.3	660.1
1.2	648.7	653.9	659.6
1.4	648.3	653.5	659.1

можно вместо точных значений производных и использо­вать приближённо значения конечных разностей:

Значит, если довериться табличным данным, то неопределённость теплосодержания пара составит примерно 0,5 кал/г.