1.3 Оценка случайной ошибки измерительной системы.

В инженерной практике обычно неизвестны ни вид распределения, ни его показатели. Можно попытаться оценить точность измерений, ос­новываясь на собственном опыте, либо исходя из спецификации фирмы-изготовителя прибора. Часто этого оказывается недостаточно. Напри­мер, если на приборе указана ошибка %, то неясно, представляют ли эти % среднеквадратическое отклонение, или вероятную ошибку Ф.

Инженеру, приобретающему оборудование, желательно знать:

- какой процент отсчётов находится в пределах гарантированного фирмой интервала;

- распределены ли показания прибора по нормальному закону.

Существует простое правило оценки ошибки прибора: максимальная ошибка равна половине наименьшего деления на шкале. Например, для автомобильного манометра ошибка составляет 0,1/2 = 0,05 кг/ . Отклонение измеренного давления от истинной величины вряд ли превышает значение 0,05 кг/ .

Простым и доступным в производственных условиях способом про­верки нормальности распределения является нанесение значений откло­нений на вероятностную бумагу. Шкала на этой бумаге построена таким образом, что нормально распределённая совокупность ложится на пря­мую линию. Для этого по оси X откладываются отклонения от истинного значения измеряемой величины, а по оси Y через равные интервалы от­кладываются вычисленные для нормального распределения проценты от­счётов, имеющие отклонения, меньшие X. Рассмотрим пример построения графика на вероятностной бумаге.

Допустим, студентами произведено 30 измерений твёрдости по Бринелю, т.е. по диаметру вдавливаемого шарика, причём известно истин­ное значение твёрдости, Сведём все полученные значения диаметров в таблицу:

Отклонение диаметра от истинного, мм	-0,4	-0,3	-0,2	-0,1	0	0,1	0,2	0,3
Число отклонений	1	1	1	3	13	6	3	2
Число отсчетов, не превышающих данного	1	2	3	6	19	25	28	30
% отклонений, не превышающих данного	3,3	6,6	9,9	19,8	64,5	83,5	93,5	100

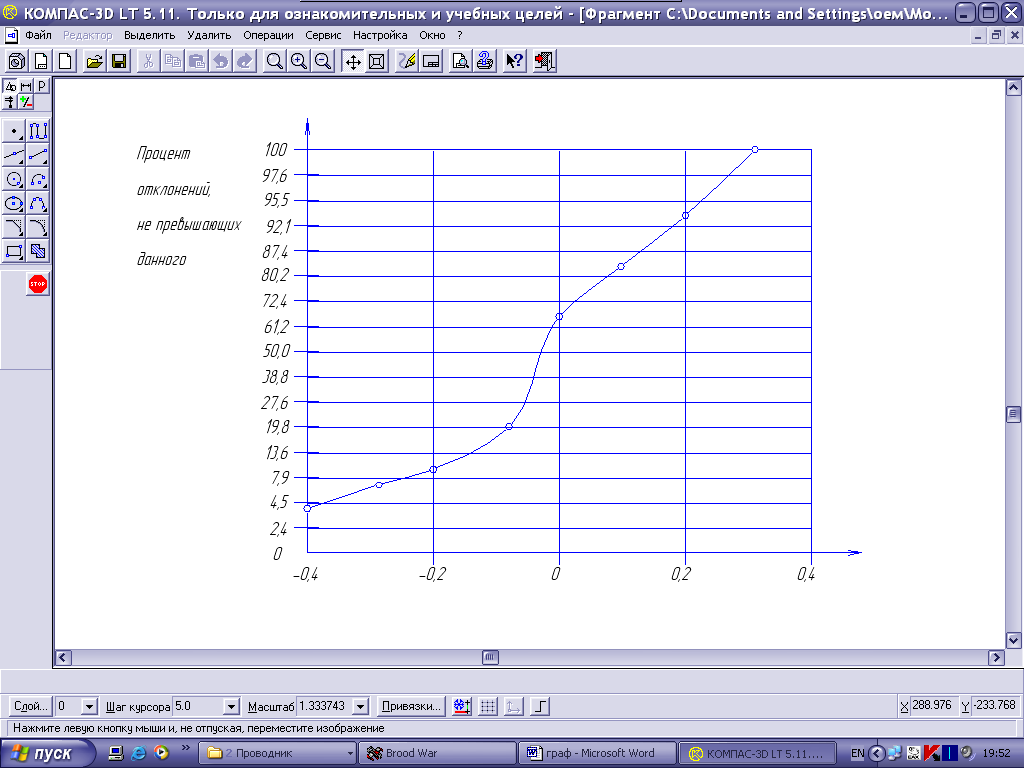Исходя из данных таблицы 2, построим график на вероятностной бумаге:

Даже невооружённым глазом видно, что измерения не ложатся на прямую, что не свидетельствует о близости выборки к части генераль­ной совокупности с нормальным распределением.

Д

По виду графиков, нанесённых на вероятностную бумагу, можно су­дить о характере распределения:

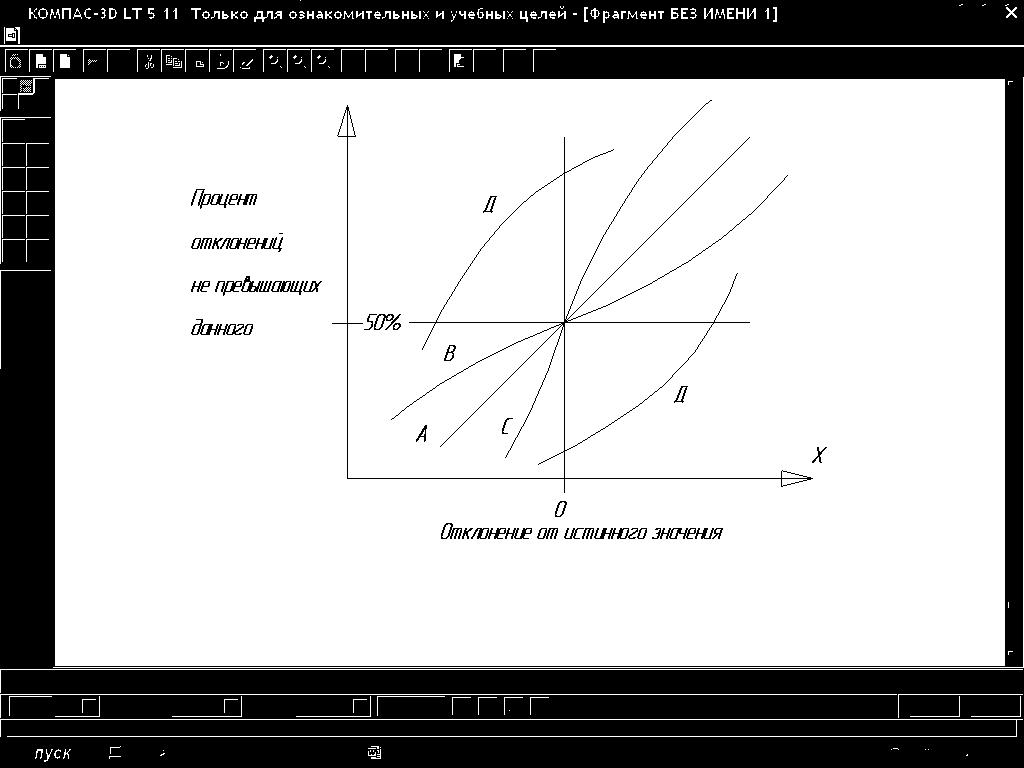
Рис. 6. А – нормальное распределение, симметричное относительно истинного значения;

В – симметричное, но расплывшееся распределение;

С – симметричное, но сжатое к истинному значению;

Д – ассиметричное распределение.

Если распределение существенно отличается от нормального, то это может свидетельствовать о неисправности прибора, либо о непра­вильном обращении с ним.