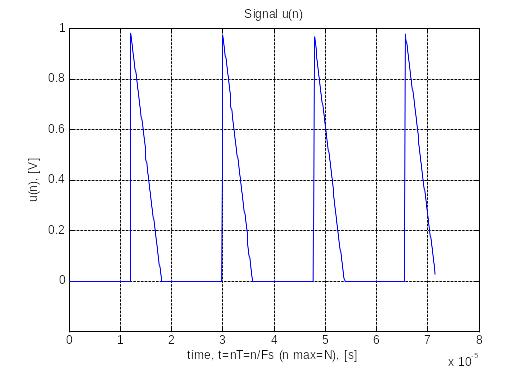
Наша последовательность:

В увеличенном виде:

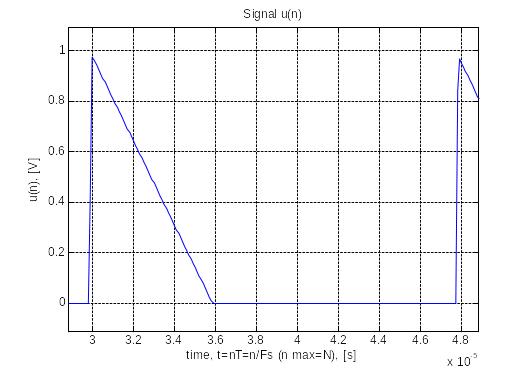
Видим, что передний фронт бесконечной крутизны, длительность импульса 6 мкс, длительность паузы между импульсами 12 мкс.

Спектры сигнала:

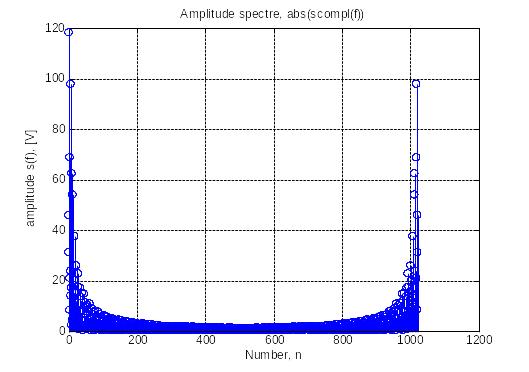
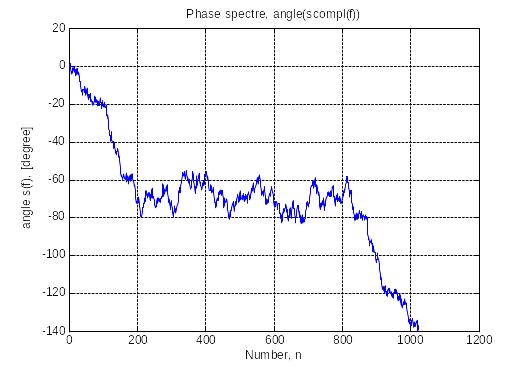
Таблица с характеристиками сигнала:

№ п/п	Наименование параметра	Значение параметра
		№ частотного отсчета	Частота, f		Круговая частота,
			Абсолютная	Нормированная	Абсолютная	Нормированная
	Частота компоненты спектра, имеющей максимальный уровень	0	0	0	0	0
	Ширина основного лепестка по уровню 0,5	11	107кГц	0,0107	671кГц	0,0672
	Ширина основного лепестка по ближайшим нулям (нулю)	20	195кГц	0,0195	1224кГц	0,12246
	Частота компоненты спектра, имеющей уровень, ближайший к максимальному	6	58кГц	0,0058	364кГц	0,0364
	Частота компоненты, имеющей следующий уровень	5	49кГц	0,0049	307кГц	0,0307
	Частота компоненты, имеющей следующий уровень	11	107кГц	0,0107	671кГц	0,0672
		Абсолютное, ед	Нормированное, ед		Нормированное, дБ
	Значение максимальной компоненты	118	1		0
	Значение компоненты, ближайшей по уровню к максимальной	98	0,83		-0,8
	Значение следующей компоненты спектра	68	0,58		-2,3
	Значение следующей компоненты спектра	62	0,52		-2,8

Задание 3.

Одиночный Гауссов радиоимпульс на несущей частоте =3 МГц, относительной шириной спектра 10% от несущей на уровне -10 дБ.

Код программы:

clear; % очищаем память

t0=0; % начало импульса 0 с.

Fs=48e6; % частота дискретизации 48 МГц

fc=3e6; % несущая частота в герцах

bw=0.1; %относительная ширина спектра (ширина спектра, деленная на несущую частоту)

bwr=-10; %уровень (в децибелах), по которому производится измерение ширины спектра).

taui=2e-6; % длительность импульса 2 мкс

t=t0-taui/4:1/Fs:t0+2*taui; % вектор дискретных значений времени t(n)

u=gauspuls(t, fc, bw, bwr);

axis tight; % масштаб такой, чтобы вошел весь диапазон значений по обеим осям

plot(t,u); % график сигнала

title('Signal u(n)'); % заголовок графика

xlabel('time, t=nT=n/Fs (n max=N), [s]'); % надписи по горизонтальной оси

ylabel('u(n), [V]'); % надписи по вертикальной оси

%ylim([-0.1 1.1]) %масштаб по оси ординат (минимальное и максимальное значение)

Nfft=2^nextpow2(length(u)); % ближайшая к числу отсчетов степень двойки

scompl=fft(u,Nfft); % комплексный спектр сигнала

s=abs(scompl); % амплитудный спектр сигнала

phi=180/pi*angle(scompl); % фазовый спектр сигнала

figure; % создание нового окна

f =0:Nfft-1; % вектор отсчетов нормированной частоты для построения ДПФ

f=(f/(Nfft-1))*Fs; % вектор отсчетов частоты для ДПФ

stem(f,s); % отображение амплитудного спектра

title('Spectre abs(scompl(f))');

xlabel('Number, n');

ylabel('amplitude s(f), [V]');

figure;

phi=unwrap(phi); % сглаживаем график фазового спектра

plot(phi); % построение фазового спектра

title('Spectre angle(scompl(f))');

xlabel('Number, n');

ylabel('angle s(f), [degree]');