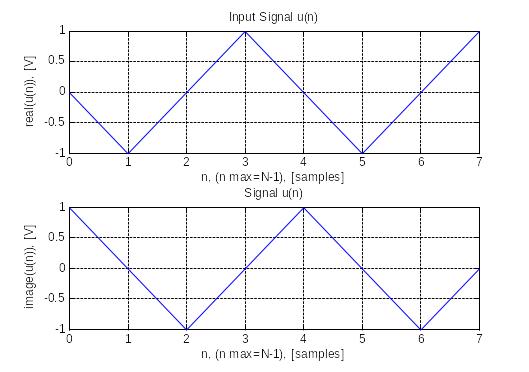
1. Выполните БПФ сигнала u(n) = j; -1; -j; 1; j; -1; -j; 1. Заполните таблицу с исходными данными, промежуточными и окончательными результатами вычислений.

%ИССЛЕДОВАНИЕ СВОЙСТВ БПФ ДЛЯ N=8

%ФОРМИРОВАНИЕ ВЕКТОРА ВХОДНОГО СИГНАЛА un (КОМПЛЕКСНЫЙ)

N=8

n=1:N; %вектор номеров отсчетов n

f=6/N

%un=cos(2*pi*f*n); % сигнал косинусоидальный

un=[j -1 -j 1 j -1 -j 1]; % сигнал экспоненциальный

% ПОСТРОЕНИЕ ГРАФИКА СИГНАЛА (ДЕЙСТВИТЕЛЬНОЙ И МНИМОЙ ЧАСТИ)

subplot(2,1,1)

axis tight; % масштаб такой, чтобы вошел весь

% диапазон значений по обеим осям

plot(n-1,real(un)); % график сигнала

title('Input Signal u(n)'); % заголовок графика

xlabel('n, (n max=N-1), [samples]'); % надписи по горизонтальной оси

ylabel('real(u(n)), [V]'); % надписи по вертикальной оси

grid on

subplot(2,1,2)

axis tight; % масштаб такой, чтобы вошел весь

% диапазон значений по обеим осям

plot(n-1,imag(un)); % график сигнала

title('Signal u(n)'); % заголовок графика

xlabel('n, (n max=N-1), [samples]'); % надписи по горизонтальной оси

ylabel('image(u(n)), [V]'); % надписи по вертикальной оси

grid on

% ВЫЧИСЛЕНИЕ 4-Х ДВУХТОЧЕЧНЫХ БПФ

s21=[un(1)+un(5) un(1)-un(5)] %вектор первого (из четырех) двухточечного БПФ

s22=[un(3)+un(7) un(3)-un(7)] %вектор второго (из четырех) двухточечного БПФ

s23=[un(2)+un(6) un(2)-un(6)] %вектор третьего (из четырех) двухточечного БПФ

s24=[un(4)+un(8) un(4)-un(8)] %вектор четвертого (из четырех) двухточечного БПФ

% ВЫЧИСЛЕНИЕ 2-Х ЧЕТЫРЕХТОЧЕЧНЫХ БПФ ПО 4-М ДВУХТОЧЕЧНЫМ

s41=[s21(1)+s22(1) s21(2)-j*s22(2) s21(1)-s22(1) s21(2)+j*s22(2)] %вектор первого (из двух) четырехточечного БПФ

s42=[s23(1)+s24(1) s23(2)-j*s23(2) s23(1)-s24(1) s23(2)+j*s23(2)] %вектор первого (из двух) четырехточечного БПФ

% ВЫЧИСЛЕНИЕ ВОСЬМИ ТОЧЕЧНОГО БПФ ПО ДВУМ ЧЕТЫРЕХТОЧЕЧНЫМ

s8=[s41(1)+s42(1) s41(2)+(exp(-j*pi/4))*s42(2) s41(3)+(exp(-j*pi/2))*s42(3) s41(4)+(exp(-j*3*pi/4))*s42(4) s41(1)-s42(1) s41(2)-(exp(-j*pi/4))*s42(2) s41(3)-(exp(-j*2*pi/4))*s42(3) s41(4)-(exp(-j*3*pi/4))*s42(4)] %вектор восьмиточечного БПФ

% ВЫЧИСЛЕНИЕ АМПЛИТУДНОГО И ФАЗОВОГО СПЕКТРОВ

scompl=s8; % результат выполнения восьмиточечного БПФ

s=abs(scompl); % амплитудный спектр сигнала

phi=(180/pi)*angle(scompl); % фазовый спектр сигнала

% ПОСТРОЕНИЕ ГРАФИКОВ АМПЛИТУДНОГО И ФАЗОВОГО СПЕКТРОВ

figure

k=n;

subplot(2,1,1) %определение места №1 графика в матрице 1х2

stem(k-1,s); % построение амплитудного спектра

title('SPECTR N=8') %заголовок

xlabel('k, (kmax=N-1), [frequency samples]') %подпись по оси x

ylabel('Magnitude, [V]') %подпись по оси y

grid on % добавление сетки

subplot(2,1,2) %определение места №2 графика в матрице 1х2

stem(k-1,phi) % построение ФЧХ

xlabel('k, (kmax=N-1), [frequency samples]') %подпись по оси x

ylabel('Phase, [degrees]') %подпись по оси y

grid on % добавление сетки

Параметры
	1	2	3	4	5	6	7	8
	j	-1	-j	1	j	-1	-j	1
1-я итерация
	0 + 2.0000i	0	0	0	-2	0	2	0
2-я итерация
	0	0	0 + 4.0000i	0	0	0	-4	0
3-я итерация
	0	0	-0.0000 + 8.0000i	0	0	0	0	0

2. Выполните прямое ДПФ с помощью программы fft с размером выборки 64 для косинусоидального сигнала для случая, когда на выборке укладывается целое количество периодов входного сигнала 16 и для нецелого количества периодов 16,5, 19.

Для уменьшения эффекта растекания спектра примените к весовую функцию – окно Блэкмена.

По результатам вычислений заполните таблицу.

Таблица – Спектр гармонического сигнала (основная область) для различных значений периода

Функция
№ част. отсчета	0	1	2	3	4	5	6	7	8	9	10
Значение	0	0	0	0	32	0	0	0	0	0	0
Функция
№ част. отсчета	0	1	2	3	4	5	6	7	8	9	10
Значение	1.92	2.06	2.63	4.83	30.77	2.97	1.42	0.88	0.62	0.46	0.37
Функция
№ част. отсчета	0	1	2	3	4	5	6	7	8	9	10
Значение	1.36	2.29	5.34	24.02	15.925	6.75	4.48	3.43	2.82	2.41	2.12
Функция , взвешивание по Блэкмену
№ част. отсчета	0	1	2	3	4	5	6	7	8	9	10
Значение	0.01	0.01	0.01	0.01	2.16	9.48	13.01	6.49	0.80	0.001	0.001

1. Выполним прямое ДПФ для косинусоидального сигнала с периодом =16 (рис. 8,а) – на периоде БПФ содержится целое количество периодов сигнала .

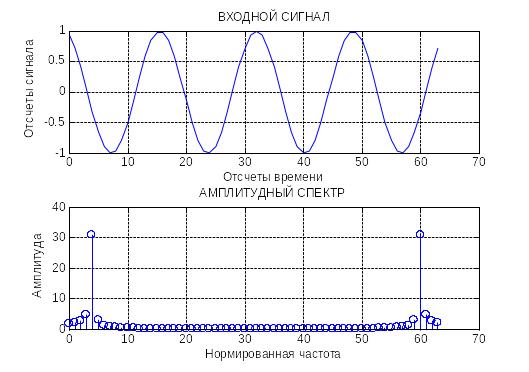
T=16

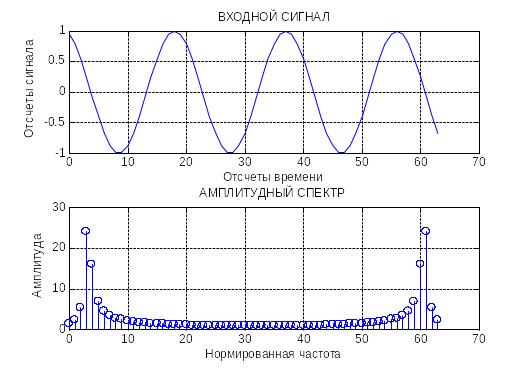
T=16.5

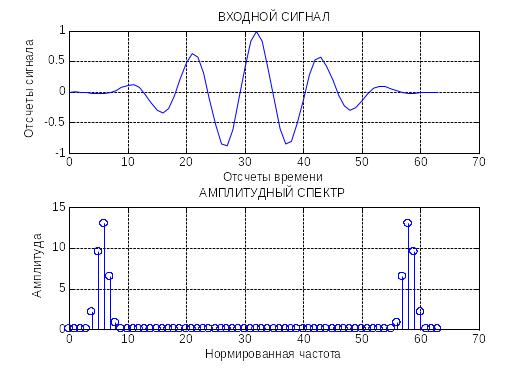
T=19

Взвешивание по блэкмэну T=11

3. Для когерентно-импульсной РЛС (см. рис.3) рассчитайте параметры гребенчатого фильтра на базе процессора ДПФ (минимально необходимый размер выборки и период (интервал) дискретизации ) для выработки оценок радиальной составляющей скорости целей. Значение несущей частоты РЛС 2 ГГц, максимальное значение радиальной скорости цели 4500 км/ч, потенциальное значение ошибки не должно превышать 15 м/с. Для упрощения задачи время прихода сигнала будем считать известным, шумовой и динамической ошибкой в оценках точности можно пренебречь.

Определите реакцию ДПФ-процессора на сигнал, отраженный от цели, имеющей радиальную составляющую скорости 125; 1250; 12,5; 0 м/с.

Решение

1. Синтез гребенчатого фильтра на основе процессора ДПФ проведем на основе схемы когерентно-импульсной РЛС (см. рис.3). Для определения параметров измерителя проанализируем исходные данные

Максимальное значение доплеровской частоты в соответствии с условиями задачи составит , где м/с - скорость распространения электромагнитной энергии в вакууме. Подставив заданные в условиях задачи значения несущей частоты РЛС 2 ГГц и максимальной радиальной скорости цели 4500 км/ч = 1250 м/с получаем 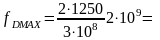16,66 кГц.

Для удовлетворительного воспроизведения формы сигнала (доплеровской огибающей) необходимо, чтобы на период изменения сигнала приходилось не менее 2-ух отсчетов (частота следования зондирующих импульсов РЛС была бы по крайней мере в два раза выше) 33,32 КГц..

Аналогично, разрешение по допплеровской частоте, необходимое для обеспечения необходимой точности выработки оценок радиальной скорости процессором БПФ, должно быть не хуже = 200 Гц.

Вычисление диапазона доплеровских частот и значения допплеровской частоты для 125 м/с производим следующим образом

%ДОППЛЕРОВСКИЙ ДЕТЕКТОР

f=1e9; %несущая частота

vrmax=1250; %максимальная радиальная скорость

vrmin=12.5; %минимальная радиальная скорость

%(точность (чувствительность) измерения радиальной скорости)

vr=125 %действующая радиальная скорость

fdmax=2*vrmax*f/3e8;%максимальный допплер

fdmin=2*vrmin*f/3e8;%минимальный допплер

%(предел чувствительности допплеровского измерителя)

fd=2*vr*f/3e8; %текущий допплер

Период дискретизации (период следования импульсов РЛС) определим исходя из теоремы Котельникова – при максимальной допплеровской частоте на периоде изменения комплексной огибающей сигнала должно быть не менее 2-х отсчетов 30 мкс. Вычисление производится следующим образом

Fsl=fdmax*2; %период следования (период дискретизации), исходя из

%условия однозначного измерения максимального допплера

Создаем вектор сигнала при условии, что частота (период) дискретизации определяется максимальной доплеровской частотой, а размер выборки требованиями по разрешающей способности – в нашем случае минимальной доплеровской частотой

t=0:1/Fsl:1/fdmin; %вектор времени

n=t*Fsl; %отсчеты времени

un=exp (j*2*pi*fd*t); %отсчеты сигнал

Таким образом, временная выборка для процессора ДПФ имеет интервал дискретизации, равный периоду следования импульсов, который, выбирается из условия однозначного измерения максимальной доплеровской частоты 30 мкс, размер выборки определяется минимальной допплеровской частотой 166

Вычисляем ДПФ от сигнала , поступившего с выхода АЦП строим графики сигнала и амплитудный спектр сигнала для радиальной скорости 125 м/с. Вариант программы вычисления БПФ может иметь следующий вид

1250

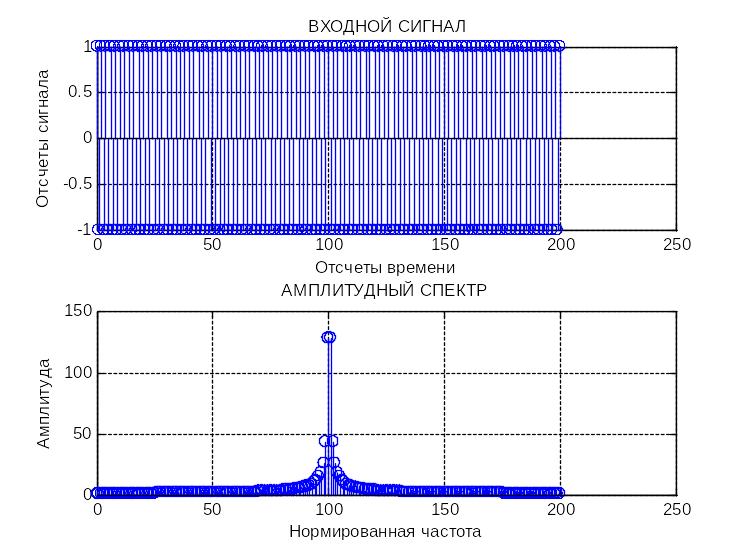
12,5

0

3. Оценить параметры ДПФ-процессора (минимально необходимый размер выборки и период (интервал) дискретизации ) для выработки оценок радиальной составляющей скорости целей при неизвестной дальности (неизвестном времени прихода сигнала). Исходные данные для расчета из примера 1, скважность последовательности зондирующих импульсов в РЛС КНИ 5.

Задачу решить в общем виде – время прихода сигнала неизвестно. Шумовой и динамической ошибкой в оценках точности можно пренебречь.

Определите реакцию ДПФ-процессора на сигнал, отраженный от цели, имеющей значения радиальной составляющей скорости те же, что и в предыдущей задаче..

1. Синтез гребенчатого фильтра на основе процессора ДПФ проведем на основе схемы когерентно-импульсной РЛС. Для определения параметров измерителя проанализируем исходные данные

Максимальное значение доплеровской частоты в соответствии с условиями задачи составит , где м/с - скорость распространения электромагнитной энергии в вакууме. Подставив заданные в условиях задачи значения несущей частоты РЛС 17 ГГц и максимальной радиальной скорости цели 900 км/ч = 250 м/с получаем 16,66 кГц .

Для удовлетворительного воспроизведения формы сигнала (доплеровской огибающей) необходимо, чтобы на период изменения сигнала приходилось не менее 2-ух отсчетов (частота следования зондирующих импульсов РЛС была бы по крайней мере в два раза выше) 33,32 КГц... Длительность зондирующих импульсов определяем исходя из скважности, заданной в исходных данных 4 мкс.

В связи с тем, что время прихода отраженного сигнала неизвестно мы должны принять период дискретизации таким, чтобы, как минимум, исключить пропуск импульса и, как максимум, обеспечить возможно более полное отображение (воспроизведение) формы импульса при выполнении аналогово-цифрового преобразования. Исходя из приведенных здесь соображений, выбираем период дискретизации так, чтобы на длительности импульса было не менее двух отсчетов .

Размер выборки для процессора ДПФ определяется путем деления периода минимальной доплеровской частоты на период дискретизации .

fdmax = 1.6667e+004

fdmin = 166.6667

vr = 125

Fsl = 8.3333e+003

taui = 2.4000e-005

T = 1.2000e-005

N = 500.0000

2. Создаем вектор сигнала при условии, что сигнал представляет собой две квадратурные последовательности видеоимпульсов треугольной формы, длительностью частотой следования , промодулированные допплером цели. Программа вычислений может выглядеть следующим образом

t=0:T:1/fdmin;%вектор времени

n=t/T; %временные отсчеты

d=(0:(Fsl/fdmin))' *1/Fsl;%вектор описывающий положение импульсов сигнала

%на временной оси

%в пределах n от 0 до N

un1=pulstran(t,d,'tripuls',2*taui); %последовательность треугольных

%после оптимальной фильтрации в приемнике) видеоимпульсов

un=un1.*exp(j*2*pi*fd*t); %отсчеты сигнала, полученные в результате

%выделения с помощью ФД модуляции последовательности видеоимпульсов

%допплером цели

3. Вычисляем ДПФ от сигнала , поступившего с выхода АЦП , строим графики сигнала и амплитудный спектр сигнала для радиальной скорости 125 м/с. Вариант программы вычисления БПФ может иметь следующий вид

scompl=fft(un);% комплексный спектр сигнала

s=abs(scompl); % амплитудный спектр сигнала

phi=180/pi*angle(scompl); % фазовый спектр сигнала

subplot(2,1,2) %определение места №2 графика в матрице 1х2

stem(n, s); % построение амплитудного спектра

title('АМПЛИТУДНЫЙ СПЕКТР') %заголовок

Xlabel('Нормированная частота') %подпись по оси X

ylabel('Амплитуда') %подпись по оси y

grid on % добавление сетки

subplot(2,1,1) %определение места №1 графика в матрице 1х2

stem(n,un) %построение сигнала

title(' ВХОДНОЙ СИГНАЛ') %заголовок

Xlabel('Отсчеты времени') %подпись по оси X

ylabel('Отсчеты сигнала') %подпись по оси y

grid on % добавление сетки

Максимальный уровень сигнала наблюдаем на выходе n= 0 , что соответствует радиальной скорости V=125 м/с.

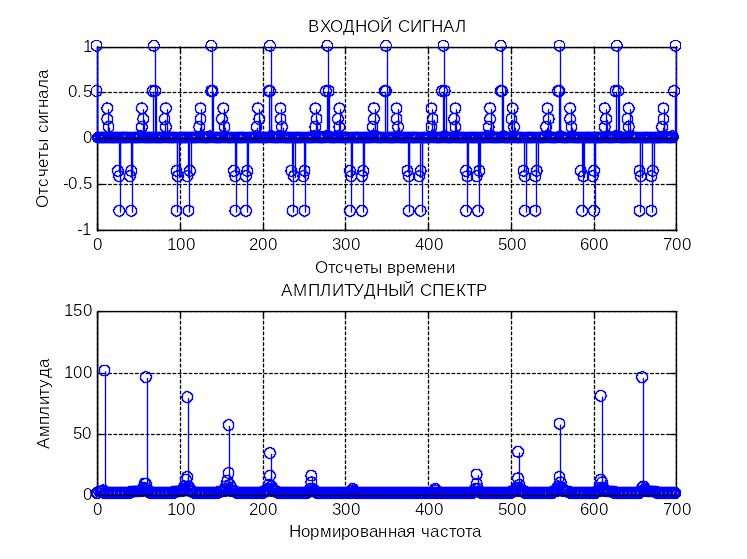
4. Выполним ДПФ сигнала , построим графики сигнала и амплитудный спектр сигнала при максимальной по условиям задачи радиальной скорости 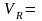1250 м/с. Максимальный уровень сигнала наблюдаем на выходе n=100, что соответствует радиальной скорости 1250 м/с.

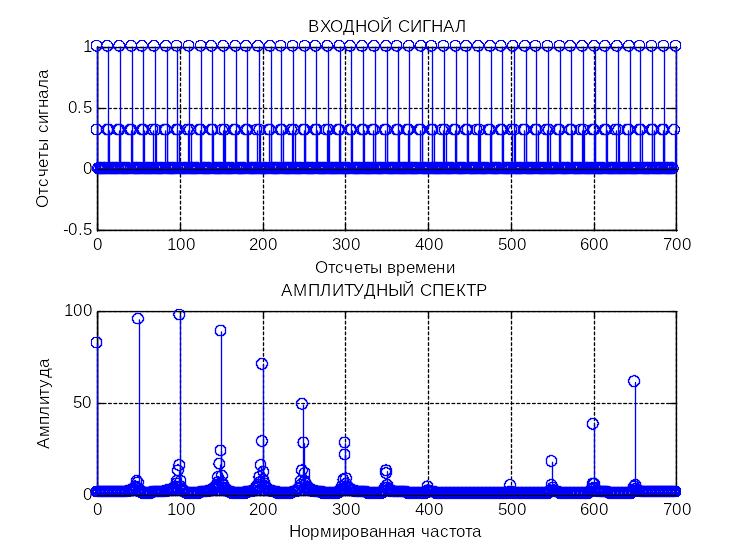
5. Выполним ДПФ сигнала , построим графики сигнала и амплитудный спектр сигнала при радиальной скорости, соответствующей разрешающей способности (чувствительности) 12,5 м/с.

Максимальный уровень сигнала наблюдаем на выходе n=0, что соответствует радиальной скорости 12,5 м/с.

6. Выполним ДПФ сигнала , построим графики сигнала и амплитудный спектр сигнала при отсутствии радиальной скорости цели .

Максимальный уровень сигнала наблюдаем на выходе n=0, что соответствует радиальной скорости V=0 м/с.

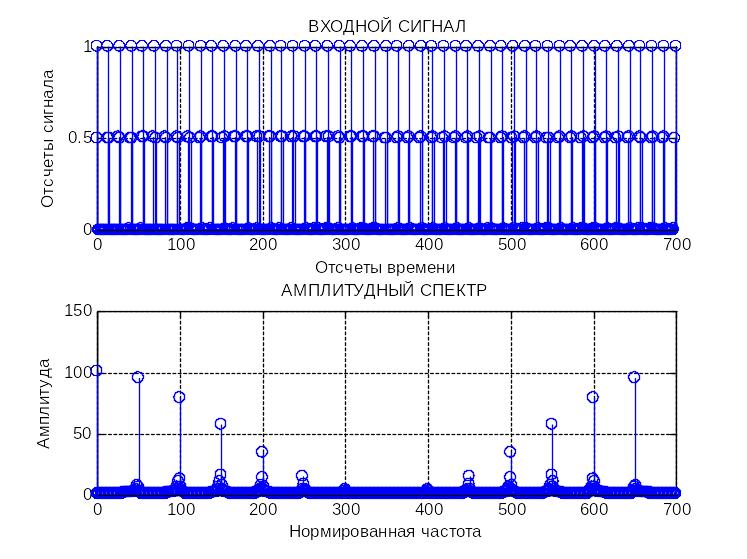
%ДОППЛЕРОВСКИЙ ДЕТЕКТОР (ВАРИАНТ ДЛЯ НЕИЗВЕСТНОГО ВРЕМЕНИ ПРИХОДА

%СИГНАЛА)

f=2e9; %несущая частота

vrmax=1250; %максимальная радиальная скорость

vrmin=12.5; %минимальная радиальная скорость

%(точность (чувствительность) измерения радиальной скорости)

fdmax=2*vrmax*f/3e8;%максимальный допплер

fdmin=2*vrmin*f/3e8;%минимальный допплер

%(предел чувствительности допплеровского измерителя)

vr=0 %текущая радиальная скорость

fd=2*vr*f/3e8; %текущий допплер

Fsl=fdmax/2 %период следования (ЗДЕСЬ НЕ РАВЕН периоду дискретизации), определяется исходя из

%условия однозначного измерения максимального допплера

taui=1/(Fsl*7)

T=taui/2 %интервал дискретизации

N=1/(fdmin*T)%размер выборки процессора ДПФ

t=0:T:1/fdmin;

n=t/T;

d=(0:(Fsl/fdmin))' *1/Fsl;

un1=pulstran(t,d,'tripuls',2*taui);

un=un1.*exp(j*2*pi*fd*t); %отсчеты сигнал

scompl=fft(un);% комплексный спектр сигнала

s=abs(scompl); % амплитудный спектр сигнала

phi=180/pi*angle(scompl); % фазовый спектр сигнала

subplot(2,1,2) %определение места №2 графика в матрице 1х2

stem(n, s); % построение амплитудного спектра

title('АМПЛИТУДНЫЙ СПЕКТР') %заголовок

xlabel('Нормированная частота') %подпись по оси x

ylabel('Амплитуда') %подпись по оси y

grid on % добавление сетки

subplot(2,1,1) %определение места №1 графика в матрице 1х2

stem(n,un) %построение сигнала

title(' ВХОДНОЙ СИГНАЛ') %заголовок

xlabel('Отсчеты времени') %подпись по оси x

ylabel('Отсчеты сигнала') %подпись по оси y

grid on % добавление сетки

3. Рассчитайте параметры фильтра на базе процессора БПФ, согласованного с одиночным ЛЧМ-импульсом, имеющим следующие параметры – длительность импульса , где - период дискретизации, - минимальное значение несущей частоты, - максимальное значение несущей частоты. Сравните полученные результаты фильтрации с аналогичным по длительности одиночным радиоимпульсом по крутизне нарастания выходного напряжения вблизи максимума.

Решение.

1. Синтез согласованного фильтра на основе процессора БПФ начнем с создания сигнала 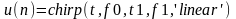, где - вектор значений времени, задают опорные точки для расчетов – в нулевой момент времени мгновенная частота равна , а в момент времени. она равна , закон изменения частоты линейный. Длину выборки примем равной 512 отсчетам ( ) Программа формирования ЛЧМ-сигнала может выглядеть следующим образом:

%БЫСТРАЯ СВЕРТКА. СОГЛАСОВАННЫЙ ФИЛЬТР НА БАЗЕ ПРОЦЕССОРА БПФ

%CИГНАЛ ЛЧМ

N=512 %размер выборки ДПФ

n=0:1:N; %вектор отсчетов времени

T=1 %период дискретизации

t=0:T:N*T; %вектор времени

f0=0.03 %минимальное значение частоты ЛЧМ-сигнала

f1=0.6 %максимальное значение частоты ЛЧМ-сигнала

t1=N*T %длительность ЛЧМ-сигнала (время изменения частоты от

%минимального до максимального значения

uin=chirp(t,f0,t1,f1,'linear'); %вычисление вектора отсчетов

%входного ЛЧМ-сигнала

2. Импульсная характеристика согласованного с сигналом фильтра должна являться зеркальным отражением сигнала. Сформируем импульсную характеристику фильтра в соответствии с этим определением

h=uin(N-n+1); %формирование вектора импульсной характеристики

%фильтра, согласованного с сигналом uin

3. Вид сигнала на выходе согласованного фильтра определится в результате выполнения операции быстрой свертки (выполнение БПФ ЛЧМ-сигнала, умножения на желаемую частотную характеристику и обратное БПФ) с помощью функции , порядок применения которой рассмотрен нами выше. Фрагмент программы приводится ниже и включает в себя кроме быстрой свертки также построение временной зависимости входного сигнала , импульсной характеристики фильтра , требуемой для осуществления согласованной фильтрации, и выходной последовательности отсчетов

uou=fftfilt(h,uin); %вычисление быстрой свертки

subplot(3,1,2) %определение места №2 графика в матрице 1х2

stem(h); % построение импульсной характеристики

title('ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА') %заголовок