Способ абсолютных разниц

Способ абсолютных разниц является одной из модификаций элиминирования. Как и способ цепной подстановки, он применяется для расчета влияния факторов на прирост результативного показателя в детерминированном анализе, но только в мультипликативных и мультипликативно-аддитивных моделях: Y=(a-b)c и Y=a(b-c). И хотя его использование ограничено, но благодаря своей простоте он получил широкое применение в АХД. Особенно эффективно применяется этот способ в том случае, если исходные данные уже содержат абсолютные отклонения по факторным показателям.

Регрессионный анализ и прогнозирование

Модели линейной регрессии (linear regression models) применяются в самых разных деловых ситуациях для установления зависимости между переменными, которые, как подсказывает аналитику его интуиция, должны быть между собой связаны. После того как зависимость установлена, ее можно использовать для прогнозирования. Обычно анализ методом регрессии используется для соотнесения продаж с ценой, мероприятиями по продвижению товара и рыночными факторами; курса акций с доходами и процентными ставками; затрат на производство с объемами выпуска. Но, конечно, его можно использовать также и для ответов на такие, например, вопросы: «Как влияет температура воздуха на продажу мороженого в стаканчиках?» Независимой переменной (independent variable) (X) в данном сценарии является температура. Это та переменная, от которой, как считается, зависит все происходящее. Зависимой переменной (dependent variable) (Y) будет объем продаж. Температура на улице влияет на объем продаж, но не наоборот.

Для анализа методом регрессии необходимо собрать данные, чтобы установить зависимость между переменными. Когда частных значений много, как в случае информации по изменениям температуры и объема продаж, можно построить график, откладывая по оси X значения температуры, а по оси Y — значения объема продаж. Цель анализа — составление уравнения линии, которая наилучшим образом отображает зависимость. При анализе методом регрессии стараются так провести линию между нанесенными на график точками, чтобы «значение суммы квадратов отклонений точек от линии было наименьшим». При работе методом наименьших квадратов (least squares method) требуется бесконечно складывать, вычитать и умножать. Для облегчения расчетов нужны деловой калькулятор или программа построения электронных таблиц.

Краткое воспоминание из алгебры

В порядке подготовки к рассмотрению примера на применение метода регрессии вспомним основы алгебры. Вы, конечно, не забыли, что линия описывается следующей формулой:

Y = аХ + b, где Y — зависимая переменная (например, объем продаж);

а — коэффициент, характеризующий наклон линии (зависимость между переменными);

X — независимая переменная (например, дождь);

b — отрезок на оси «Y» (точка, в которой линия пересекает вертикальную ось).

Компьютерная программа построения электронных таблиц рассчитывает линейное уравнение (Y = mX + b), описывающее связь между независимой и зависимой переменными. Программа определяет, можно ли в качестве точного инструмента прогнозирования использовать линию, которая рассчитана как наилучшим образом отображающая зависимость.

Владелец сети из двадцати магазинов Ben & Jerry ' s по продаже мороженого заметил, что объемы продаж растут и снижаются с ростом и по­нижением температуры воздуха соответственно. Решив определить точную математическую зависимость между объемом продаж и сезонными температурами, он собрал данные по ежемесячным объемам продаж за предыдущие пять лет, а в Национальной метеорологической службе получил информацию по среднемесячной температуре в соответствующие месяцы. В результате получилась следующая таблица:

Месяц	Среднемесячная температура		Объем продаж, долл.
	0F	0C
Январь	33	1	200 000
Февраль	37	3	250 000
Март	72	22	400 000
Апрель	65	18	500 000
Май	78	26	900 000
Июнь	85	29	1100 000
Июль	88	31	1500 000
Август	91	33	1300 000
Сентябрь	82	28	800 000
Октябрь	73	23	600 000
Ноябрь	45	7	300 000
Декабрь	36	3	500 000

Используя функцию «Regression» («Регрессия») программы построения электронных таблиц, владелец получил следующие данные:

Статистические данные

R²                                                                                                    0,704

Среднеквадратическая погрешность оценки Y                          243 334

Коэффициент, характеризующий точку пересечения оси Y   -379 066

Коэффициент X                                                                           16431

Среднеквадратическая погрешность коэффициента X            3 367

t-статистика переменной X                                                         4,88

Что означают эти данные?

Как ни парадоксально, но приведенные выше данные определяют уравнение линии, которое описывает зависимость между температурой за окном и объемом продаж в магазинах Ben & Jerry's. Сначала дадим толкование данных, которые необходимы для составления линейного уравнения.

«Коэффициент, характеризующий точку пересечения оси Y» = b = -379 066

«Коэффициент X» = m = 16 431

Подставляя эти значения в стандартное линейное уравнение, приведенное выше, получаем: Y = 16 43IX - 379 066. Наносим точки на график и проводим линию регрессии, описанную этим уравнением. В результате имеем следующее (рис. 1).

На графике видно, что линия регрессии проходит посредине между точками. Введя значение температуры X в уравнение, можно определить прогнозируемый (predicted) объем продаж мороженого. В случае магазинов Ben & Jerry's при температуре 60° F (15° С) ожидаемый объем продаж в месяц должен составить 606 794 долл.

Y = (16 431 X 60° F) - 379 066 = 606 794 долл.

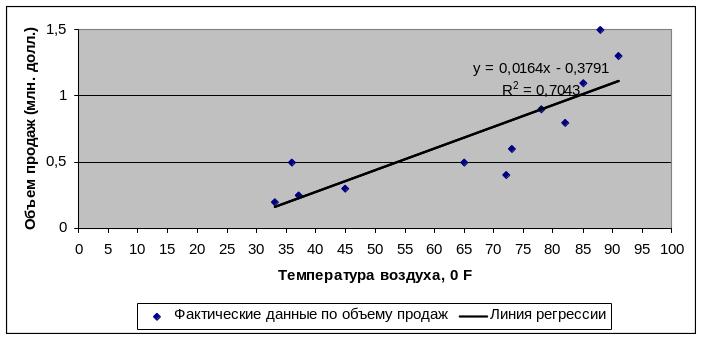
(График построен с помощью Мастера диаграмм в MS Excel)

Рис. 1. Пример анализа методом регрессии продаж мороженого фирмой Ben & Jerry ' s

Однако насколько точно данное уравнение позволяет прогнозировать продажи мороженого? Ответ на этот вопрос дает нам один из показателей, приведенных выше в статистических данных.

Пояснения по R

Значение R² показывает, «какой процент разброса данных объясняется конкретным уравнением регрессии». В нашем случае это 70,4% разброса данных по объему продаж. Такой показатель считается очень высоким. В широкомасштабном экономическом анализе очень высоким следует считать показатель 30%, так как на состояние экономики влияют тысячи переменных. Можно предположить, что в бизнесе, связанном с мороженым, на колебания объема продаж, помимо температуры, влияют также условия и длительность хранения продукта, реклама, предложение потребителям компенсационных купонов.

Однако не теряйте бдительности! Не пытайтесь вычитать слишком многое из результатов анализа методом регрессии! Они говорят нам только то, что объем продаж изменяется с температурой на улице во многом именно так, как описано. Из этого анализа не следует, что «именно температурой объясняется изменение объема продаж». Но если вы рационально и обоснованно выбрали независимую переменную и она хорошо предсказывает поведение исследуемой зависимой переменной, используйте анализ методом регрессии.

Анализ методом регрессии выявляет не только позитивную, как в случае с температурой воздуха и объемом продаж мороженого, но и негативную корреляцию, например, процентных ставок и объема продаж жилья. Если процентные ставки слишком высоки, объем продаж низок. В подобном случае коэффициент регрессии m имеет отрицательное значение. С точки зрения прогнозирования подобные негативные зависимости так же полезны, как позитивные.

Силбигер С. МВА за 10 дней / Пер. с англ. Э.В. Шустера. — 2-е изд. — М.: ЗАО «Консультант Плюс», 2002. — 440 с.

Пример 1. В таблице 1 определены показатели эффективности использования трудовых ресурсов. Рассчитаем влияние изменения среднесписочной численности работающих и средней выработки на прирост объема продукции (работ, услуг).

Таблица 1

Показатели	№ стр.	Базисный период (0)	Отчетный период (1)	Абсолютные отклонения	Индекс роста
1	2	3	4	5=4-3	6=4/3
Объем продукции (работ, услуг) в отпускных ценах, млн. руб. (V)	1	2400	2580	+180	1,075
Среднесписочная численность работающих, чел. (Т)	2	1800	1820	+20	1,0111
Средняя выработка одного работающего, тыс. млн. (В)	3	1,333	1,4176	+0,843	1,06319
Относительное высвобождение (-), дополнительное привлечение (+) работающих, чел.	4	X	X	1820-1800x1,075= =-115	X

Модель: V=Т*В

1. Способ цепных подстановок

а) влияние изменения численности работающих

ΔV_Т=Т₁В₀-V₀=1820*1,333-2400 = 2426,7-2400 = +26,7 (млн. руб.)

б) влияние изменения средней выработки работающего

ΔV_В=V₁-Т₁В₀=25800-2426,7 = + 153,3 (млн. руб.)

Общее изменение: ΔV_общ=V₁-V₀= ΔV_Т + ΔV_В = 2580-2400=26,7+153,3 = 180 (млн.р.)

Вывод: прирост продукции на 14,8 % (26,7/180*100) обеспечен за счет увеличения численности работающих и на 85,2 % (153,3/180*100) в результате роста производительности труда.

2. Способ абсолютных разниц

а) влияние изменения численности работающих

ΔV_Т =(Т₁-Т₀)*В₀ = ΔТ*В₀=(1820-1800)*1,333 = 20*1,333 = 26,7 (млн. руб.)

б) влияние изменения средней выработки работающего

ΔV_В=Т₁*(В₁-В₀) = Т_1*ΔВ=1820*(1,4176-1,3333) = 1820*0,0843 = 153,3 (млн. руб.)

3. Индексный метод

а) влияние изменения численности работающих

I_Т = = = 1,01111

б) влияние изменения средней выработки работающего

I_В = = = 1,06319

I_ГВ = = = 1,06319

Общее изменение: I_общ=I_Т*I_В=1,01111*1,06319 = 1,075

Вывод: См. лекции и учебники по статистике!

4. Способ относительных разниц

ΔТ%=(Т₁-Т₀)/Т₀*100; ΔВ%=(В₁-В₀)/ В₀*100

а) влияние изменения численности работающих

ΔV_Т=V₀* ΔТ%/100=2400*0,01111 = 26,7(млн. руб.)

б) влияние изменения средней выработки работающего

ΔV_В= (V₀+ ΔV_Т)* ΔВ%/100=(2400+26,7)*0,06319 = 153,3 (млн. руб.)

5. Интегральный способ.

а) влияние изменения численности работающих

ΔV_Т= ΔТ*В₀+ =26,7+ =26,7+0,8 = 27,5 (млн. руб.)

б) влияние изменения средней выработки работающего

ΔV_В= Т₀ *ΔВ+ = 151,7+ =151,7+0,8 = 152,5 (млн. руб.)

Общее изменение: ΔV_общ=V₁-V₀= ΔV_Т + ΔV_В=2580-2400=27,5+152,5=180 млн. р.

Вывод: прирост продукции на 15,3 % обеспечен за счет увеличения численности работающих и на 84,7 % в результате роста производительности труда.

6. Способ логарифмирования.

а) влияние изменения численности работающих

ΔV_Т = ΔV_общ * = 180* = 180* = 27,5 млн.р.

б) влияние изменения средней выработки работающего

ΔV_В= ΔV_общ * = 180* = 180* 0,84725 = 152,5 млн.р.

Общее изменение: ΔV_общ=V₁-V₀= ΔV_Т + ΔV_В=2580-2400=27,5+152,5=180 млн.р.

Вывод: прирост продукции на 15,3 % обеспечен за счет увеличения численности работающих и на 84,7 % в результате роста производительности труда.

Если среднегодовую численность работников в отчетном году сравнить с численностью работающих предыдущего года, скорректированную на коэффициент изменения объема продукции, то результат покажет относительную экономию численности работников: 115 чел. (1820-1800x1,075). Это означает, что для производства фактического количества продукции с сохранением планового показателя выработки потребовалось бы больше работающих на 115 чел. по сравнению с фактической численностью.

Проверка: + 1533,33 / 13,333 = 115

Задание 1. Определить показатели эффективности использования трудовых ресурсов, используя исходные данные таблицы 2. Произвести факторный анализ.

Таблица 2

Вариант	Объем продукции (работ, услуг) в отпускных ценах, млн. руб. (V)		Среднесписочная численность работающих, чел. (Т)
	План	Факт	План	Факт
1	5310	5018	4050	3975
2	6420	6851	6075	6111
3	4500	4663	4020	3998
4	3948	4048	3000	3015
5	8505	8388	5805	5852
6	6000	5850	5850	5819
7	5700	5511	5220	5267
8	7515	7848	6450	6390
9	6450	6053	5655	5640
10	9345	8967	7545	7800
11	7080	6691	5410	5290
12	8560	9135	8080	8169
13	6000	6218	5365	5311
14	5264	5264	4010	4040
15	9340	9184	7740	7802
16	8000	7890	7800	7758
17	7600	7348	6960	7022
18	10020	10464	8600	8520
19	8600	8070	7540	7520
20	12460	11957	9060	9398
21	3540	3345	2700	2650
22	4280	4567	4050	4074
23	3000	3109	2680	2666
24	2632	2632	2000	2010
25	5670	5592	3870	3901
26	4000	3900	3900	3879
27	3800	3674	3480	3511
28	5010	5232	4300	4260
29	4300	4035	3770	3760
30	6230	5978	5030	5199

Примечание: все расчеты производить с точностью до четвертого знака после запятой.

Пример 2. В таблице 3 рассчитаны показатели эффективности использования основных фондов. Определим влияние изменения среднегодовой стоимости основных фондов и коэффициента фондоотдачи на прирост объема продукции (работ, услуг).

Таблица 3

Показатели	№ стр.	Базисный период	Отчетный период	Отклонения
				абсолютное	%
1	2	3	4	5=4-3	6=5/3*100
Объем продукции (работ, услуг) в отпускных ценах, тыс. руб. (V)	1	24000	25800	+1800	+7,5
Среднегодовая стоимость ОПФ, тыс. руб. (F)	2	9340	9800	+460	+5,0
Коэффициент фондоотдачи KF	3	2,57	2,6327	+0,0631	+2,45
Коэффициент фондоемкости	4	0,39	0,38	-0,01	-2,56
Относительная экономия (-), перерасход (+) капитальных вложений, тыс. руб.	5	X	X	9800-9340x1,075= =-240,5	X

Модель: V=F*K^F

1. Способ цепных подстановок

а) влияние изменения среднегодовой стоимости ОПФ

ΔV_F=F₁K -F₀K =25182-24000=1182 (тыс. руб.)

б) влияние изменения коэффициента фондоотдачи

ΔV_K=F₁K -F₁K =25800-25182=618 (тыс. руб.)

2. Способ абсолютных разниц

а) влияние изменения среднегодовой стоимости ОПФ

ΔV_F=(F₁-F₀)*K =ΔF*K =(9800-9340)*2,57=460*2,57=1182 (тыс. руб.)

б) влияние изменения коэффициента фондоотдачи

ΔV_K=F₁*(K -K )= F_1*ΔK^F=9800*(2,633-2,57)=9800*0,063=618 (тыс. руб.)

Общее изменение: ΔV_общ=V₁-V₀= ΔV_Т + ΔV_В=25800-24000=1182+618=1800

Вывод: прирост продукции на 65,7 % (1182/1800*100) обеспечен за счет увеличения стоимости ОПФ и на 34,3 % (618/1800*100) в результате повышения фондоотдачи.

3. Индексный метод

а) влияние изменения среднегодовой стоимости ОПФ

I_F=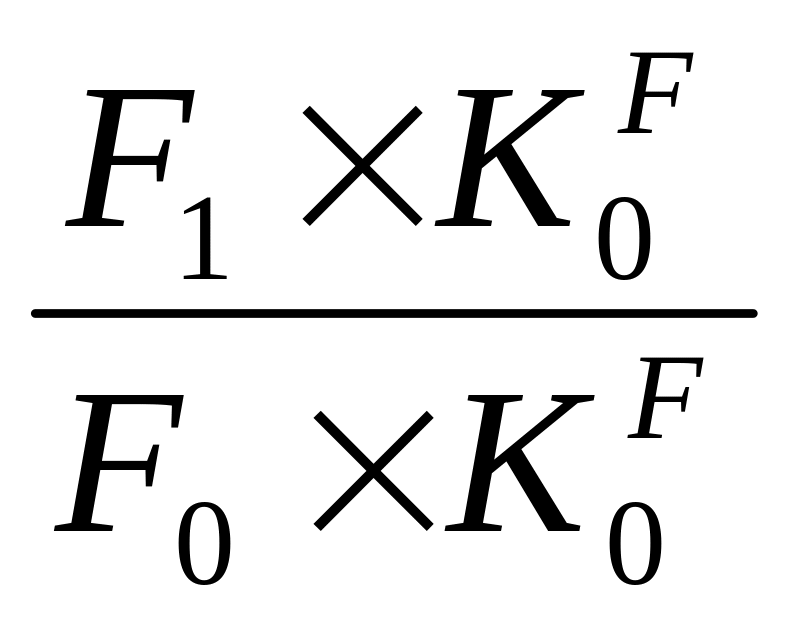 = =1,04925

б) влияние изменения коэффициента фондоотдачи

I_K=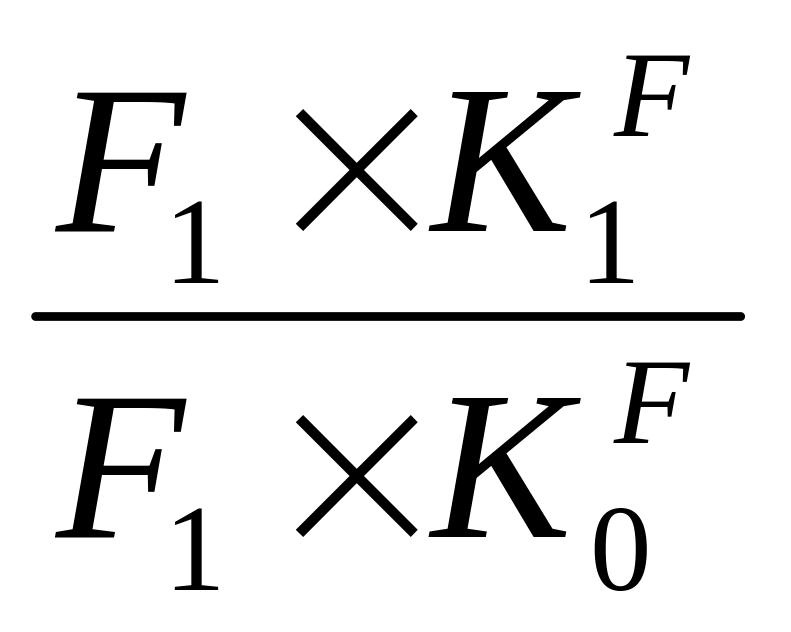 = =1,02454

Общее изменение: I_общ=I_F*I_K=1,04925*1,02454=1,075

Вывод:

4. Способ относительных разниц

ΔF%=(F₁-F₀)/F₀*100; ΔK^F%=(K -K )/ K *100

а) влияние изменения среднегодовой стоимости ОПФ

ΔV_F=V₀* ΔF%/100=1182 (тыс. руб.)

б) влияние изменения коэффициента фондоотдачи

ΔV_K= (V₀+ ΔV_F)* ΔK^F%/100=618 (тыс. руб.)

5. Интегральный способ.

а) влияние изменения среднегодовой стоимости ОПФ

ΔV_F= ΔF*K + =1182+ =1182+14,5=1196,5 (тыс. руб.)

б) влияние изменения коэффициента фондоотдачи

ΔV_K= F₀ ΔK^F+ =589 +14,5=603,5 (тыс. руб.)

Общее изменение: ΔV_общ=V₁-V₀= ΔV_F + ΔV_K=25800-24000=1196,5+603,5=1800 (т. р.)

Выводы по относительной экономии:

Задание 2. Определить показатели эффективности использования основных фондов, используя исходные данные таблицы 4. Произвести факторный анализ.

Таблица 4

Вариант	Объем продукции (работ, услуг) в отпускных ценах, млн. руб. (V)		Среднегодовая стоимость ОПФ, млн. руб. (F)
	План	Факт	План	Факт
1	5310	5018	2670	2835
2	6420	6851	3195	3006
3	4500	4663	2340	2407
4	3948	4048	1575	2022
5	8505	8388	4830	4634
6	6000	5850	2715	2918
7	5700	5511	2625	2547
8	7515	7848	3840	3805
9	6450	6053	3270	3304
10	9345	8967	6930	6868
11	7080	6691	3560	3780
12	8560	9135	4260	4009
13	6000	6218	3120	3210
14	5264	5264	2100	2696
15	9340	9184	6440	6179
16	8000	7890	3620	3891
17	7600	7348	3500	3396
18	10020	10464	5120	5074
19	8600	8070	4360	4406
20	12460	11957	9240	9157
21	3540	3345	1780	1890
22	4280	4567	2130	2004
23	3000	3109	1560	1605
24	2632	2632	1050	1348
25	5670	5592	3220	3089
26	4000	3900	1810	1945
27	3800	3674	1750	1698
28	5010	5232	2560	2537
29	4300	4035	2180	2203
30	6230	5978	4620	4578

Пример 3. В таблице 5 рассчитаны показатели эффективности использования материальных ресурсов. Определим влияние изменения стоимости материальных ресурсов и коэффициента материалоотдачи на прирост объема продукции (работ, услуг).

Таблица 5

Показатели	№ стр.	Базисный период	Отчетный период	Абсолютные отклонения	Индекс роста
1	2	3	4	5=4-3	6=4/3
Объем продукции (работ, услуг) в отпускных ценах, тыс. руб. (V)	1	24000	25800	+1800	1,075
Материальные затраты, тыс. руб. (М)	2	12100	16320	+4220	1,349
Коэффициент материалоотдачи KМ	3	1,983	1,581	-0,402	0,797
Коэффициент материалоемкости	4	0,50	0,63	+0,13	1,25
Относительная экономия (-), перерасход (+) материальных затрат, тыс. руб.	5	X	X	16320-12100*1,075= =+3312,5	X

Модель: V=М*K^М

1. Способ абсолютных разниц

а) влияние изменения стоимости материальных ресурсов

ΔV_М=ΔМ*K =4220*1,983=+8370 (тыс. руб.)

б) влияние изменения коэффициента материалоотдачи

ΔV_K= М_1*ΔK^М=16320*(-0,403)=-6570 (тыс. руб.)

Общее изменение: ΔV_общ=V₁-V₀= ΔV_М + ΔV_K=25800-24000=8370-6570=1800 (т. руб.)

2. Цепные подстановки и относительные разницы дают те же результаты.

3. Индексный способ (аналогично примерам 1 и 2).

4. Интегральный способ.

а) влияние изменения стоимости материальных ресурсов

ΔV_М= ΔМ*K + =8370+ =8370-849,5=7520,5 (тыс. руб.)

б) влияние изменения коэффициента материалоотдачи

ΔV_K= М₀ ΔK^М+ =-4871-849,5= -5720,5 (тыс. руб.)

Общее изменение: ΔV_общ=V₁-V₀= ΔV_М + ΔV_K=25800-24000=7520,5-5720,5=1800 (т. р.)

Относительный перерасход материальных затрат по данным таблицы составил 3312,5 тыс. руб. (16320-12100*1,015 или 16320-25800/1,983).

Это означает, что для производства фактического количества продукции с сохранением планового показателя материалоотдачи потребовалось бы меньше материальных ресурсов на 3312,5 тыс. руб. по сравнению с фактически израсходованными.

Задание 3. Определить показатели эффективности использования материальных ресурсов, используя исходные данные таблицы 6. Произвести факторный анализ.

Таблица 6

Вариант	Объем продукции (работ, услуг) в отпускных ценах, млн. руб. (V)		Материальные затраты, млн. руб. (М)
	План	Факт	План	Факт
1	5310	5018	2820	3285
2	6420	6851	3345	3141
3	4500	4663	2640	2725
4	3948	4048	1881	2173
5	8505	8388	5280	5084
6	6000	5850	2865	3218
7	5700	5511	3075	2847
8	7515	7848	4144	3954
9	6450	6053	3525	3633
10	9345	8967	7530	7348
11	7080	6691	3760	4381
12	8560	9135	4460	4189
13	6000	6218	3520	3634
14	5264	5264	2508	2898
15	9340	9184	7040	6778
16	8000	7890	3820	4291
17	7600	7348	4100	3796
18	10020	10464	5526	5272
19	8600	8070	4700	4844
20	12460	11957	10040	9753
21	3540	3345	1880	2190
22	4280	4567	2230	2094
23	3000	3109	1760	1817
24	2632	2632	1254	1449
25	5670	5592	3520	3389
26	4000	3900	1910	2145
27	3800	3674	2050	1898
28	5010	5232	2763	2636
29	4300	4035	2350	2422
30	6230	5978	5020	4876,5

Пример 4. Используя статистические функции «Корреляция» и «Линейная» проведем анализ корреляции между рядами динамики выпуска и реализации продукции и оплаты труда сотрудников по данным таблицы 7. Построим график.

Таблица 7

Динамика производства и реализации продукции в поквартальной разбивке, тыс. руб.

	Периоды
	2000 г.				2001 г.				2002 г
	I кв.	II кв.	III кв.	IV кв.	I кв.	II кв.	III кв.	IV кв.	I кв.
Товарная продукция (x1)	244,0	252,0	224,4	249,7	253,8	257,8	238,5	248,5	342,1
Реализованная продукция (x2)	193,5	260,4	262,6	312,2	237,8	277,1	228,4	291,4	263,1
ФОТ (Y)	141,9	192,7	222,2	218,8	182,2	206,8	197,4	212,5	209,3

Таблица 8