90. Критерий устойчивости (критерий Гурвица)

КРИТЕРИЙ УСТОЙЧИВОСТИ ГУРВИЦА.

Критерий устойчивости Гурвица относится к алгебраическим критериям устойчивости системы автоматического управления. Рассмотрим замкнутую систему автоматического управления структурная схема которой приведена к расчетной и имеет вид:

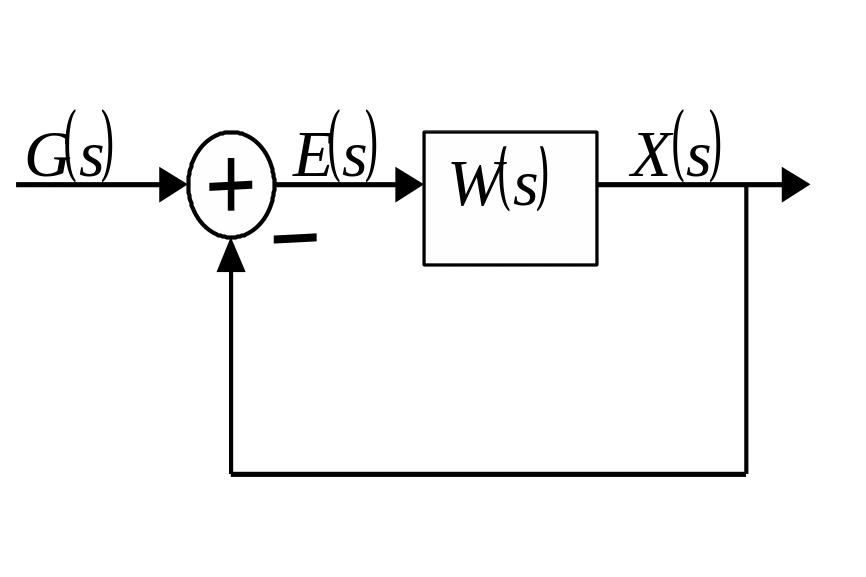
где - передаточная функция разомкнутой системы автоматического управления. Пусть далее , где и - полиномы относительно переменной степеней и соответственно, причем . Получим передаточную функцию замкнутой системы управления

.

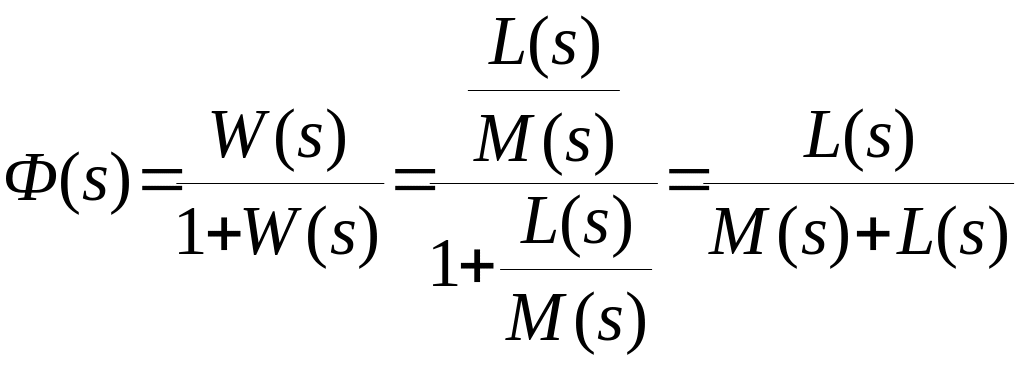Выпишем характеристический полином замкнутой системы:

;

.

Расположение корней характеристического полинома на плоскости определяет устойчивость замкнутой системы.

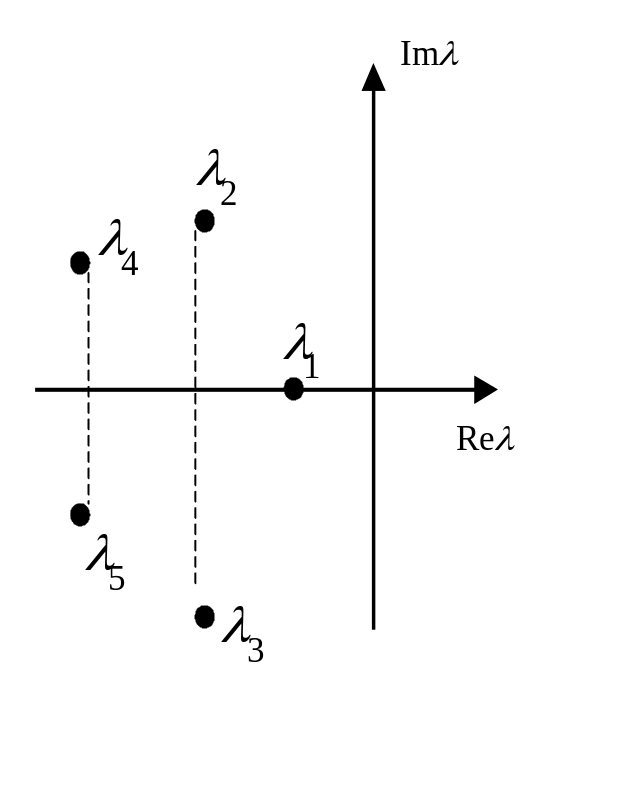
Критерий устойчивости Гурвица позволяет выполнить исследование устойчивости замкнутой системы управления, не решая характеристического уравнения

.

Составим квадратную матрицу размера из коэффициентов характеристического полинома замкнутой системы по следующему правилу:

1. По диагонали выписываем коэффициенты характеристического полинома, начиная с до в порядке возрастания индексов.

2. Каждая строка матрицы заполняется справа от диагонального элемента по убывающим индексам коэффициентов полинома.

3. Все элементы матрицы правее и левее заполняются нулями.

Иными словами столбцы вверх от главной диагонали дополняют коэффициентами характеристического полинома с последовательно возрастающими индексами. Столбцы ниже главной диагонали дополняют коэффициентами характеристического полинома с последовательно убывающими индексами. На место коэффициентов с индексами больше и меньше нуля – проставляют нули.

В результате чего получаем матрицу

.

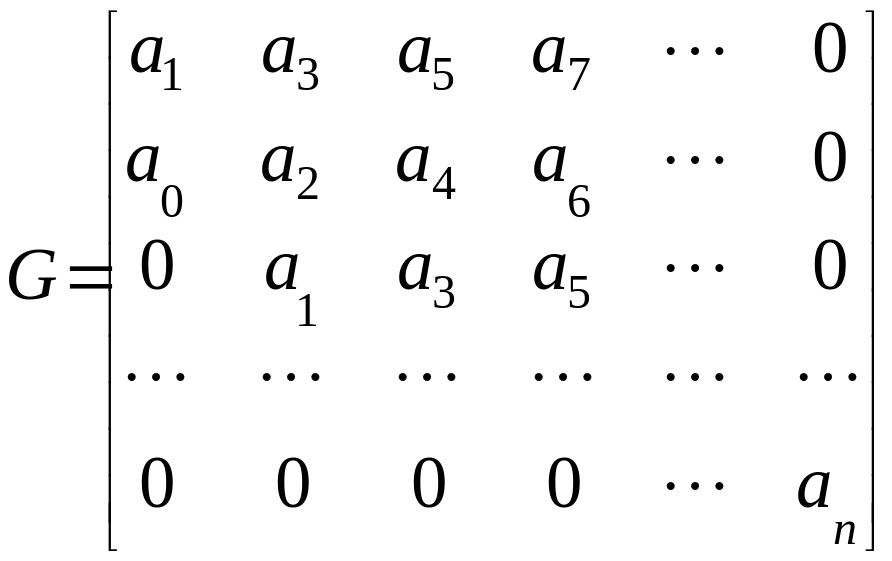Обозначим через , , … , - диагональные миноры матрицы .

Формулировка критерия устойчивости Гурвица.

Для того, чтобы замкнутая система автоматического управления была асимптотически устойчива необходимо и достаточно, чтобы все диагональные миноры матрицы были строго положительны, т.е. , , … , .

Для системы управления, характеристическое уравнение которых имеют низкую степень , условия устойчивости можно записать в общем виде.

Для имеем ,

, , , .

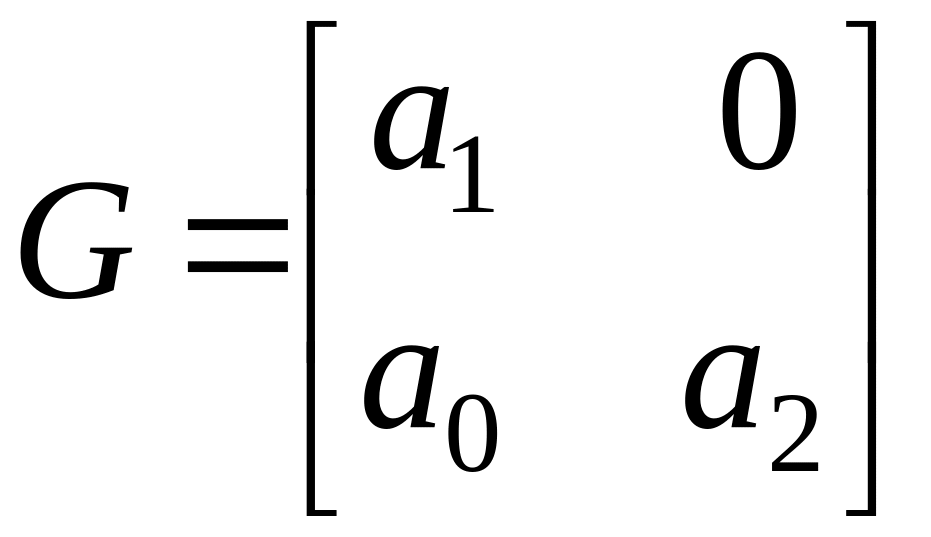, , необходимое условие устойчивости. Критерий устойчивости Гурвица определяет следующие условия устойчивости системы второго порядка , , . Следовательно, для систем второго порядка необходимые условия устойчивости являются и достаточными.

Для имеем .

,

, ,

, .

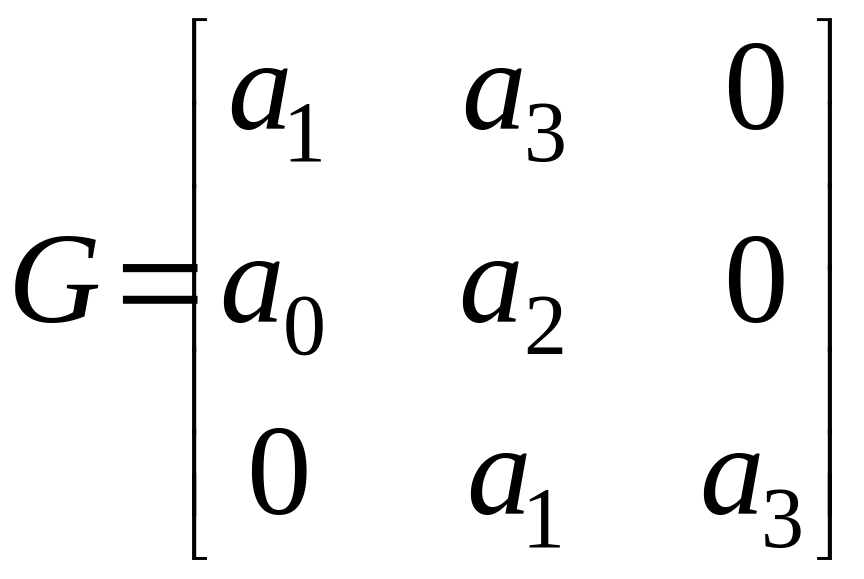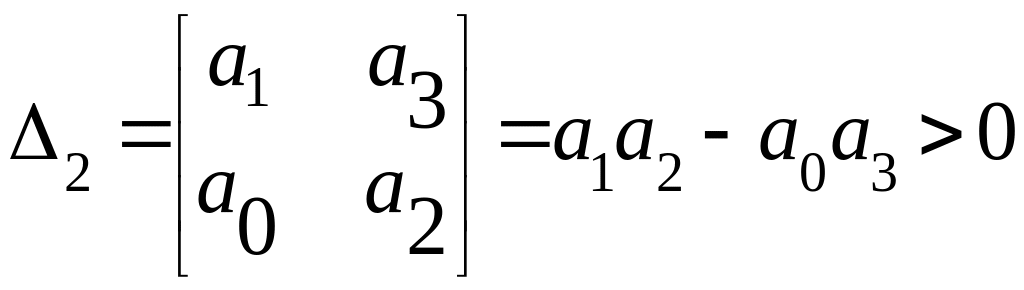Т.к. должно быть больше нуля, то .

Окончательно: , , .

Алгоритм исследования устойчивости систем автоматического управления с помощью алгебраического критерия Гурвица.

1. Преобразовать структурную схему системы автоматического управления к расчетной структурной схеме

где - передаточная функция разомкнутой системы.

2. По передаточной функции разомкнутой системы получить передаточную функцию замкнутой системы

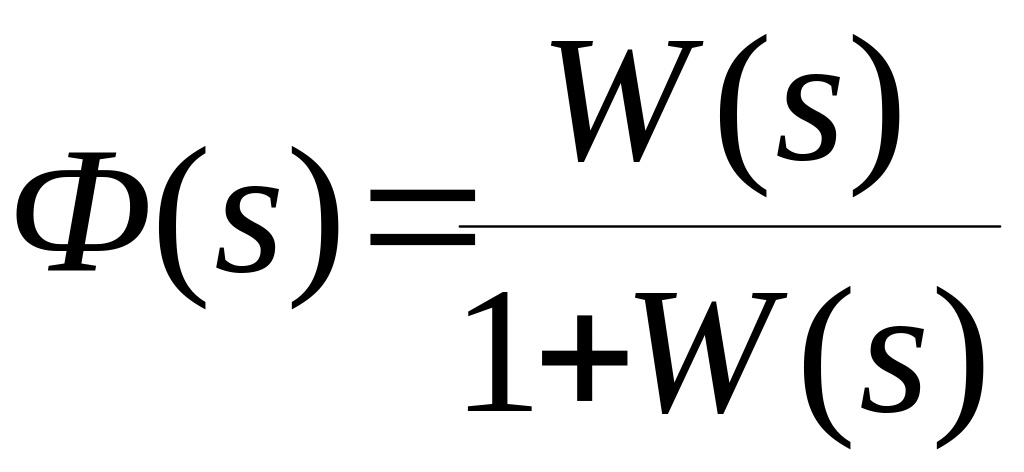
3. Выписать характеристический полином замкнутой системы .

4. Проверить необходимые условие устойчивости системы , , … ,

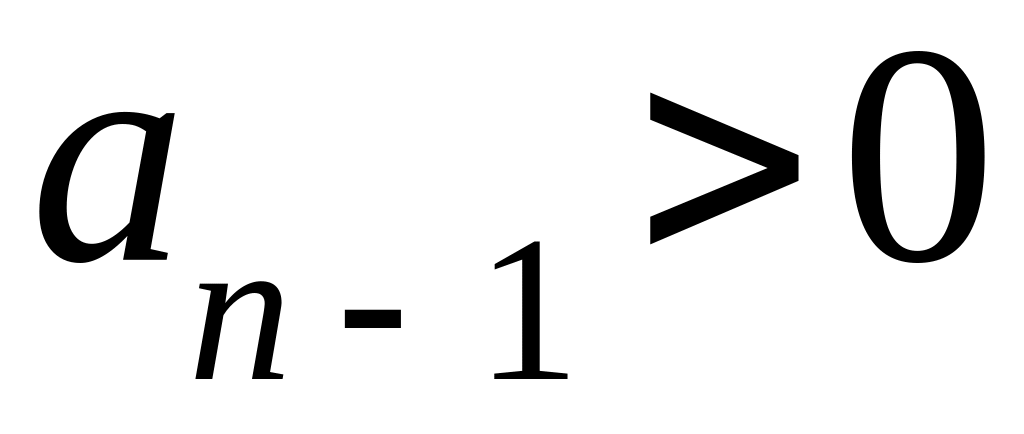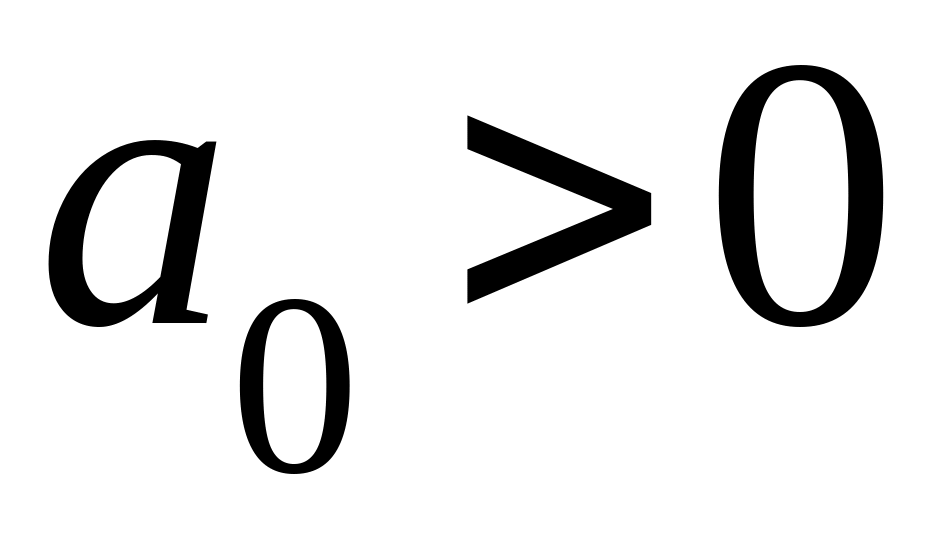
{если хотя бы одно из этих условий не выполнено, то система управления НЕУСТОЙЧИВА}

5. Составить матрицу Гурвица .

6. Последовательно вычисляя диагональные миноры матрицы , проверить их строгую положительность , , … ,

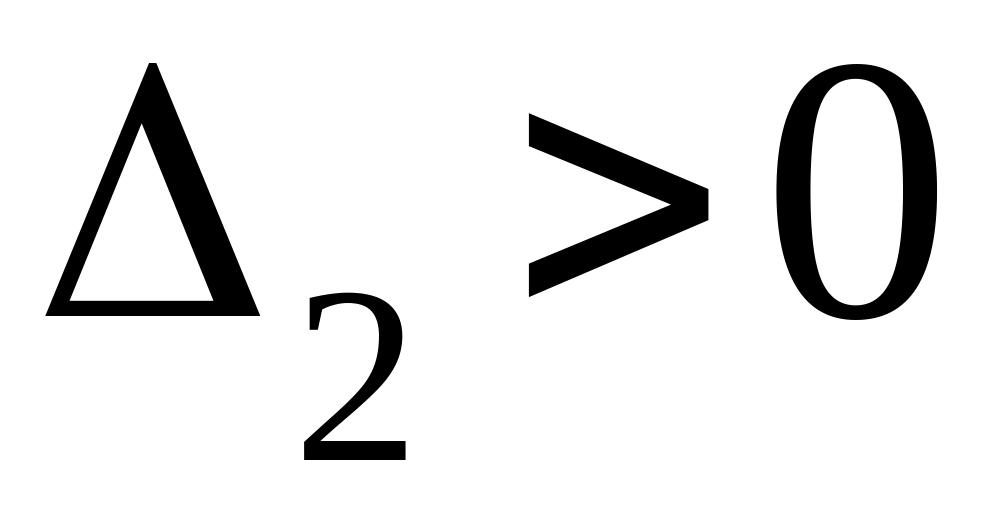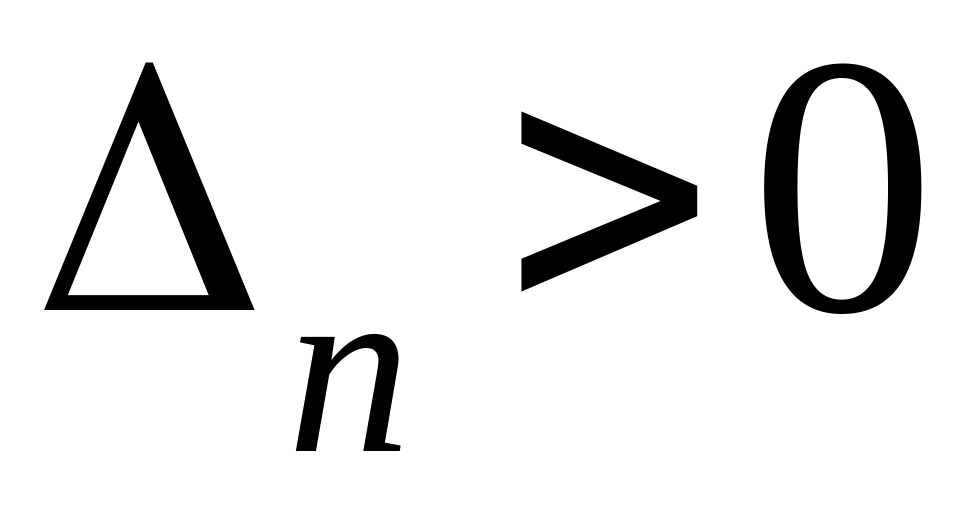
{если хотя бы одно из этих условий не выполнено, то система автоматического управления НЕУСТОЙЧИВА}.