88. Критерий устойчивости (критерий Михайлова)

КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА.

Критерий устойчивости Михайлова относится к частотным критериям и используется для исследования устойчивости замкнутых систем. Рассмотрим замкнутую систему управления структурная схема которой имеет вид

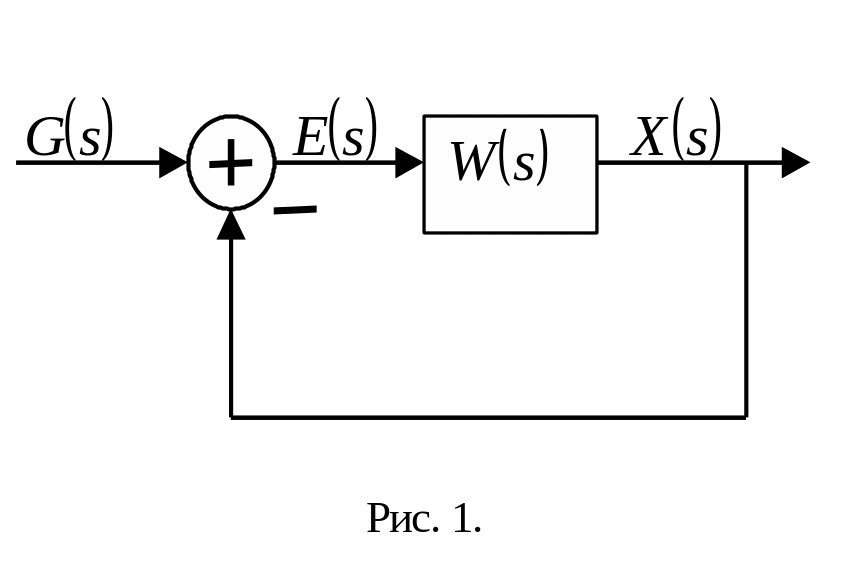
Пусть передаточная функция разомкнутой системы равна

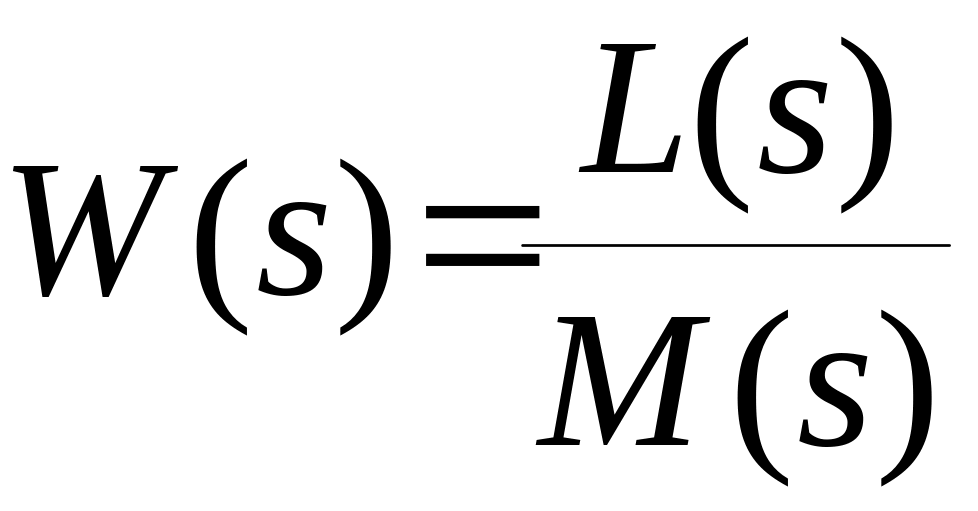
и пусть – степень полинома , – степень полинома .

Передаточная функция замкнутой системы

.

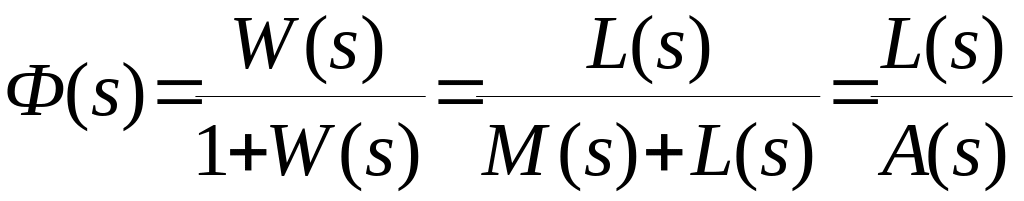Полином - имеем степень -степень полинома

.

Составим характеристический полином замкнутой системы

. (1)

Если подставим в , то получим комплексное число

.

В последнем равенстве выделим действительную и мнимую части комплексного числа:

, (2)

где

. (3)

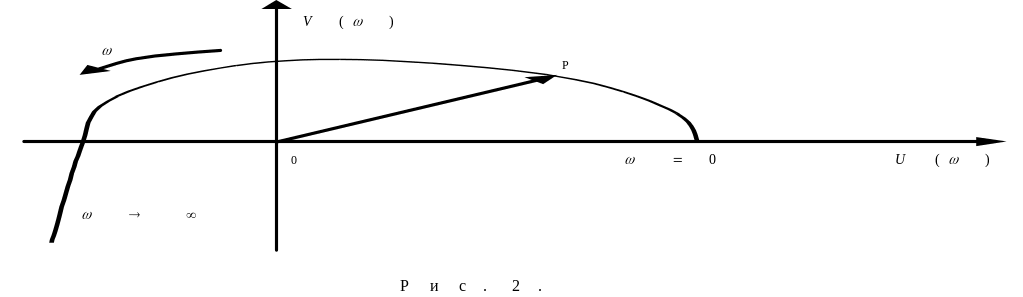
На плоскости и комплексное число изображается вектором (см. рис. 2). При из изменении частоты от 0 до вектор изменяется по величине и направлению. Конец вектора в комплексной плоскости описывает некоторую кривую, которая называется годографом Михайлова.

Формулировка критерия Михайлова.

Для того, чтобы замкнутая система автоматического управления была устойчива, необходимо и достаточно чтобы годограф Михайлова при изменении частоты от 0 до , начинался при на вещественной положительной полуоси, обходил последовательно квадрантов координатной плоскости против часовой стрелки, где - порядок характеристического полинома.

Заметим, что для устойчивых систем автоматического управления годограф Михайлова начинается при на вещественной положительной полуоси, поскольку, поскольку все коэффициенты характеристического полинома положительны и .

Кроме того, для устойчивых систем фаза с ростом частоты должна возрастать монотонно, т.е. вектор должен поворачиваться только против стрелки, поскольку с ростом частоты монотонно возрастают имеющие одинаковые знаки фазы элементарных векторов ,являющиеся слагаемыми вектора .

Кривая Михайлова для устойчивых систем всегда плавную спиралевидную форму, причём конец её ( ) уходит в бесконечность в том квадранте координатной плоскости, номер которого равен степени характеристического полинома.

Типовые кривые Михайлова для устойчивых систем, имеющих характеристический полином степеней , , , и представлены на рисунке 3 ( - во всех случаях приняты одинаковыми).

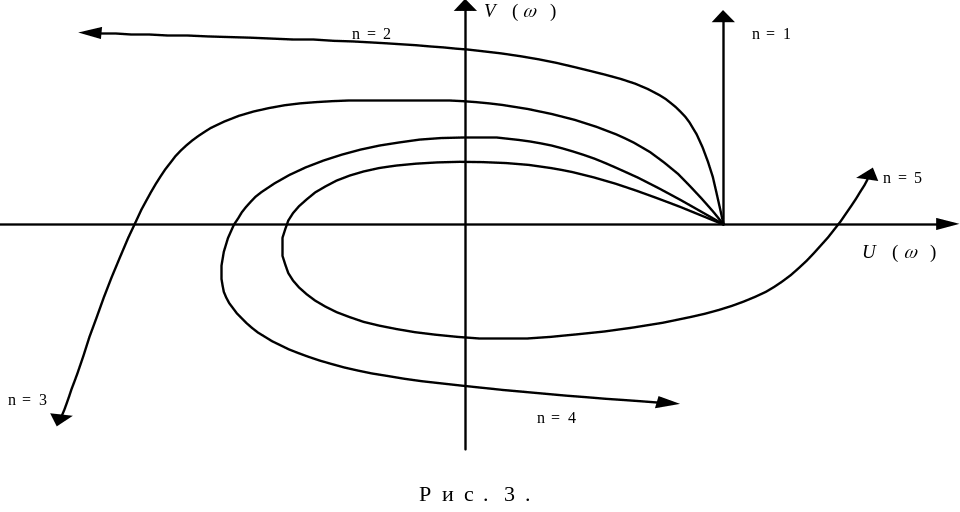
Признаком неустойчивости системы является нарушение числа и последовательности пройденных кривой Михайлова квадрантов координатной плоскости, вследствие чего угол поворота вектора оказывается меньшим, чем .

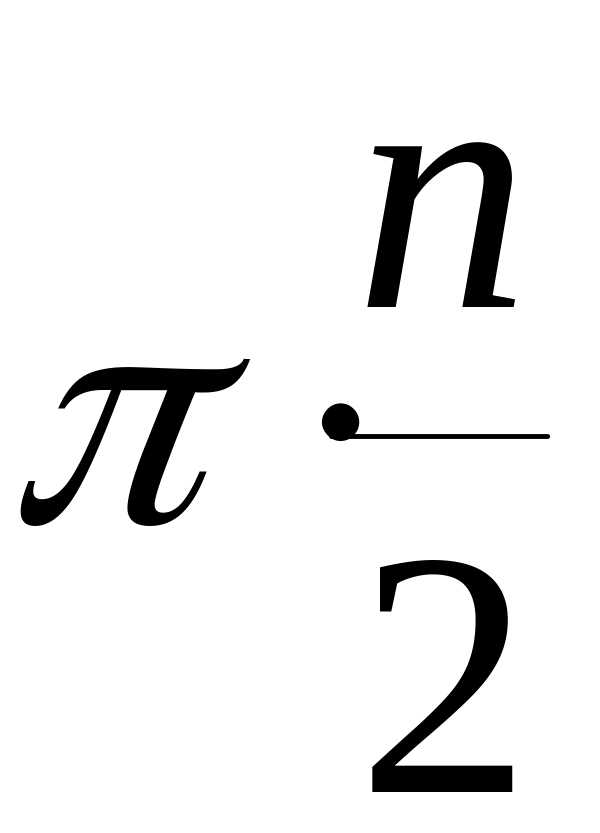Примеры годографов Михайлова для неустойчивых систем:

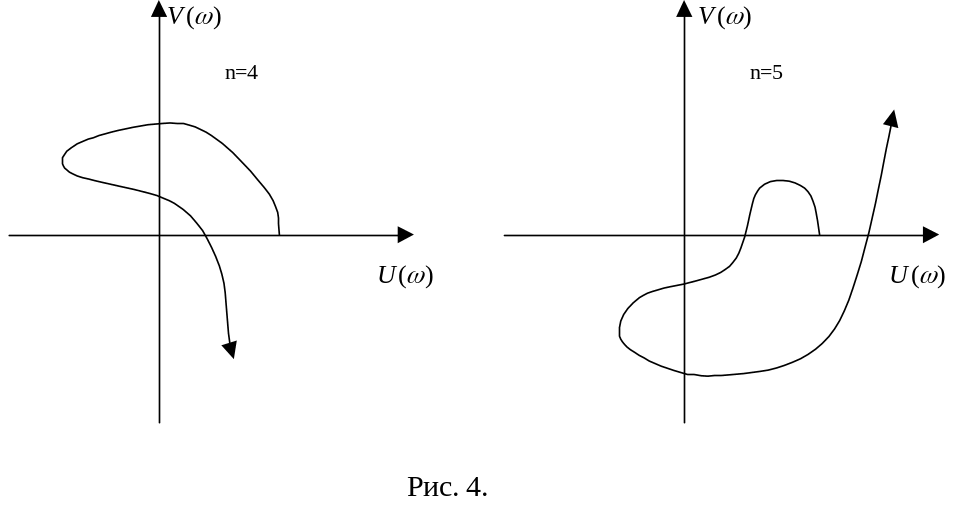
Другая формулировка критерий устойчивости Михайлова.

Система автоматического управления устойчива тогда и только тогда, когда уравнения и имеют все действительные и перемежающиеся корни, причём общее число этих корней равно порядку характеристического уравнения и при выполняется неравенства и .

Устойчивая система:

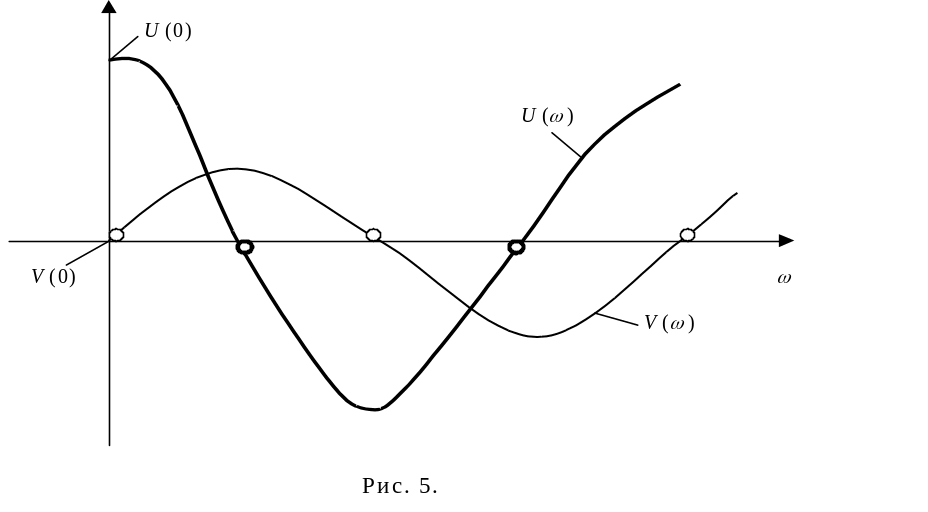
Неустойчивая система:

Это условие устойчивости системы получило также название условие перемежаемости корней.

Правило исследования устойчивости систем автоматического управления с помощью критерия Михайлова. Для исследования устойчивости линейных систем автоматического управления с помощью критерия Михайлова надо:

1. Преобразовать структурную схему исследуемой системы к расчётной структурной схеме

и определить передаточную функцию разомкнутой системы .

2. По передаточной функции разомкнутой системы получить передаточную функцию замкнутой системы

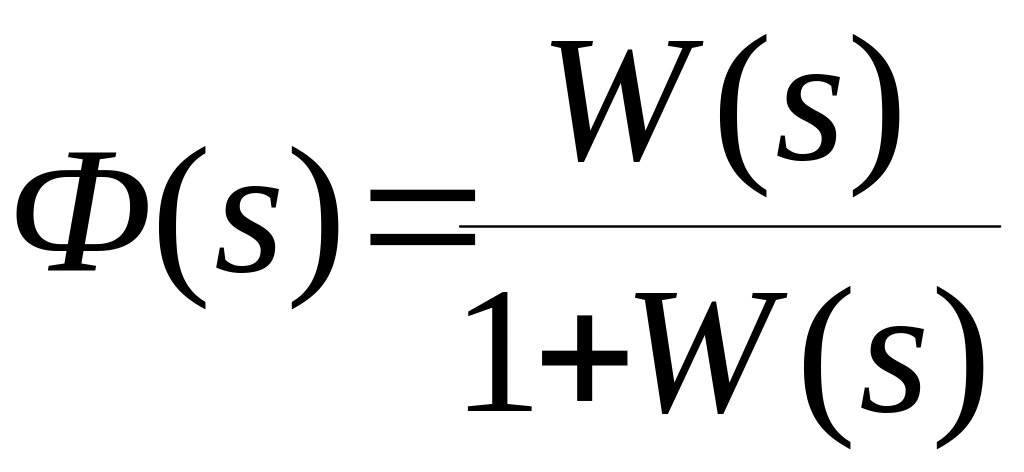
и вычислить характеристический полином замкнутой системы

.

3. В характеристическом полиноме подставить

и выделить в комплексном числе действительную и мнимую части

.

4. Используя полученные выражения для и строим годограф Михайлова, изменяя значения частоты от 0 до .

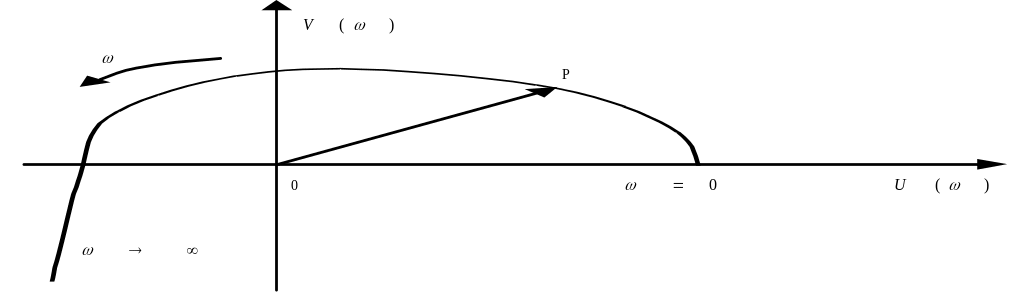
5. Используя критерий Михайлова, по построенному годографу определяем устойчивость системы управления.

Пример. С помощью критерия Михайлова определить устойчивость замкнутой системы с передаточной функцией

; , .

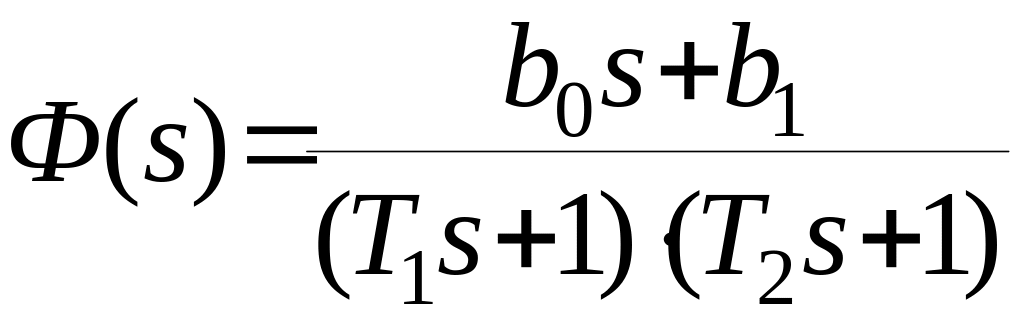Решение. Характеристический полином замкнутой системы:

;

;

;

; .

; .

, .

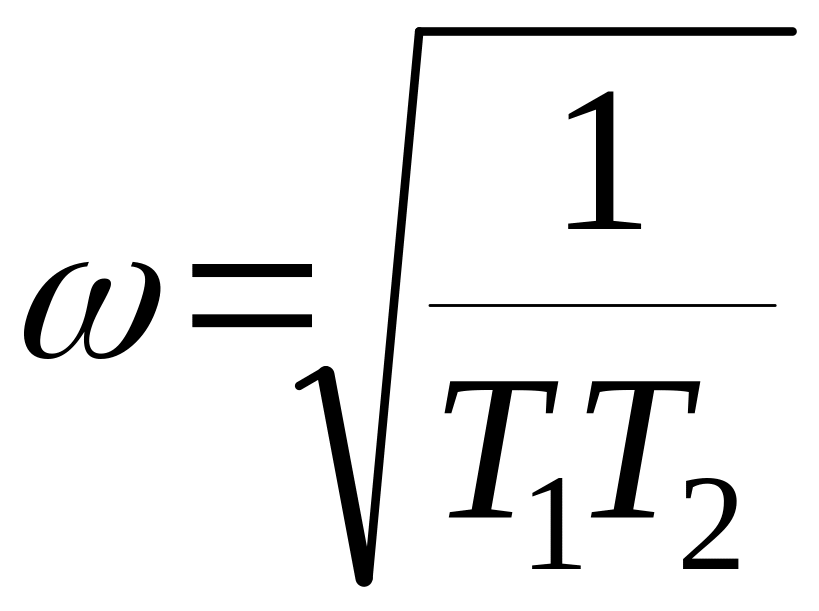Годограф Михайлова.

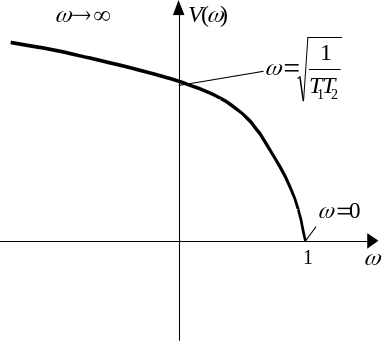
Условие перемежаемости корней:

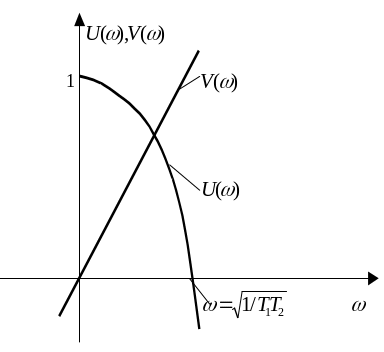
Система устойчива.

Определение границ устойчивости.

Характеристический полином замкнутой системы автоматического управления

.

Система автоматического управления будет находиться на границе устойчивости, если характеристический полином замкнутой системы имеет пару чисто мнимых корней , , а остальные корня имеют отрицательные действительные части.

Подставим в характеристический полином и выделим действительную и мнимую части комплексного числа :

.

(т.к. , то считаем, что это корень характеристического уравнения).

Если система находится на границе устойчивости, то годограф Михайлова для системы проходит через начало координат (см. рис. 7).

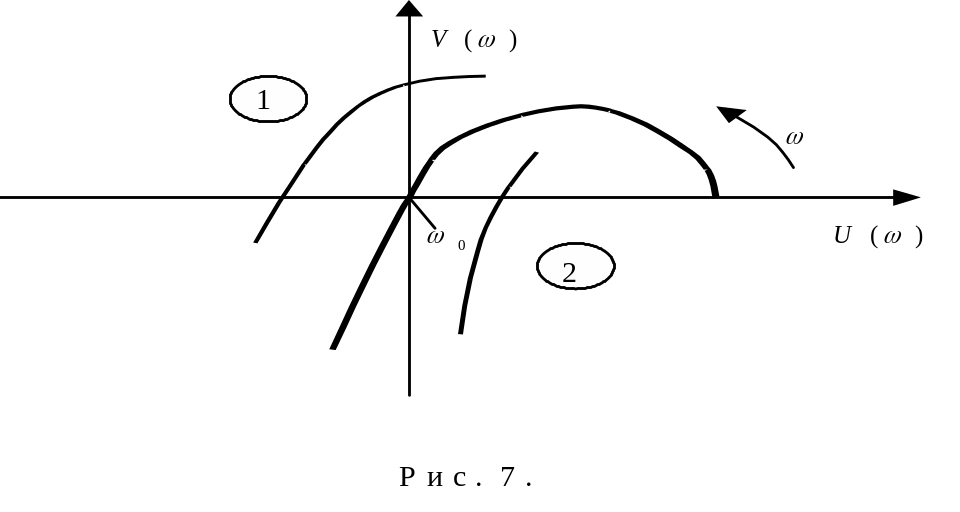
Решение системы уравнений , позволяет установить взаимосвязь параметров замкнутой системы и частоты гармонических колебаний , для случая, когда система будет находиться на границе устойчивости. Если при изменении параметров годограф пойдёт так, как показано на рисунке (кривая 1), то система будет устойчивой, если так как на кривой 2 – то система будет неустойчивой.