78. Что такое импульсная, переходная и частотная характеристики сау? Как они получаются? Их характерные параметры.
78. Что такое импульсная, переходная и частотная характ-ки сау? Как они пол-ся, их осн. Параметры.
1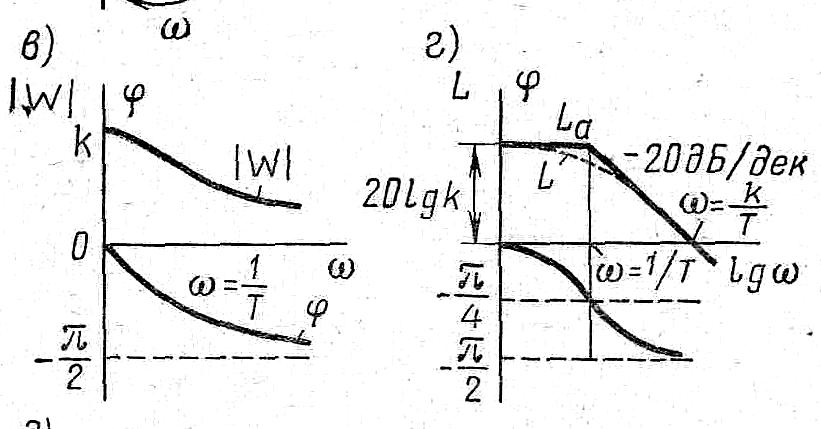
).Импульсн.
переходн. ф-ция (хар-ка)
h’(t)
– производ-я от временной переходной
ф-ции h(t)
и относ-ся к временным характ-м линейн-х
систем. В.х. – графич-е изобр-е процесса
измен-я вх. вел-ны ф-ции врем-ни при
переходе из одного равовесн. сост-я в
др-ое в рез-те поступл-я на вх. некоторого
типового возд-вия (за тип. возд. приним.
ед. ступень).
h(t)=y(t) при X(t)=σ(t): Н(р)=Y(р), σ(р)=1/р=Х(р), Н(р)=W(р) * 1/р, h(t)=L – 1 [W(р)/p]. h’(t)=y(t) при X(t)=δ(t): H’(р)=Y(р), δ(р)=1=Х(р), Y(р)=W(р)X(р), h’(t)=L – 1 [W(р)].
2).Част. хар-ка. Если на вх. лин-ой сист-мы подать синусид-ные гармон-е колеб-я с пост. част-ой и амплит-ой Хвх = Х0 sin wt, то после затух-я перех-х проц-в на вых. возникают синусоид-е колеб-я с той же част-ой, но с др. амплит-ой и сдвинут-е по фазе относит-но вх. сигнала: Yвых = Y0 sin(wt+φ). В комплексн. виде: Y(jw)=Y0(w) e j(wt+φ) – вых., Х(jw)=Х0(w) e jwt – вх. Y(jw)/ Х(jw)= (Y0(w)/ Х0(w)) e jφ(w) =W(jw) – это есть комплексная частотн. передат-я ф-ция. В разл. формах записи: W(jw)=Р(w) +jQ(w), W(jw)=A(w) e jφ(w) , где Р(w)- действит., Q(w)- мнимая части компл-ой ф-ции; A(w), φ(w) – модуль и аргумент част-ой ф-ции. Геометр-ое место концов векторов компл. част-ой ф-ции при изменню частоты от 0 до бескон-ти наз амплитудно –фазовой част-ой характ-ой (АФЧХ), а графики, постр-е в ф-ции частоты, наз. частотн.характ-ми. A(w)- АЧХ, φ(w)- ФЧХ, котор. в практич работах изображ. в логарифмич. масштабе: логариф-кая единица ослаб-я или усил-я мощн-ти при прохожд-и сигнала ч-з к-либо устр-во при выраж-нии десятичныи логар-м величины отношения мощн-ти на вых. к мощн. на вх. наз. бел=lg (P вых/Pвх) = lg (А вых/Авх)2 =2 lg (Авых/Авх). На практ. исп-ся 1 децебел(дцБ) =0,1бел. Отс. 10*2 lg (Авых/Авх)=20lg A(w)= G(w) ЛАЧХ (логарифм. ампл-част. хар-ка).
80. Критерии устойчивости сау. Краткая характеристика. Области применения.
80. Критерии устойчивости САУ. Краткая характеристика. Область применения.
Критерий устойчивости Гурвица.
Составляется определитель Гурвица. Условия устойчивости заключается в требовании положительности определителя Гурвица и всех его диагональных миноров. Этот критерий применяется при полиноме порядка 3,4.
Критерий устойчивости Найквиста.
Если разомкнутая цепь устойчива, условия устойчивости замкнутой САУ сводятся к требования АФЧХ в разомкнутой цепи не охватывала точку (-1;j0).
Критерий устойчивости Михайлова
Система устойчива, если гадограф А(jw) начинается на действительной положи тельной полуоси, огибает против часовой стрелки начало координат проходя последовательно n квадрантов, где n – порядок системы.
81. Алгебраические критерии устойчивости схем автоматического управления.
81. Алгебраические критерии устойчивости схем автоматического управления.
Необходимым условием работоспособности системы автоматического регулирования является ее устойчивость. Под устойчивостью понимают свойство системы восстанавливать состояние равновесия, из которого она была выведена под влиянием возмущающих факторов, после прекращения действия этих факторов. Критерии устойчивости. На практике для определения устойчивости системы автоматического регулирования используют критерии устойчивости, т. е. правила, с помощью которых можно определить, устойчива ли система, не прибегая к решению дифференциальных уравнений.
Алгебраический критерий (Рауса — Гурвица) позволяет судить об устойчивости замкнутой системы по коэффициентам ее характеристического уровня, которым является знаменатель передаточной функции. Необходимые и достаточные условия устойчивости системы определяются различными соотношениями коэффициентов в зависимости от порядка системы.
Критерий устойчивости Найквиста позволяет судить об устойчивости замкнутой системы автоматического регулирования по амплитудно-фазовой характеристике разомкнутой системы. Критерий устойчивости применим, в частности, для систем, устойчивых в разомкнутом состоянии.
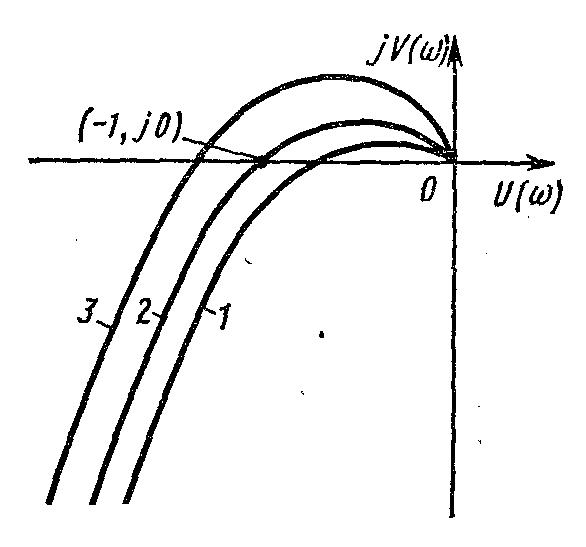
Рис. 37. Амплитудно-фазовые характеристики разомкнутых систем:
1 — система устойчивая; 2 — система на границе устойчивости; 3 — система неустойчивая
Замкнутая система будет устойчива в том случае, если устойчива разомкнутая система и ее амплитудно-фазовая характеристика не охватывает точку с координатами (- 1, j0), называемую критической (рис. 37). При отсутствии местных обратных связей разомкнутая система всегда устойчива, если состоит из устойчивых звеньев. При наличии местных обратных связей система может оказаться неустойчивой в разомкнутом состоянии.
Апериодическое звено. Характеристики.
82. Апериодическое звено (АЗ). Характеристики.
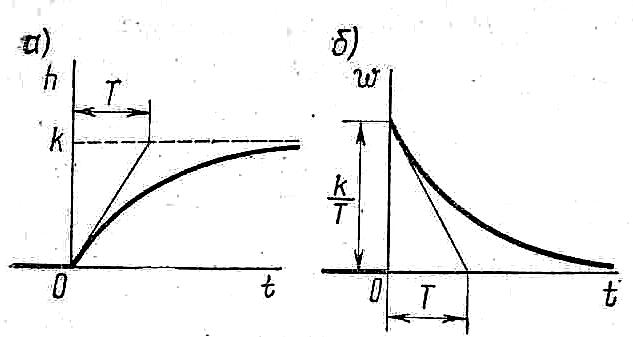
В ТАУ к линейному типовому звену относят АЗ 1 порядка, оно принадлежит к позиционной группе типовых звеньев, при кот-ой при подаче на вход звена пост. величины, на вых. устан-ся с теч-м вр-ни пост. вел-на. Физ. аналог.:
T dy/dt + y = kx – ур-ие звена
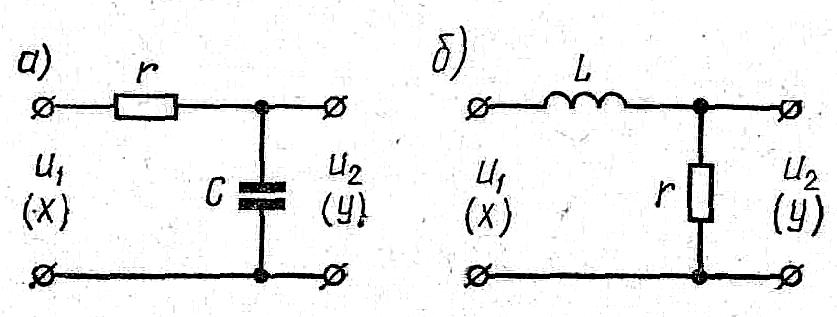
W(p) = k/(1+pT)
h(t) = k(1-e-t/T)l0(t)
w(t) = dh/dt = ke-t/Tl0(t)
Частотные критерии устойчивости.
83. Частотные критерии устойчивости.
Частотные критерии устойчивости позволяют судить об устойчивости систем автоматического управления по их частотным характеристикам. Эти критерии являются графоаналитическими и получили широкое распространение, так как позволяют сравнительно легко исследовать устойчивость систем высокого порядка, а так же имеют простую геометрическую интерпретацию и наглядность.
Критерий устойчивости Михайлова основан на связи характера переходного процесса системы с амплитудой и фазой вынужденных колебаний, устанавливающихся в системе при синусоидальном воздействии. Анализ устойчивости системы этим методом сводится к построению по характеристическому многочлену замкнутой системы (знаменатель передаточной функции) комплексной частотной функции, по виду которой можно судить об устойчивости системы.