Структура производства с уменьшением нормы прибыли
Предположим, что предприятие выпускает телевизоры, стерео- и акустические системы, используя один склад комплектующих. В связи с ограниченностью запаса необходимо найти оптимальное соотношение объема выпуска изделий.
Эта модель включает данные по нескольким изделиям, в которых использованы общие комплектующие. Каждому изделию соответствует своя норма прибыли. Запас комплектующих ограничен, и задача состоит в определении каждого вида изделий для получения наибольшей прибыли.
Данные задачи представлены в таблице:
Наименование |
Телевизор |
Стерео |
Ак .сист. |
||
|
|
Количество-> |
100 |
100 |
100 |
Наим.изд. |
Склад |
Использ. |
|
|
|
Шасси |
450 |
200 |
1 |
1 |
0 |
Кинескоп |
250 |
100 |
1 |
0 |
0 |
Динамик |
800 |
500 |
2 |
2 |
1 |
Блок пит. |
450 |
200 |
1 |
1 |
0 |
Элек. плата |
600 |
400 |
2 |
1 |
1 |
Прибыль по видам изделий, т. руб |
4 732р. |
3 155р. |
2 208р. |
||
Прибыль всего: |
10 095р. |
||||
!!! В ранее созданной книге создайте новый лист и назовите его "Структура производства". |
Данные задачи занесите на лист Excel в следующем виде:
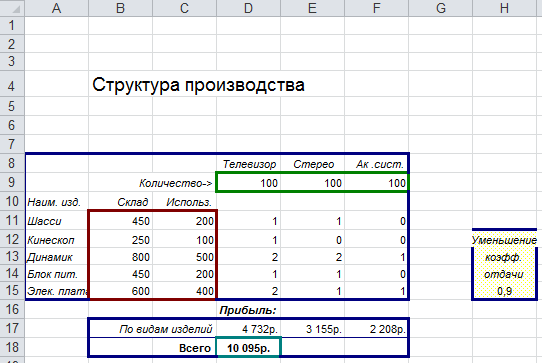
!!! Перенесите данные из таблицы на лист MS Excel без изменений |
Ниже приведенные строки будет содержать формулы.
!!! Занесите следующие формулы в строку формул fx соответствующей ячейки или непосредственно в саму ячейку. |
Ячейка |
Формула |
D17 |
= 75*МАКС(D9;0)^$H$15 |
E17 |
=50*МАКС(E9;0)^$H$15 |
F17 |
= 35*МАКС(F9;0)^$H$15 |
D18 |
= СУММ(D17:F17) |
С11 |
=$D$9*D11+$E$9*E11+$F$9*F11 |
С12 |
=$D$9*D12+$E$9*E12+$F$9*F12 |
С13 |
=$D$9*D13+$E$9*E13+$F$9*F13 |
С14 |
=$D$9*D14+$E$9*E14+$F$9*F14 |
С15 |
=$D$9*D15+$E$9*E15+$F$9*F15 |
Используйте инструмент Поиск решения . В нашем случае окно поиска решения должно иметь вид:
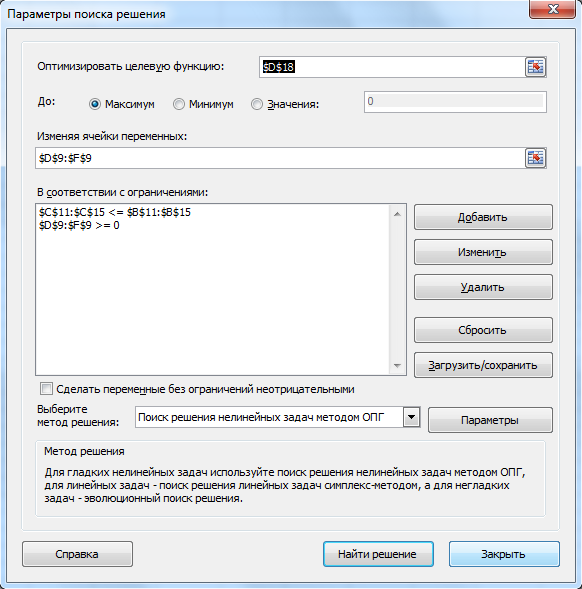
!!! Нажмите кнопку Найти решение для получения решения задачи |
Ваш результат должен выглядеть следующим образом. Если Ваши результаты не соответствуют представленному решению – проверьте правильность ограничений и установленную целевую ячейку.
В формулу прибыли на изделие в ячейках D17:F17 входит коэффициент ^H15, учитывающий уменьшение прибыли с ростом объема. В H15 содержится 0,9, что делает задачу нелинейной. Изменение H15 на 1,0 (если прибыль не зависит от объема производства) и повторный запуск процесса поиска решения даст другое решение, отличное от оптимального решения, найденного ранее. Данное изменение делает задачу линейной.
Просмотрите оборудование для лабораторной работы и порядок ее выполнения перейдя по ссылке.