Простейшая задача линейного программирования
Рассмотрим решение задачи линейного программирования на следующем примере:
Целевая функция:
Z 4 x1 + 6 x2 min
Ограничения:
|
3x1 + x2 9 x1 +2 x2 8 x1 +6 x2 12 x1 0, x2 0 |
Подготовка рабочей таблицы на листе Excel
Для решения задачи необходимо подготовить исходную таблицу на рабочем листе Microsoft Excel. Для этого
!!! Создайте новую книгу MS Excel «Линейное программирование <ФИО студента>» |
Переименуйте лист 1, на котором Вы будете работать, для этого щелкните по нему правой кнопкой мыши и в открывшемся меню выберете Переименовать. Введите с клавиатуры название "Простейшая задача линейного программирования". Подготовьте на листе 1 MS Excel рабочую таблицу. Она должна выглядеть так:
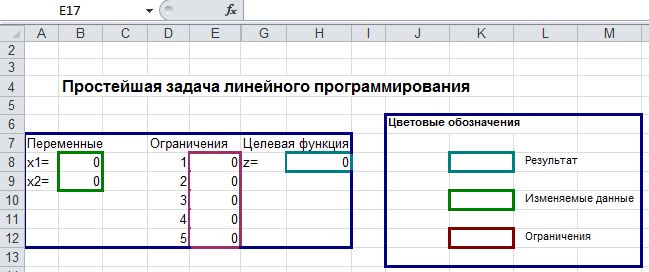
В данном случае ячейки B8 и B9 пусты, так как в них Excel позже разместит оптимальное базовое решение.
!!! В ячейки E8:E12 занесите формулы, соответствующие ограничениям линейной модели |
Эти формулы будут выглядеть так:
Ячейка |
Формула |
E8 |
=3*B8+B9 |
E9 |
=B8+2*B9 |
E10 |
=B8+6*B9 |
E11 |
=B8 |
E12 |
=B9 |
!!! В ячейку H8 занесите формулу, соответствующую целевой функции, т.е.: =4*B8+6*B9 |
Работа с инструментом Поиск решения
Теперь, чтобы решить задачу линейного программирования нужно воспользоваться инструментом Поиск решения.
!!! Откройте окно поиска решения и установите в нем целевую ячейку, укажите изменяемые ячейки и внесите ограничения. |
В данном случае целевой ячейкой является H8, она стремится к минимальному значению. Изменяемые ячейки: B8 и B9.
Добавьте ограничения. Для этого нажмите кнопку Добавить. Ограничения добавляются в соответствии с исходной линейной моделью. Так как формулы ограничений были записаны в ячейки Е8:Е12, значит, они будут иметь вид.
Ячейка |
знак |
Ограничение |
E8 |
>= |
9 |
E9 |
>= |
8 |
E10 |
>= |
12 |
E11 |
>= |
0 |
E12 |
>= |
0 |
Всего ограничений будет пять, как и в исходной линейной модели.
!!! Нажмите кнопку Найти решение, чтобы получить решение задачи |
MS Excel предложит сохранить найденное решение в таблице и создать отчет.
Выберите Тип отчета «Результаты». Таблица с решениями должна выглядеть следующим образом. Если ваши результаты не соответствуют приведенному решению – проверьте правильность ограничений и установленную целевую ячейку.
Транспортная задача
В простейшей постановке транспортная задача представляет собой определение минимальных затрат на перевозку некоторой однородной продукции из пунктов отправления (от поставщиков или производителей) в пункты назначения (потребителям).
Данная задача решает проблему доставки товаров с трех заводов на пять региональных складов. Считается, что товары могут доставляться с любого завода на любой склад. Очевидно, что стоимость доставки на большее расстояние будет большей. Требуется определить объемы перевозок между каждым заводом и складом, в соответствии с производственными потребностями складов и заводов, при которых транспортные расходы будут минимальными.
В обычном виде данные задачи представлены в таблице.
потребители поставщики |
Казань |
Рига |
Воронеж |
Курск |
Москва |
Запасы |
Белоруссия |
4 |
2 |
3 |
1 |
2 |
100 |
Украина |
6 |
5 |
3 |
4 |
3 |
125 |
Литва |
6 |
4 |
5 |
2 |
3 |
75 |
Потребность |
55 |
65 |
50 |
75 |
55 |
300 |
!!! В ранее созданной книге создайте новый лист и назовите его "Транспортная задача". |
Структура транспортной задачи на листе MS Excel будет следующей.
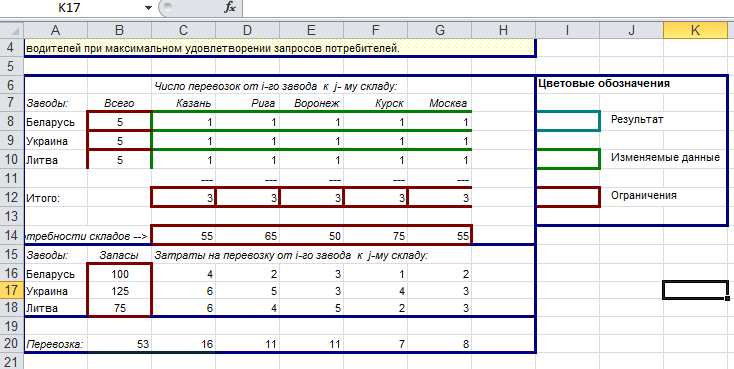
Для того, чтобы сформировать такую таблицу выполните следующие действия:
|
|
|
Далее для формирования ограничений необходимо ввести ряд формул. Для этого, формально примем, что число перевозок от i-го завода к j-му складу равно 1, так как эти данные в задачи являются изменяемыми. Поэтому:
!!! Внесите в ячейки С8С10:G8G10 значение 1 |
!!! В ячейку В8 внесите формулу =СУММ(C8:G8). |
Затем наведите курсор мыши в нижний правый угол этой ячейки и, после появления значка + , растяните рабочую область ячейки на столбец В8:В10.
!!! В ячейку С12 внесите формулу =СУММ(C8:С10). |
Затем наведите курсор мыши в нижний правый угол этой ячейки и, после появления значка + , растяните рабочую область ячейки на строку C8:G8.
!!! В ячейку С20 внесите формулу =C8*C16+C9*C17+C10*C18 |
Затем наведите курсор мыши в нижний правый угол этой ячейки и, после появления значка +, растяните рабочую область ячейки на строку C20:G20.
И последняя формула сформирует целевую ячейку. Для ее создания:
!!! В ячейку С20 внесите формулу =СУММ(C20:G20) |
Затем в окне поиск решения Данные/Поиск решения установите целевую ячейку В20, которая стремится к минимальному значению. Укажите изменяемые величины (ими будут ячейки C8:G10) и внесите ограничения, приведенные в следующей таблице.
Ячейка |
знак |
Ограничение |
В8:В10 |
<= |
В16:В18 |
C12:G12 |
>= |
C14:G14 |
C8:G10 |
>= |
0 |
!!! Нажмите кнопку Найти решение, чтобы получить результаты задачи |
Результаты поиска решений можно просмотреть после появления окна Результаты поиска решения. Если все ячейки содержат числовые данные, целевая ячейка не равна 0 и нет сообщений об ошибке, то задача решена . В этом случае выберете команду Сохранить найденное решение. Если решение сохранено, но оно не удовлетворяет каким-либо требованиям, вернуть исходные данные можно заменив значения в ячейках С8С10:G8G10 на 1.
Ваш результат должен иметь приведенный здесь вид. Если ваши результаты не соответствуют решению – проверьте правильность ограничений и установленную целевую ячейку.