Практичне заняття та варіанти завдань №5

РОЗРАХУНОК ПРУЖИНЕННЯ ПРОФ1ЛЬНИХ ЗАГОТОВОК ПРИ ЗГИНАННІ

Мета роботи: 1. Ознайомлення з технологією згинання профільних заготовок.

2. Оволодіння методикою розрахунку.

1. Теоретична частика

Для виготовлення кілець та секторів кілець в профілів застосовую різноманітні методи згинання (див. рис. 1).

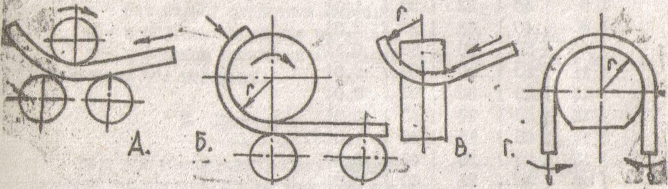
а - прокатка роликами; б - намотування на оправку, в - у штампі по ділянках;

г - згинання з розтягом

Рис. 1. Засоби згинання:

Радіуси згинання визначають з урахуванням пружинення заготовки. Після розвантаження заготовки радіус збільшується і складає . При згинанні з розтягом пружинення виявляється значно менше.

Виразимо показник пружинення як зміну кривизни:

(1)

У такому формулюванні . Радіуси і . будемо прив'язувати до нейтральної поверхні або до центру ваги перерізу профілю.

Переріз навантаженої заготовки поділений на зони стиснення та розтягу нейтральною лінією I - I (рис. 2). .

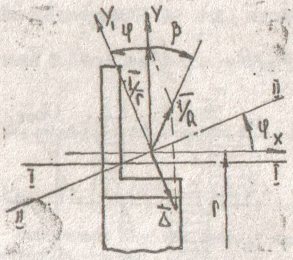
Рис.2. Схема пружинення несиметричного профілю

Початок координат X, розташовується в центрі ваги перерізу. Ось взагалі не збігається з нейтральною лінією I - I, положення останьої залежить від зовнішнього навантаження та може бути визначено інтегруванням напруги згинання на площі перерізу профілю.

,

де - поздовжня сила, у більшості випадків .

Напружений стан приймають лінійним відносно великих радіусів згинання. Зоною пружних деформацій нехтуємо, отже . Якщо використовувати постійне осереднене значення напруження текучості , то виявляється , що при нейтральна лінія поділяє переріз на дві частини рівної площі. Складові зовнішнього згинаючого моменту і урівноважуються моментами внутрішніх сил:

, (2)

Якщо переріз симетричний відносно осі , то . При розвантаженні напруження змінюються, остаточне значення

,

де: - лінійний модуль пружності;

деформації розвантаження вибрані за знаком деформації згинання.

Остаточні напруження (див. рис. 3) самоурівноважені, тобто

, . (3)

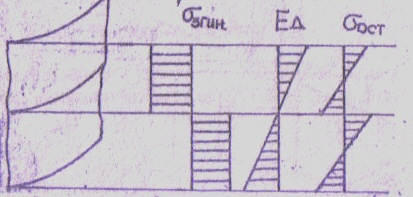
Рис. 3. Напруження у перерізі симетричного профілю

При площина згинання та площина розвантаження не збільшується, , де вісь повернута відносно осі на деякий кут , рівно як і нейтральна лінія розвантаження II - II відносно лінії I - I (див. рис.2) Це пояснюється тим, що обидва складових моменти внутрішніх сил (підінтегральний вирах 2) викликають пружинення - кожний у своєму напрямку, як т1льки порушується и рівноважна з зовнішнім навантаженням.

Показник пружинення є , таким чином, результуючою двох складових (див. рис. 2). Згідно з (1) є різницею векторів та . В результаті пружинення вектор остаточної кривизни не тільки по модулю, але й по напрямку - на кут (див. рис. 2). На практиці це виявляється у розгортанні поперечного перерізу відносно площини кільця (рис. 4).

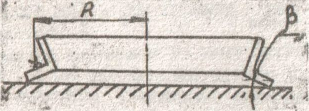
Рис. 4. Неприлягання стінки зігнутого профілю до площини контрольного стола

Для виводу розрахункових формул підставимо у (3) та :

; .

З урахуванням формули та виразів (2) маємо:

;

;

де: , - центральні моменти інерції перерізу;

- відцентровий момент.

Із одержаних рівнянь маємо:

; .

З паралелограму векторів (рис. 2) маємо:

; .