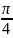3 Результаты работы

В данном разделе мы рассмотрим результаты численного решения задачи при различных углах смачивания, а также определим критическое значение числа Бонда для этих углов.

Далее представлены графики формы поверхности жидкости при различных углах смачивания, а именно: . Также будет представлена сравнительная таблица чисел Бонда вычисленных аналитически и численно.

3.1 Отрыв капли от горизонтальной поверхности

В результате применения алгоритма решения поставленной задачи, мы получили критическое значение числа Бонда для разных углов смачивания, но только для тех, для которых известно точное аналитическое значение.

Угол смачивания	Число Бонда (аналитическое)	Число Бонда (расчетное)
	2.265	2.266245
	4.988	4.9834538
	0.579	0.5766983
1.523	2.407	2.405714

Таблица 1 – Критические значения числа Бонда

Критическое значение числа Бонда вычислялось с точностью 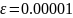. По таблице видно что вычисления верны. Отсюда можно сделать вывод, что алгоритм работает верно.

Представим график иллюстрирующий зависимость числа Бонда критического от угла смачивания.

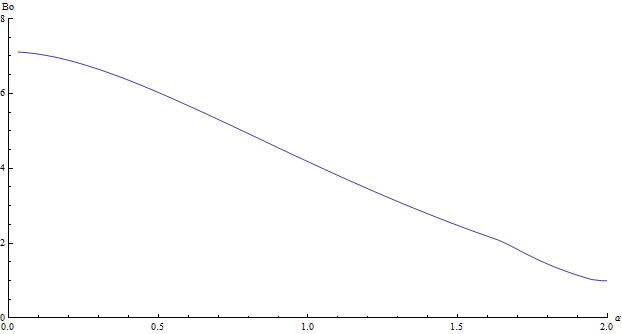
Рисунок 4 – График зависимости числа Бонда от угла смачивания

3.2 Визуализация полученного решения

Представим результаты вычислений на графиках при значениях Бонда близких к числу Бонда, т.е. перед отрывом капли от горизонтальной поверхности.

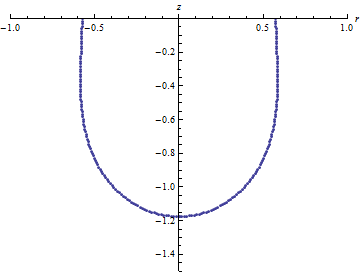
Рисунок 5 – Визуализация решения при

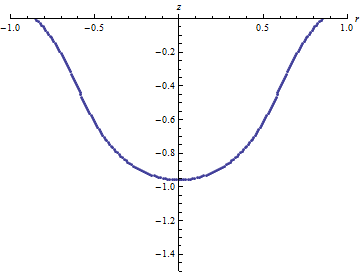
Рисунок 6 – Визуализация решения при

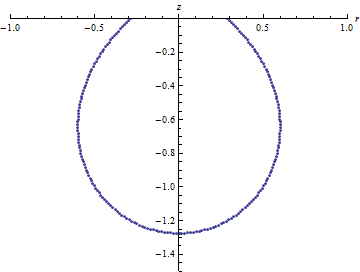
Рисунок 7 – Визуализация решения при

Список использованных источников

1. Polevikov V.K. Methods for numerical modeling of two-dimensional capillary surfaces // Computional Methods in Applied Mathematics. – 2004. –Vol.4, №1. –P. 66-93.

2. Мышкис, А.Д. Методы решения гидромеханики для условий невесомости / А.Д. Мышкис, В.Г. Бабский, М.Ю. Жуков, Н.Д. Копачевский, Л.А. Слобожанин, А.Д. Тюнцов. - Киев: Наукова думка, 1992.

3. В.К. Полевиков. О методах Численного моделирования равновестных капиллярных поверхностей. Дифференциальные уравнения. 1999, T.35, №7. С. 975-981

Приложение а

ClearAll;

n=100;

α=N[3*π/4];

h=1/n;

τ=0.1;

ε=10^-2;

(*н=а0чGа0л;ьLн=о>е5 п?р@и8б1л;и8ж6е5н=и8е5*)

B0=0;(*чGи8сAл;о> Б11о>н=д4а0*)

r1=N[Table[If[i==1,

0,

1/α*Sin[(i-1)/n*α]

],{i,1,n+1}]

];

z1=N[Table[If[i==n+1,

0,

1/α*(Cos[α]-Cos[(i-1)/n*α])],{i,1,n+1}]

];

r=r1;

z=z1;

f1=N[Table[If[i==1,

0,

If[i==n+1,

-Sin[α]/r1[[n+1]],

-(z1[[i+1]]-z1[[i-1]])/2/h/r1[[i]]]

],{i,1,n+1}]

];

C1=2*α;

F1=Table[f1[[i]]+C1,{i,1,n+1}];

LN=(4*π*(2+Cos[α])*(Sin[α/2])^4/(3*α^3))^-1/3;

list=List[ListPlot[Table[{r1[[i]],z1[[i]]},{i,1,n+1}]]];

met2=0;

(*а0л;г3о>р@и8тBм<*)

ListLinePlot[Table[{r1[[i]],z1[[i]]},{i,1,n+1}],AspectRatio->1/(1/1.5),PlotRange->{{0,1},{0,-1.5}}]

(*Print["init rN=",r1];

Print["init zN=",z1];*)

B0=0.5;

(*в2ыKчGи8сAл;е5н=и8е5 r*)

While[B0<=0.58,

While[True,met=0;met1=0;

L1=LN;

prevR1=r1;

prevZ1=z1;

prevF1=F1;

prevLN=LN;

(*Print["L=",N[LN]];

Print["C=",C1];

Print["f=",f1];*)

b=Table[

If[i==n+1,

h*Cos[α]-h²*F1[[i]]*Sin[α]/2,

-(((r1[[i+1]]-2*r1[[i]]+r1[[i-1]])*(τ-1)/(h²*τ)+(z1[[i+1]]-z1[[i-1]])/(2*h)*F1[[i]])*τ*h²)],

{i,2,n+1}];

A=Table[

If[j==i-1,

1,

If[j==i,

-2,

If[j==i+1,

1,

0

]]],{i,1,n},{j,1,n}];

A[[n]][[n-1]]=-1;

A[[n]][[n]]=1;

temp=LinearSolve[A,b];

rN=Table[If[i==1,0,temp[[i-1]]],{i,1,n+1}];

(*Print["rN=",rN];*)

(*в2ыKчGи8сAл;е5н=и8е5 z*)

b=Table[

If[i==1,

h²*F1[[i]]/2,

-(((z1[[i+1]]-2*z1[[i]]+z1[[i-1]])*(τ-1)/h²/τ-(r1[[i+1]]-r1[[i-1]])/2/h*F1[[i]])*τ*h²)],

{i,1,n}];

A=Table[

If[j==i-1,

1,

If[j==i,

-2,

If[j==i+1,

1,

0

]]],{i,1,n},{j,1,n}];

A[[1]][[1]]=-1;

temp=LinearSolve[A,b];

zN=Table[If[i==n+1,0,temp[[i]]],{i,1,n+1}];

(*Print["zN=",zN];*)

(*п?е5р@е5сAчGе5тB п?е5р@е5м<е5н=н=ыKхE*)

(*LN=N[(π/4*(‘™

˜UnderoverscriptBox[™∨, ™i = 3, ™n]™(™(zN[™[i]] + zN[™[i - 1]])*™(rN[™[i]] + rN[™[i - 1]])*™(rN[™[i + 1]] + rN[™[i]] - rN[™[i - 1]] - rN[™[i - 2]])/2))+π/2*h*((zN[[1]]+zN[[2]])*(rN[[1]]+rN[[2]])+(zN[[n]]+zN[[n+1]])*(rN[[n]]+rN[[n+1]])*Cos[α]))^(-1/3)];*)

I1=0;

For[i=2,i<n,i++,

I1=I1+(zN[[i-1]]+zN[[i]])*(rN[[i-1]]+rN[[i]])*(rN[[i]]-rN[[i-1]])/4;

];

LN=1/;

C1=(2*Sin[α])/rN[[n+1]]-B0/(π*LN*(rN[[n+1]])²);

f1=Table[If[i==1,0,If[i==n+1,-(Sin[α]/r1[[n+1]]),-B0*LN²*zN[[i]]-(zN[[i+1]]-zN[[i-1]])/(rN[[i]]*2*h)]],{i,1,n+1}];

F1=Table[f1[[i]]+C1,{i,1,n+1}];

(*Print["L=",N[LN]];

Print["C=",C1];

Print["f=",f1];*)

(*п?р@о>в2е5р@к:а0 н=а0 о>сAтBа0н=о>в2к:уC*)

If[met2==0,

For[i=1,i<=n+1,i++,

If[zN[[i]]>0||rN[[i]]<0,

met=1]

];

For[i=1,i<=n+1,i++,

If[Norm[(zN[[i]]-z1[[i]])/τ]>ε||Norm[(rN[[i]]-r1[[i]])/τ]>ε,

met1=1]

];

];

met2=0;

r1=rN;

z1=zN;

If[met==1,Break[]];

If[met1==0,Break[]];

];

met2=1;

If[met==1,r1=prevR1;

z1=prevZ1;

zN=z1;

rN=r1;

F1=prevF1;

LN=prevLN;

];

(*list=Append[list,ListLinePlot[

Table[{r1[[i]],z1[[i]]},{i,1,n+1}],AspectRatio->1/(1/1.5),PlotRange->{{0,1},{0,-1.5}}]];*)

(*Print[Show[list]];*)

B0=B0+0.001;

Print[B0];

]

ListLinePlot[

Table[{r1[[i]],z1[[i]]},{i,1,n+1}],AspectRatio->1/(1/1.5),PlotRange->{{0,1},{0,-1.5}}]