МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Факультет прикладной математики и информатики

Кафедра вычислительной математики

ГУСЕВ АЛЕКСАНДР ВИКТОРОВИЧ

Численное решение задачи о равновестной форме капилярных поверхностей

Лабораторная работа

студента 4 курса 5 группы

Преподаватель Будник Анатолий Михайлович доцент кафедры выч. мат., Канд. физ.-мат. наук

Минск 2012

Содержание

1 Математическая модель задачи о форме поверхности жидкости 3

1.1 Постановка задачи 3

1.2 Параметрическое уравнение свободной поверхности 3

1.3 Постановка задачи для итерационно-разностного метода 4

1.4 Замена переменных 5

2 Итерационно-разностный метод 5

2.1 Аналитическое решение при Bo=0 5

2.2 Итерационно-разностный метод. Вычислительный алгоритм 6

3 Результаты работы 8

3.1 Отрыв капли от горизонтальной поверхности 8

3.2 Визуализация полученного решения 9

Список использованных источников 11

ПРИЛОЖЕНИЕ А 12

1 Математическая модель задачи о форме поверхности жидкости

В данном разделе рассматривается постановка задачи а также строится математическая модель.

1. Постановка задачи

Рассмотрим плоскую горизонтальную поверхность, снизу которой расположена капля жидкости, объем которой увеличивается. Параметры системы изменяются постепенно и достаточно медленно для того, чтобы в каждый момент времени свободную поверхность жидкости можно было считать равновесной.

Задача состоит в том чтобы описать форму поверхности жидкости при различных значениях угла смачивания и числа Бонда, а также определить критический значения числа Бонда при которых происходит отрыв капли от горизонтальной поверхности. В данной задаче рассматривается симметричная капля, основанием которой является окружность.

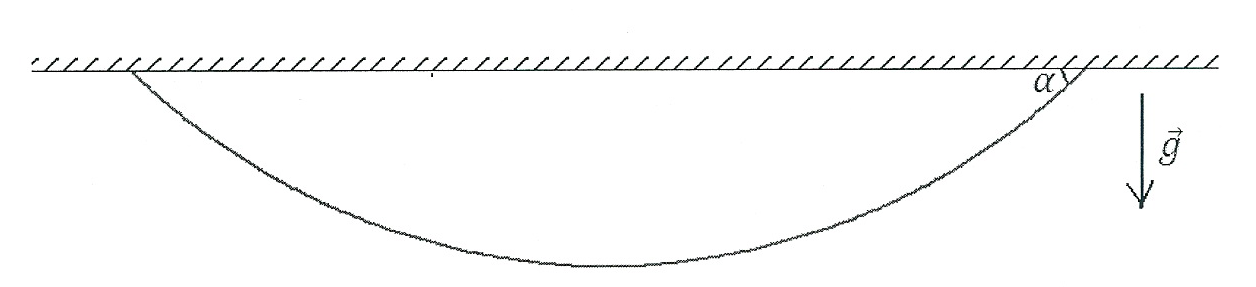
Рисунок 1 – Задача об отрыве капли

1.2 Параметрическое уравнение свободной поверхности

Так как основанием капли является окружность то поверхность жидкости можно рассматривать как поверхность вращения с осью вращения совпадающей с осью симметрии капли. В следствии этого будем рассматривать цилиндрическую систему координат. Так как мы рассматриваем каплю как поверхность вращения, то можно пренебречь одной из координат, а именно, углом поворота. Поэтому получаем двумерную обычную прямоугольную систему координат.

Выберем начало координат на плоской горизонтальной поверхности в точке пересечения горизонтальной поверхности с осью симметрии капли. Ось OZ совпадает с осью симметрии капли и направлена против вектора ускорения свободного падения , а ось OR направлена вдоль горизонтальной плоскости (рис.2).

Пусть S – длина дуги неизвестной линии меридиана, изменяется в пределах от 0 до l.

Значение S=0 длина дуги принимает в вершине капли и S=l в точке, где линия меридиана капли касается горизонтальной плоскости.

Форма дуги поверхности капли описывается параметрическими функциями R(S) и Z(S).

Для поверхности капли имеем уравнения с граничными условиями:

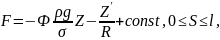(1)

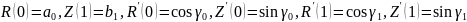(2)

где – плотность, 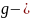ускорение свободного падения, 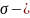коэффициент поверхностного натяжения.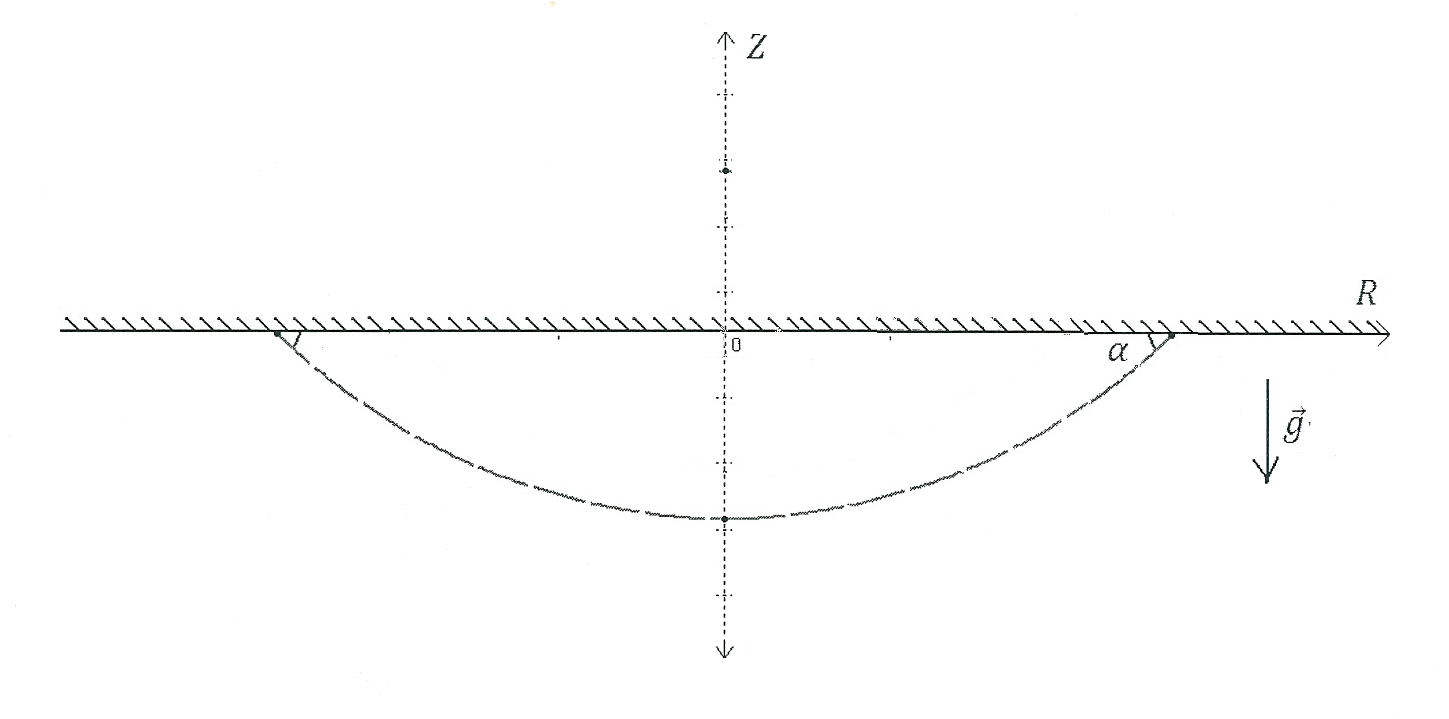

Рисунок 2 – Расположение координат

Ф = -1, если пока движение вдоль линии меридиана происходит в направлении возрастания S, жидкость остается справа, И Ф =1, если жидкость остается слева. В нашем случаем будем рассматривать Ф =1.

Также выполняется естественное условие:

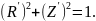(3)

Так как форма капли симметрична относительно оси OZ, достаточно получить решение для любой половины поверхности, а потом отразить решение на другую сторону. Выберем правую половину.