1.2.3. Синхронизация и координация агентов

До сих пор при параллельной композиции агентов мы не накладывали никаких ограничений на отношение порядка между событиями агентов. Однако часто мы хотим выразить, что между множествами событий про­цессов параллельно протекаемых агентов должны иметь место опреде­ленные отношения. Тогда мы говорим о координации иди синхронизации параллельных процессов. Дш этой цели наряду с уже представленной полностью независимой параллельной композицией агентов мы введем несколько позже оператор композиции, который разрешает координа­цию параллельно выполняющихся агентов.

Координация особенно необходима, чтобы при параллельно проте­кающих процессах можно было исключить конфликты.

Пример (координируемый параллельный процесс). Рукопожатие двух персон можно описать как параллельный процесс, как это показано на рис. 1.29. При этом рукопожатие есть общее действие обоих параллельно протекающих процессов, которые моделируют поведение персон А и В. Г

Пусть pi = (Ei, <i, ai) a P2 = (Е₂, <2- ct₂) - параллельно протекающие промессы. Элементы множества событий К = Ej п Е₂ называются общи­ми событиями процессов pi и р₂. Действия, которыми помечены общие события, называются синхронными. Естественно, мы требуем, чтобы для причинных порядков координирование протекающих пара-тлелышх про­цессов pi и р₂ причинные порядки на общих событиях совпадали:

<l|K х К = <2|к х К ■

Рис. 1.29. Процесс рукопожатия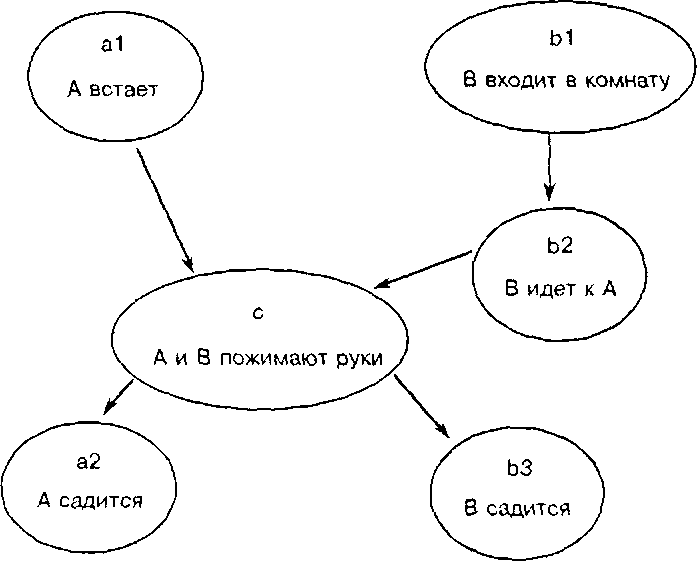

Пусть S - подмножество множества действий А. Процесс ро = (Ео, <о, ао) может быть сложен из процессов р] и р₂ тем, что мы события, помечен­ные действиями из S, установим в качестве общих событий. Тогда спра­ведливо:

ispar(po, рь Р2. S) .

Нам хотелось бы также использовать другие отличительные признаки .для охватывация соответствующих действий применительно к синхронизи­руемому множеству S, чтобы установить, какие события параллельных процессов должны быть общими. Однако сначала мы ограничимся этим простым случаем. Как будет видно позже, также и действия посылки и приема, которые принадлежат к событиям действий по коммуникации (англ. rendezvous, handshake), могут рассматриваться как действия, кото­рые являются метками общих событий обоих участвующих процессов.

Позднее, при рассмотрении языков программирования для описания параллельно функционирующих систем, мы вернемся к этим вопросам.

Ради простоты в этом разделе мы рассмотрим лишь следующий част­ный случай для установления общих событий. Множество действий А разлагается на два дизъюнктивных подмножества U и S:

• действия множества U являются асинхронно выполняемыми дейст­виями,

• действия множества S являются только синхронно выполняемыми действиями.

Введение параллельных композиций агентов, которые относительно со­бытий, помеченных определенными действиями, должны протекать син­хронно, порождает новые вопросы и проблемы. Что произойдет, если оба параллельно выполняющиеся агента настаивают на синхронном выпол­нении различных (не согласующихся друг с другом) действий? В этом слу­чае не может иметь место событие (не выполняется никакое действие), поскольку для каждой пары сшгхронных действий требовалась бы готов­ность обоих агентов. Здесь мы также говорим о тупике.

Наряду с обсуждавшейся до сих пор простой, несинхронизируемой параллельной композицией агентов мы заинтересованы и в синхронизи­руемой параллельной композиции агентов. Это может происходить, на­пример, посредством синхронной параллельной композиции ||$, nie S обозначает множество действий, которые при параллельно протекающих процессах должны выполняться синхронно.

Пример (рукопожатие). Пусть имеют место действия, как в предыдущем примере. Определим процесс рукопожатия, как он задан на рис. 1.29, с помошью агента:

(al; с; а2) ||_(с, (Ы; Ь2; с; ЬЗ) .

С гюмошыо параллельной композиции ||(_С) действие с выполняется син­хронно, а все остальные действия выполняются асинхронно. I

Точное значение синхронной параллельной композиции по отношению к ходу течения процесса задается следующими правилами:

t, —-—> г, л t₂ —-—>г₂ л ispar(p, рь р₂, S) => t, |i_s t₂ —_r, ||_s r₂,

tj —Ei—>skip л t₂ ———»skip л ispar(p,pi,p₂,S) => t, ||_st₂ —-—vskip.

Эти правила яаляются обобщением уже рассматривавшихся правил для несинхронизируемой параллельной композиции. Здесь имеет место то, что какой-либо процесс есть ход работы агента ц [|st₂, если он возникает через параллельную композицию ходов работы t] и t₂, причем в парат- лельной композиции этих процессов события, помеченные действиями из S, яаляются общими событиями. Обратим внимание, что по этому оп­ределению существуют агешы, которые отличны от skip, но тем не менее являются терминальными и тем самым не могут выполнять какого-либо процесса, кроме пустого. Говорят, что такие агенты находятся в тупике.

Пример (тупик). Агент а ; b ||_(a._b) b ; а

находится в тупике, поскольку он не может выполнять ни действия а, ни действия Ь. □

Наряду с синхронизацией процессов относительно определенных дейст­вий над общими событиями имеется дальнейшее пожелание относитель­но координации параллельно выполняющихся агентов о "взаимных ис­ключениях". Определенные последовательности действий одного areirra должны выполняться без того, чтобы параллельно имели место опреде­ленные действия другого агента, например дтя избежания конфликтов между действиями. С помощью синхронной параллельной композиции

Ч lis t₂

порождается процесс, который (при отсутствии возникновения тупиков) содержит определенные линеаризации ходов работы Ц и t₂ как частичных процессов. Возникают дальнейшие причинные отношения между собы­тиями в обоих частичных процессах - это можно ввести дтя обеспечения взаимных исключений.

■ч
	Р
	/
ы	/
X
at , \	/
\	ч
\	/
\	ч

Р

Рис. 1.30. Процесс с взаимным исключением deucmsuu Ь] и Ь2Пример (взаимное исключение через пару синхронизируемых действий). Пусть даны следующие три агента:

ti = xl :: al ; р ; Ы ; v ; xl = х2 :: а2 ; р ; Ь2 ; v ; х2 к = у :: р ; v ; у .

Предположим, что действия bj и Ь₂ могут конфликтовать между собой и поэтому не должны выполняться параллельно. Для агента

Ч II t₂

возможен ход работы, заданный с помощью следующего графа действий:

al -> р bl -> v —► al —» р —► Ы -> v —► ...

а2 -> р Ь2 —► v —> а2 —> р —> Ь2 v —► ...

Этот процесс содержит пару параллельных событий, которые помечены конфликтующими действиями bj и Ь₂. В агенте

OlIM2) ll(v.p)k

такой ход работы исключается; возможный ход работы показан на рис.

30. Обратим внимание, что каждое выполнение действий р и v агента к совпадает с одними из действий р и v или агента t_b или агента t₂, но что р и v - действия в процессах tj и t₂ не помечают каких-либо общих собы­тий.

Во всех ходах работы модифицированного агента нет больше ни од­ной пары параллельных событий, помеченных действиями Ь| и Ь₂. В но­тации сетей Петри наш пример представляется так, как показано на рис.

30. Здесь в сеть Петри введен вспомогательный вентиль с для обеспече­ния взаимных исключений.

Рис. 1.31. Сеть Петри для взаимных исключений bj и b2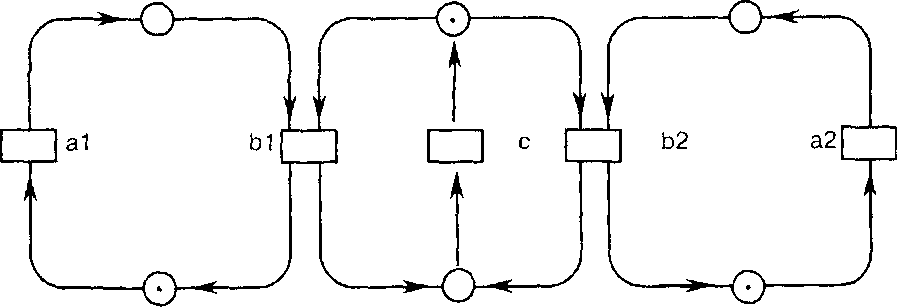

Методика обеспечения взаимных исключений, описанная в примере для агентов, может быть использована в более обших случаях. Пусть а - дей­ствие, находящееся в конфликте с самим собой, которое встречается сколь угодно часто в агентах t] и t₂. В агентах tj и t₂ заменим действие а на терм агентов

Р ; а ; V ,

причем пусть р и v - до сих пор не встречавшиеся действия в t[ или t₂. Тогда мы получим агенты tf и t₂'. Агент с::р; v; с в каждом ходе работы агента

О Г II ⁽2') lljp.vt с :: р; v; с

по мерс надобности вынуждает один из обоих агентов tf или t₂' ждать с выполнением р; a; v - до тех пор, пока агент с::р; v; с снова будет готов для события, помеченного действием р. Мы получим ходы работы вида, приведенного на рис. 1.32.

События с действием а в t'i или t"₂ в ходах работы, описанных с помо­щью агента

01* II h') 11{Р. V} С :: р; v; с,

полностью линейно упорядочены. Впрочем, при таком способе действий для обеспечения взаимных исключений возникают агенты, которые об­наруживают дополнительные возможные тупики - в случае, когда в аген­те tj или t₂ в параллельных композициях действие а должно выполняться синхронно.

Лемма (взаимное исключение). Для любого агента t, в котором действие а всегда встречается в виде р; a; v и иначе действия р и v не встречаются, справедливо, что каждый из процессов, порождаемых агентом I' вида

⁼ 0 ll(p. V} с :: р; v; с )

не содержит никакой пары параллельных событий, помеченных действи­ем а.

Доказательство. Пусть р' - процесс, порождаемый агентом t'. События, которые помечены действиями р или v, образуют последовательный под- Процесс, в котором р и v чередуются. Каждому событию е, помеченному через а, может быть однозначным образом предписано натуральное число n_v(e), соответственно п_р(е) - число событий, которые являются причиной Для е и которые помечены через v, соответственно через р. Каждому со­бытию е, помеченному через а, можно однозначно предписать помечен­ное через р событие ег_р(е), которое является причиной для е, а также помеченное через v событие er_v(e), для которого е яатяется причиной.

Ч -396с: p; v; с P

t2

Информатика. Часть III t1

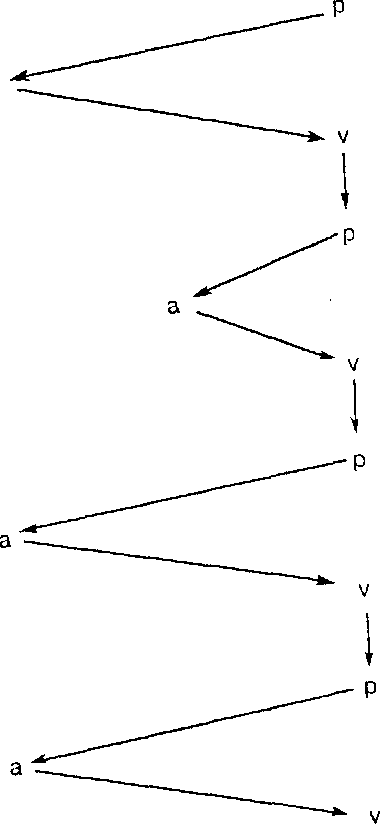
Puc. 1.32. Взаимное

исключение с помощью р- и v-действий

Индукция по числу событий показывает, что n_p(e) = п_р(ег_р(е)), n_v(e) = n_v(er_v(e)). Транзитивность отношения причинности дает, что по­меченные действием а события образуют также последовательный под­процесс. □

Обратим внимание, что благодаря обеспечению взаимного исключения путем дополнительного введения координирующих действий, надо при­нимать в расчет новые тупики. Поэтому, как правило, требуется тща­тельный анализ, чтобы исключить такие нежелательные побочные эф­фекты.

К вопросу о взаимных исключениях мы еще раз вернемся в разделе о языках программирования для описания распределенных систем.