
- •1. Процессы, коммуникация и координация в распределенных системах
- •1.1. Процессы
- •1.1.1. Структуры действий как процессы
- •1.1.2. Структурирование процессов
- •1.1.3. Последовательное представление процессов с помощью трасс
- •1.1.4. Рашуженис процесса на подпроцессы
- •1.1.5. Действия как переходы состояний
- •1,2. Описания систем через множество процессов
- •1.2.1. Сети Петри
- •1.2.2. Термы для описания процессов
- •1.2.3. Синхронизация и координация агентов
- •1.2.4. Предикаты над процессами
- •1.3. Языки программирования для описания взаимодействующих систем
- •1.3.1. Коммуникация через обмен сообщениями
- •1.3.2. Общие программные переменные
- •1.3.3. Языковые средства для параллельных ходов работы
- •1.3.4. Потоки ввода/вывода
- •2.1. Основные аспекты операционных систем
- •2.1.1. Функции операционной системы
- •2.1.2. Режимы обработки
1.2.2. Термы для описания процессов
Для моделирования поведения дискретных систем могут быть привлечены множества процессов. Такие множества допускают также описания с по мощью термов языков программирования. Это можно продемонстрировать на примере простого языка. Используемая нотация для программ, которые описывают общие процессы, базируется на нотации языка CSP ("Communicating Sequential Processes"), который разрабатывался примерно с 1976 г. Хоаром для описания взаимодействующих систем.
Мы будем использовать языковые термы, называемые агентами, для представления систем. Рассмотрим следующий БНФ-синтаксис языка агентов:
<agent> ::= skip |
<action> j
<agent> ; <agent> | <agent> or <agent>| <agent> || <agent> | <agent> id |
<agent id> :: <agent>
Будем считать, что здесь <action> обозначает некоторый наперед заданный принятый язык для описания отдельных действий, a <agent id> - тоже наперед заданное множество идентификаторов для агентов. В случае необходимости термы агентов будем заключать в скобки.
С помощью этого простого языка агентов, как и с помощью сетей Петри, могут описываться множества процессов. Эти множества снова означают ходы работ агентов. Например, агент
skip
может выполнить только пустой процесс.
Агент, который состоит только из задания действия а, в качестве ходов работ имеет множество процессов, которые обладают единственным событием, помеченным действием а. Агенг
<1 ; t2
соответствует последовательной композиции процессов, описанных агентами ti и Агент
Ч or t2
в качестве множества процессов обладает объединением множеств процессов, описанных агентами tj и t2. Агент
t 1 II г 2
описывает множество процессов, которое содержит параллельную композицию не координируемых процессов, описываемых агентами ti и t2. Форму пара_1лельной композиции, при которой агенты выполняются ко- ординированно, мы обсудим позднее.
Пусть t есть терм агента, в который свободно входит идентификатор агента х. Агент
х :: t соответствует агенту (вызову агента) х, который характеризуется рекурсивным объявлением х = t. Обратим внимание, что с помощью рекурсивно определенных агентов moot быть специфицированы бесконечные процессы.
—^CD СХ>—
'CD—^QD
Рис. 1.26. Бесконечный процесс рекурсивных агентов х::а; (Ь || х)
Пример (рекурсивно определенный агент). Следующие агенты определены рекурсивно:
светофор:: (красный; желтый; зеленый; светофор), х :: а; (Ь || х).
Первый агент соответствует агенту, определенному через рекурсивное равенство
светофор = (красный; желтый; зеленый; светофор). Соответственно для второго areirra справедтиво: х = а; (Ь || х).
Повторные подстановки правых частей равенств вместо идентификатора светофор, соответственно вместо идентификатора х, дают агенты
красный; желтый; зеленый; красный; желтый; зеленый; светофор,
и соответственно
а; (Ь || (а; (Ь || х))).
При неограниченных повторениях подстановок получаются "бесконечные" агенты
красный; желтый; зеленый; красный; желтый; зеленый; ...
и соответственно
а; (Ь || ( a; (b || ( а; (Ь || ...)...),
которые соответствуют бесконечному процессу
красный -> желтый зеленый красный ~> ...
и соответственно процессу, приведенному на рис. 1.26. □
Следующим примером мы хотим прояснить связь между сетями и агентами.
Рис.
1.27.
Представление питьевого автомата сетью
Петри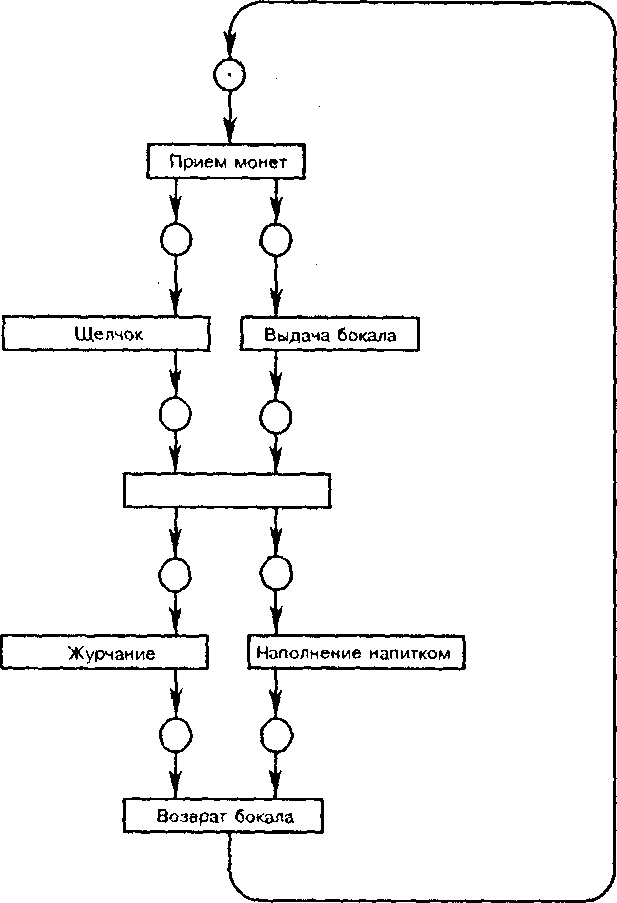
Пример (представление питьевого автомата сетью и агентами). Питьевой автомат может быть описан с помощью агентов следующим образом:
автомат:: прием_монет;
(щелчок || выдача_бокала); (журчание || наполнение_бокала_); воз врат_с вобод! ю го_бо кала; автомат.
Такой автомат может быть также представлен как сеть Петри - это пред- стаатение приведено на рис. 1.27.
Из этого примера становится ясным, что при известных обстоятельствах необходимо использовать непоименованные вспомогательные вентили, чтобы выразить поведение агента сетью Петри. G
Для каждого терма t синтаксической единицы <agent> и каждой структуры действий
Р = (Е0, <о, а)
можно аналогично конкретизациям сетей Петри установить, представляет ли структура действий р возможный ход работы агента t. Это можно сделать формально с помощью определения отношения (аналогично отношениям переходов между состояниями сети Петри)
Р
Ч > t2,
которое свидетельствует о том, что агент t, может выполнить процесс р и после этого ведет себя как агент t2.
Это отношение, которое устанавливает, какие ходы работы возможны для агентов и к каким агентам они ведут, определяется снова рекурсивно следующим образом:
(I) Каждый агент может выполнить пустой процесс. Для пустого процесса ро и любого агента t определим соответственно:
Агент а, состоящий из единственного действия а, может выполнить процесс, который содержит единственное событие, помеченное действием а. Определим:
а —-—> skip, причем р = ({е}, <j , а), а(е) = a, е - любое.
Пусть р, ро, Р[ и р2 - любые процессы. Агент tj or t2 показывает недетерминированно поведение агента ti или агента t2. Определим:
t, —t3 => t, ОГ t2 P—* t3,
t2 —> t3 => t, 0Г t2 ► t3.
Агент t2 ведет себя как агент tj и, если tj этим поведением переводится в skip, в заключение ведет себя как агент t2. Соответственно этому определим следующие два правила для последовательной композиции агентов:
t, —> t3 => tb t2 ——> t3; t2,
tj —-—> skip a t2 ———► t3 л isseq(p, pb p2) => ti; t2 —-—> t3.
Предикат isseq для характеризации последовательной композиции мы уже ввели в разд. 1.1.4.
Поведение агента Ц || t2 складывается параллельно из поведения ti и t2. Если поведение обоих агентов приводит к skip, то и поведение t] || t2 тоже приводит к skip. Другими словами, агент ti || t2 завершается, если завершается как tb так и t2. Соответственно мы определяем:
Ч —-—>П л t2 ——> г2 л ispar(p, рь р2, 0) => t, 112 —► г, | ,-2>
ti—-—► skip a t2———>-skip л ispar(p,р!,р2,0) => t|||t2—-—>skip.
Предикат ispar для харакггеризации параллельной композиции также был уже введен в разд. 1.1.4.
(4) Дтя любого процесса р определим ходы работ для рекурсивных агентов с помощью следующего правила:
t[x:: t/x] ——> t0 х:: t —> t0 .
При этом
tHi/x]
представляет агента, который получается из t путем замены всех свободных вхождений х в t на tj.
Последнее правило показывает, что рекурсивно определенные агешгы при желании можно развертывать любым способом.
Теперь через определенное выше отношение каждому агенту можно предписать множество процессов. Процесс р называется (несовершенным) ходом работы агента t0, если существует агент t! с
to ——» t, .
Снова справедливо, что множество ходов работ яатяется замкнутым относительно образования префиксов.Информатика. Часть III
Лемма (закон разложения). Если для агентов to, t2 и конечного процесса р справедливо высказывание
to ——» h>
то для каждого префикса pi с Р существует агент t[ такой, что
to—?J—*
tl и t,
Рз
> t2
с pi = р|по\ЕЬ причем пусть Ео есть множество событий процесса р, a Et - множество событий процесса pj.
Доказательство. индукцией по числу событий в pi- D
Закон разложения означает, что осуществляемые с помощью процессов переходы также могут быть разложены в следующие друг за другом переходы, причем эти последние осуществляются подпроцессами исходного процесса.
Справедливо также и обратное утверждение.
Предложение (связывание процессов). Если для агентов tb t2, t3 и процессов ро, pi справедливо высказывание
р,. Pi t, : > t2 Л t2 ► tj ,
то сулцествует процесс p2 такой, что
Доказательство, индукцией по структурам агентов. I
Агент t0 называется терминальным, если для любого агента t] высказывание
р
to ► »,
справедливо только с пустым процессом р. Таким образом, терминальный агент может осушесталять переходы только с пустым процессом, т. е. не выполняя каких-либо действий.
Процесс р называется совершенным ходом работы агента to, если для терминального агента t) справедливо:
to ——* ti,
или же процесс р является бесконечным и каждый его префикс р] с р является ходом работы.
Два агента называются эквивалентными, если они обладают одинаковыми множествами совершенных ходов работы.
К анализу агентов можно поставить такие же вопросы, какие ставятся и для сетей Петри. Впрочем, для этого концепцию сети Петри с кон- кретизациями мы заменяем концепцией агентов. Тем самым агенту соответствует при сетях пара (N, Ь), причем N представляет сеть, a b - ее конкретизацию. В случае сетей только рассматривается отношение переходов на конкретизациях, так как сеть оставляет переходы неизменными.
Пример
(свойства агента). Рассмотрим агент х
:: а ; (b
or с)
; х .
р
Дтя агента, который моделирует распределенную систему или определенный ее аспект, нас интересуют между прочим следующие вопросы:
Какими свойствами обладает множество достижимых агентов? Является ли это множество конечным?
Исключается ли для определенных действий, что будет порожден процесс, в котором оба эти действия имеют место одновременно (взаимное исключение)?
Может бы быть с помощью процесса достигнут агент (отличный от skip), для которого возможны только тривиальные переходы (тупики)?
Может ли быть достигнут агент (отличный от skip), исходя из которого больше не достижим никакой агент, в котором имеют место определенные действия (локальный тупик, отсутствующая живучесть)?
Существуют ли бесконечные процессы, в которых одно из действий никогда не встречается (справедливость)?
С примерами агентов с тупиками мы познакомимся в следующем разделе. Продемонстрируем исследование приведенных свойств на следующем
простом примере.
Рис.
1.28. Диаграмма
переходов для агента
1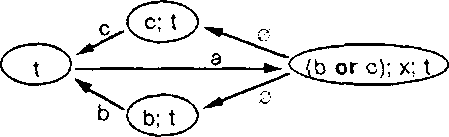
Множество агентов, достижимых от этого терма через переходы, задается с помошью следующего терма (пусть t - сокращенное обозначение терма х::а; (b ог с); х):
{t, ((b or с) ; t), (b;t), (с ; t) }.
Для агента t получаем диаграмму переходов, приведенную на рис. 1.28 (через 0 обозначен пустой процесс). Поскольку мы для агента не выдвигали предположения справедливости, для arcirra существует бесконечный процесс, в котором действие b не встречается. □
Обратим внимание, что при таком простом представлении агентов мы сознательно избегаем подробного обсуждения вопроса завершения действий и агентов. Как раз в связи со справедливостью здесь возникают сложные постановки вопросов.
