1,2. Описания систем через множество процессов

Процесс описывает возможное функционирование распределенной сис­темы. Распределенные системы обладают многими ходами работы. Абст­рактное описание динамического поведения распределенной системы может быть дано путем задания множества процессов. Существует ряд формализмов для описания систем и их ходов работ. Тремя представите­лями таких формализмов являются:

• сети Петри, графический метод описания;

• агенты, формальный язык описания;

• формулы логики предикатов для описания хода работы.

В следующем разделе мы дадим определения, которые позволяют каждо­му из описаний системы указанными выше способами предписать мно­жество процессов в качестве ходов работ.

Другие методы описания для распределенных систем и их поведения дают нам языки программирования и программы. Если программа вы­полняется на ЭВМ, то протекает некоторый процесс, который складыва­ется из множества событий, соответствующих действиям при выполне­нии программы. Программа, между прочим, описывает операционным способом также процесс. Последовательные программы описывают по­следовательные процессы. Однако для описания общих, не последова­тельных процессов языковых средств обычных, последовательных языков программирования оказывается недостаточно. Поэтому для описания па­раллельно выполняющихся систем программ, например для параллель­ной композиции, коммуникации между частями программы и синхрони­зируемого доступа к обшей памяти, применяются дополнительные язы­ковые средства.

1.2.1. Сети Петри

Одной из первых концепций, которые были предложены для описания распределенных систем и процессов, являются сети Петри, представ­ляющие собой простое графическое представление таких систем. Они были введены С. A. Petri в 1962 г. в его диссертации, посвященной опи­санию коммуникаций в автоматах.

Сеть Петри, или, точнее, сеть условий/событий, есть направленный граф, состоящий из узлов двух типов - так называемых вентилей (другие термины: переходы, барьеры. - Пер.) и ячеек (другие термины: места, площадки. - Пер.). Ребра по мере надобности ведут от вентилей к ячей­кам или от ячеек к вентилям. Ячейки загружаются логическими значе­ниями или натуральными числами. Содержимое ячеек определяет со­стояние сети. В каком-либо заданном состоянии определенные вентили (множество вентилей) головы к передаче (они могут "открываться" - пу­тем открытия такого множества вентилей изменяется загрузка сети, т. е. содержимое ее ячеек).

Рис. 1.17. Сеть Петри для задачи протводите.1ъ-потребителъ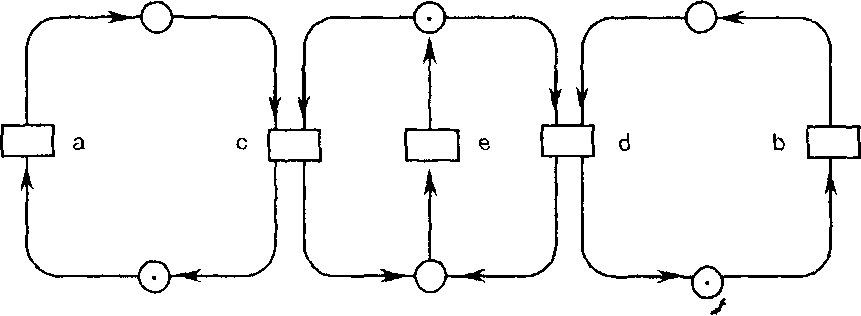

Рис. 1.18. Сеть Петри для задачи производите.1ъ-потребителъ с конфликтной загрузкой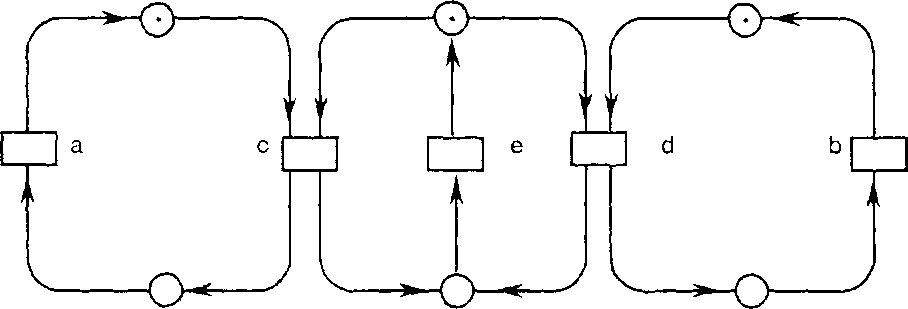

Пример (сеть условия-события). На рис. 1.17 приведена сеть Петри. Пря­моугольники обозначают вентили, а круги - ячейки. Ячейки с меткой в виде точки внутри обозначают в булевской сети ячейки, в которые за­гружено true, или 1; в остальные ячейки пусть загружено false, или 0. В сетях с ячейками, загружаемыми натуральными числами, в одной и той же ячейке может находиться несколько меток. В заданной на рис. 1.17 сети готовы к открытию ветчин а и Ь, так как все ячейки на их входя­щих ребрах загружены положительно. После того как оба эти вентиля бу­дут открыты, мы получим сеть, показанную на рис. 1.18, с указанной там загрузкой. Теперь снова готовы к передаче определенные вентили (на этот раз с и d). Впрочем, теперь может открыться вентиль с или d, но не оба сразу. 2Теперь дал им точное определение сети Петри и правил ее перехода от одной загрузки к следующей. Пусть дано множество (универсум) Т вен­тилей и множество Р ячеек (с Р n Т = 0). Сеть Петри есть тройка (То, Ро, R), такая, что справедливо

Т₀сТ вентили,

Р₀СР ячейки,

R £ (То х Р₀) и (Ро х То) отношение потока.

Мы предполагаем, что множества То и Ро конечны. Тем самым сеть Пет­ри есть бичастичный направленный граф. Граф называется бичастичным, если множество его узлов разбито на два класса и ребра могут соединять только узлы из различных классов.

Для сети Петри (То, Ро, R) каждое отображение Ь: Р₀ N,

которое ячейкам предписывает числа, означает целочисленную конкрети­зацию (занесение в ячейки конкретных чисел). Сети с целочисленными конкретизапиями называются также сетями ячейки-вентили. Часто для некоторых ячеек устанавливаются дополнительно определенные наи­большие значения ("мощность" ячейки), которые могут иметь заносимые в эти ячейки значения.

В некоторых случаях ограничиваются сетями Петри с конкретиза­пиями, пепользуюшими только значения 0 и 1, или соответственно false и true. При этом рассматриваются только конкретизации вида Ь: Р₀ В.

В таких случаях говорят о булевских сетях Петри или сетях условия- события.

Динамическое поведение сети может быть описано через процессы переключений. Вентили переключаются благодаря тому, что они извле­кают метки из всех входных ячеек и добавляют метки во все выходные ячейки. Процесс переключения может, в частности, изменить все метки в сети. Отдельные вентили готовы к передаче, если все их входные ячей­ки конкретизированы строго положительно.

Для целочисленной конкретизации b сети Петри (То, Ро, R) (непустое) подмножество К с То называется готовым к передаче, если ;пя каждой ячейки р е ро справедливо:

|{к ₆ К: (р, к) е R}| < b(p).

Множество К вентилей по этому определению для некоторой конкрети­зации готово к передаче, если в каждой ячейке р находится достаточно меток, чтобы все вентили к £ К, для которых стрелка от ячейки р ведет к вентилю к, при переключении были снабжены метками. Если для каких- то ячеек предусмотрены ограничения на помещаемые туда метки, то го­ворят об ограничении мощности. Множество К только тогда готово к пе­редаче, когда проходящие через вентили метки не превосходят соответст­вующие максимально допустимые значения. В случае булевских сетей Петри для каждой ячейки р е Ро и каждого вентиля к € К мы требуем выполнения следующего условия для готовности к передаче множества вентилей К с Т:

(р, k) е R => Ь(р) д |{к е К: (р, к) е R}| < 1

и дополнительно следующего условия бесконфликтности: для каждой ячейки р е Ро и каждого вентиля k е К должно иметь место

(к, р) е R => -Ь(р) л |{к е К: (к, р) е R}| < 1.

Это условие говорит о том, что вентиль к может открыться только тогда, когда все ячейки, к которым ведут ребра из к, помечены через false. Соо­бразно этому булевские сети Петри соответствуют целочисленным сетям Петри, в которых каждая ячейка имеет мощность 1.

В булевских сетях Петри мы дополнительно требуем выполнения следующего условия "отсутствия петель": никакой вентиль не имеет пра­ва использовать одну и ту же ячейку' как в качестве входной, так и в ка­честве выходной ячейки. Выражаясь математически, должно выполнять­ся следующее условие:

V t еТ₀, р е Р₀: -((t, р) е R л (р, t) е R).

Если бы для какого-либо вентиля t это условие не выполнялось, то такой вентиль t (при учете правила переключения для сети условие-событие) никогда не был бы готов к передаче.

Пример (сеть условие-событие). На рис. 1.19 дана сеть условие-событие. Здесь как множество вентилей {aj}, так и множество faj} готово к пере­даче, но не множество {aj, □

Для целочисленной конкретизации bo сети Петри (То, Ро, R) и готового к передаче множества К вентилей конкретизация bi называется после­дующей конкретизацией для К, если для каждой ячейки р е Ро справедли­во высказывание:

b](p) = bo(p) - |{к 6 К: (р, к) е R}| + |{к € К: (к, р) € R}|.

Конкретизация Ь[ для каждого готового к передаче множества К опреде­ляется однозначно. Для булевской конкретизации bo сети Петри (То, Ро, R) конкретизация bj называется последующей конкретизацией для гото­вого к передаче множества К, если для каждой ячейки р е Ро справедлива следующая формула:

Из определения множества, готового к передаче, тотчас же следует, что таковым является и любое подмножество этого множества. Следующая лемма показывает, что готовое к передаче множество может быть произ­вольным образом разложено в такие же подмножества и что соответст­вующие передачи могут быть осуществлены одна после другой.

Лемма (линеаризация). Пусть заданы сеть Петри и множество К венти­лей со следующим дизъюнктивным разложением:

К=К,^К₂, К,пК₂ = 0.

Тогда имеет место: если множество К готово к передаче для конкретиза­ции Ь_ц с последующей конкретизацией Ь, то имеется такая конкретиза­ция Ь[, что справедливо: Kj готово к передаче с последующей конкрети­зацией Ь_ь и К₂ готово к передаче для bj с последующей конкретизаци­ей Ь.

Доказательство. Определение готовности к передаче К влечет за собой готовность к передаче любого его подмножества К|. Для последующей конкретизации bj при К] для b₀ подмножество К₂ готово к передаче, так как К = К] К₂ было готово к передаче для bo. Поскольку К] п К₂ = 0, то сумма эффектов от К] и К₂ есть эффект К. I

Рис. 1.19. Пример для сети условие-событие

bi(p) = ((bo(p) a к € К: (p, к) € R) v 3 к e К: (к, р) е R).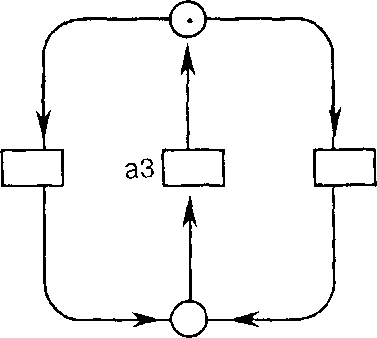

В дальнейшем для каждой сети Петри мы предпишем процессы в качест­ве хода работы этой сети. Для этих процессов в качестве множества дей­ствий будем использовать множество вентилей сети Петри. Сеть Петри обладает, как правило, большим число процессов как ходов -работы. Ис­ходя из начальной конкретизации сеть Петри порождает ход работ (процесс пробегает по сети Петри) благодаря тому, что активизируются

готовые к передаче множества вентилей и выполняются соответствующие им действия, в результате чего и осуществляется переход к последующим конкретизациям.

Для сети N = (Т₀, Ро, R) рассмотрим процесс р = (Ео, <о, ее) с марки­ровкой событий через действия:

а: Е₀ -> То ■

Для (исходной) конкретизации Ь₀ и сети Петри No = (Т₀, Р₀, R) конечная структура действий р = (Ео, <о, а) называется ходом работы сети Петри с конечной конкретизацией Ь), если р соответствует поведению сети с ис­ходной конкретизацией bo- Тогда мы пишем

b₀ ——* bj.

Это отношение между конкретизацией и процессами для заданной сети определим индуктивно следующим образом:

1. Пустой процесс всегда есть ход работы и не меняет конкретизации. Так что для пустого процесса р и любой конкретизации b справедли­во следующее отношение:

b-JU ь.

2. Пусть р = (Е₀, <о, а) - процесс с тривиальным причинным порядком, в котором рахшчные события яаляются причинно независимыми. Это значит, что для процесса р справедливо следующее высказыва­ние:

   5. е, d £ Ео: е <о d <=> е = d.

Тогда для конкретизации bo и Ь[ отношение

bo ——► Ь]

справедливо только тогда, когда все события в р помечены по- разному и потому справедлива следующая формула:

5. е, d е Ео'. е * d => а(е) * a(d),

и множество К = {а(е): е е Ео) для конкретизации Ь₀ готово к пере­даче и ведет к последующей конкретизации bj.

3. Для каждого процесса р = (Ео, <о, ао), который не удовлетворяет ус­ловиям (1) или (2), отношение

bo Ь₂

справедливо только тогда, когда для каждого непустого префикс- процесса pi = (Е_ь <i, oq) со свойством

Pl с р Л Pi * р

существует такая конкретизация Ь_ь что для процесса р₂ = РI ео\ЕI справедливо следующее высказывание:

Ь₂.

е b

Р 2

Ьо ——> bj л Ь)

/I

1\

е b

Рис. 1.20. Ходы работы сети из рис. 1.17

Это определение принимает во внимание в пункте (2) то обстоятельство, что мы понимаем вентили в сети Петри только как последовательные единицы. Параллельные события всегда маркируются различными венти­лями.

-> с -> е

Рис. 1.21. Структура действий, которая не является никаким ходом работы сети из рис. 1.17

^ио

о

а1

О

Ь2

Для каждого конечного процесса р и каждой конкретизации bo через , р

-+ b

последующая конкретизация определяется однозначно. Она получается как простои итог встречающихся действий и, соответственно, вентилей по отношению к их входным и выходным местам.

О

Ы

о

а2ПV 6

V

о.

Рис. 1.22. Сеть

ЬЗ

аЗ

Пример (ходы работы сети). Для сети из рис. 1.17 мы получаем, напри­мер, ходы работы, показанные на рис. 1.20.

Процесс р с графом действий, приведенным на рис. 1.21, не является ходом работы сети, так как для префикса pi с р (причем pi пусть содер­жит оба события, помеченные через а и Ь) достигается конкретизация, которая подпадает под условие (2), причем множество действий {с, е) не является готовым к передаче. □

Из приведенного выше определения хода работы сети получается непо­средственно следующая лемма, которая подтверждает адекватность опре­деления.

Лемма. Если для процесса р = (Ео, <о, а) н конкретизации Ь₀ и bj спра­ведливо высказывание

bo —» Ь_ь

то для каждого префикса р] процесса р с множеством событий Е[ спра­ведливо следующее высказывание: для каждого множества событий Е₂, которое является минимальным относительно <о в Ео\Е], справедливо, что множество {сс(е): е 6 Е₂} является готовым к передаче.

Доказательство. Подпроцесс в р, который состоит только из событий из Е?, для конкретизации Ь] является ходом работы. □

Пример (ходы работы сети). Пусть дана сеть, приведенная на рис. 1.22, с заданной там исходной конкретизацией. Мы получаем, например, в качестве ходов работы процессы, описанные на рис. 1.23 в виде диа­граммы действий, гак же как и их префиксы и линеаризации. П

а >Ъ, 6

/I 8

1\ 8

Как показывает следующая лемма, в сети Петри каждый префикс хода работы сам также является ходом работы.

Лемма (замкнутость относительно образования префиксов). Если процесс р есть ход работы сети N с исходной конкретизацией Ь₀, то каждый пре­фикс-процесс р| с р есть ход работы N с исходной конкретизацией Ь₀.

Доказательство. Согласно определению понятия хода работы для сети Петри процесс р есть хол работы, если любой префикс р есть ход ра­боты. ~

Структура действий р = (Ео, <о, а) называется совершенным ходом работы сети Петри N с конкретизацией bg, если справедливо Ь'дно из следующих условий:

1. Множество событий Ео бесконечно, и любой конечный префикс р есть ход работы сети N с исходной конкретизацией bo-

2. Множество событий Ео конечно, и р есть ход работы сети N для на­чальной конкретизации Ь₀ с конечной конкретизацией Ьь и для bi не существует непустого готового к передаче множества.

По этому определению сеть Петри описывает для каждой заданной ис­ходной конкретизации множества процессов, а именно ходы работы и также совершенные ходы работы сети. Приведенное выше определение ни в коей мере не принимает во внимание предположение справедливо­сти для сети Петри: в бесконечном ходе работы, смотря по обстоятельст­вам, никогда не встречается вентиль, хотя он постоянно готов к передаче (для всех конкретизации, достижимых через префиксы процесса).

Две сети с исходными коикретизациями называются эквивалентными (с точки зрения хода работы), если они имеют одинаковые множества совершенных ходов работы.

Лемма (линеаризация процессов). Если р есть ход работы сети Петри N с исходной конкретизацией Ь, то каждая линеаризация р также есть ход работы N с исходной конкретизацией Ь.

Доказательство. Каждая линеаризация, по лемме линеаризации для гото­вых к передаче множеств, может через линеаризацию достичь определен­ных готовых к переходу множеств. □

Обратное утверждение леммы не справедливо. Из множества последова­тельных ходов работы сети Петри мы не можем сделать вывод о множе­стве не последовательных ходов работы. Это показывает, что точка зре­ния интерливинга на поведение сетей Петри, при которой рассматрива­ются только последовательные ходы работ, параллельность сетей не отражает.

Бесконечный ход работы р = (Ео, <о, а) сети Петри N с исходной конкретизацией b называется несправедливым по отношению вентиля а, если выполняются оба следующих условия:

1. Множество {е е Ео: а(е) = а} событий, помеченных действием а, ко­нечно.

2. Множество конечных префиксных процессов р) с р, причем Pi = (Еь <ь а,) с

{е е Ео : а(е) = a} = {е е Е] : а](е) = а} и

р

Ь₀ ► ь_ь

причем вентиль а в Ь) готов к передаче, является бесконечным.

В несправедливом по отношению действия а бесконечном ходе работы сети Петри вентиль а встречается лишь конечное число раз, хотя он бес­конечно часто готов к передаче. Вообще, ход работы называется справед­ливым, если он не является несправедливым относительно никаких вен­тилей.

Описанное здесь понятие справедливости является лишь одним из вариантов среди многих понятии подобного рода, однако мы не хотим дальше углубляться в их различия.

Лемма (замкнутость множеств хода работ селей относительно бесконеч­ных префиксов). Если р - бесконечный процесс и ход работы сети N для исходной конкретизации Ь₀, то каждый бесконечный префикс р] с р есть бесконечный ход работы сети N для исходной конкретизации bo.

Доказательство. Каждый конечный префикс р₂ с pi вследствие транзи­тивности q также является префиксом р и поэтому также является ходом работы N для исходной конкретизации bo- -

Лемма показывает, что при определении хода работы сетей мы не при­влекали предположения справедливости.

Для заданной сети и заданной исходной конкретизации bo конкрети­зация Ь| называется достижимой, если существует такой процесс р, что

bo —> Ь,.

Вообще сеть Петри обладает большим числом ходов работы. При порож­дении ходов работы для сети остаются известные степени свободы ("возможности выбора") относительно того, какие вентили должны включаться в качестве очередных. Порожденный ход работы есть резуль­тат сети Петри, ее исходной конкретизации и решений выбора. При воз­можностях выбора в ходе работы системы мы говорим также о недетер­минированности.

Можно различать два вида недетерминированности для выбора ходов работы в сетях Петри:

(1) Вентили находятся в конфликте (они имеют обшие входные или вы­ходные ячейки, которые маркированы так, что открыться может только подмножество множества вентилей).

(2) Порядок на событиях может быть выбран путем произвольной ли­неаризации.

Для заданной сети Петри, которая моделирует поведение распределенной системы или ее определенных аспектов, нас часто интересует вопрос, ка­кие из следующих свойств выявляет сеть с определенной начальной кон­кретизацией:

1. Какие свойства имеют достижимые конкретизации? Является ли множество этих конкретизации конечным?

2. Исключено ли для определенных вентилей, что достигается кон­кретизация, в которой эти вентили одновременно готовы к передаче ("взаимное исключение")?

3. Может ли достигаться такая конкретизация, при которой больше никакие вентили не являются готовыми к передаче (тупик, англ. deadlock)?

4. Может ли достигаться конкретизация, исходя из которой больше недостижима конкретизация, при которой определенные вентили готовы к передаче (локальный тупик, отсутствие живучести, англ. livelock)?

5. Существуют ли (справедливые или несправедливые) бесконечные ходы работы, в которых некоторые из вентилей никогда не используются (англ. starvation)?

^b о

^а CJ

о^—^J

Рис. 1.24. Сеть Петри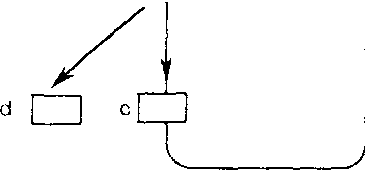

Продемонстрируем исследование введенных свойств на простом примере.

Пример (свойства ссти). Рассмотрим приведению на рис. 1.24 целочис­ленную сеть с указанной там конкретизацией. Каждая конкретизация се­ти соответствует паре целых чисел. Начальная конкретизация есть (1, 0). Множество достижимых конкретизации задается через

{(1,0), (0, 1), (0, 0)}.

Мы получаем диаграмму переходов для достижимых конкретизации, представленную на рис. 1.25.

(0, 0)

Рис. 1.25. Диаграмма переходов состояний для сети Петри из рис. 1.24

Может быть, между прочим, достигнута конкретизация (0, 0), которая представляет собой тупик. Существует бесконечный ход работы для сети, в котором не используется вентиль а, и бесконечный процесс, в котором не используется вентиль Ь.

Для сети N и начальной конкретизации b множество достижимых конкретизации можно понимать как множество состояний, для которых вентили по правилам переключений могут истолковываться как дейст­вия. Возникает автомат состояний. Тем самым сети Петри определяют автоматы состояний. При переходе от сети к соответствующим автоматам состояний не входит, однако, рассмотрение параллельности.

Наряду с уже упомянутыми имеется изобилие дальнейших важных свойств сетей и методик для их анализа. Дтя знакомства с этими вопро­сами следует обратиться к прилагаемому списку литературы. Исчерпы­вающий обзор содержит, например [Rcisig 86].