1.1.4. Рашуженис процесса на подпроцессы

В практических приложениях информатики встречаются распределенные системы большой количественной и качественной сложности. Для струк­турированного обращения с ними решающее значение имеет их разложе­ние на частичные компоненты. Поэтому обратимся теперь к вопросу о том, может ли процесс ро быть рахтожен параллельным или последова­тельным образом в подпроцессы р) и р₂, или наоборот - можно ли про­цесс ро представлять себе образованным из подпроцессов. Такая форма разложения позволит сделать достаточно простое сопоставление между

множествами процессов для описания системы. Пусть заданы следующие процессы:

Ро = (Ео, <о, «о), Pi = (Еь <ь а0,

Р2 ⁼ (Е2, <2ь а₂)-

Мы скажем, что процесс ро можно понимать как последовательную ком­позицию процессов pi и р₂ или, наоборот, что процесс ро допускает по­следовательное разложение в процессы р! и Р2, если процесс ро можно получить с помощью процессов р] и р2, выполняемых последовательно один за другим. Для такого отношения между тремя процессами будем писать предикат

isseq(p₀, рь р₂).

Математически этот предикат над процессами определяется следующим уравнением:

isseq(p₀, рь Р2) =def (Ео = Ei и Е₂) л (Ei о Е₂ = 0 ) л (po|ei= Pi) л (ро|е2= рг) а v е е Ej, d € е₂: е <о d.

Не каждый процесс, как это показывает приводимый ниже пример, мо­жет быть разложен на непустые последовательные процессы.

^ ^ ^е

а d о

а— ^

Рис. 1.10. Процесс без нетривиа.гьного последовательного разложения

Рис. 1.8. Граф действий процесса р

Рис. 1.9. Разложение р в подпроцессы b ** с f

Пример (последовательное разложение процессов). Процесс р, заданный на рис. 1.8, может быть разложен, как это показано на рис. 1.9, последо­вательно на два процесса. Для процесса, заданного на рис. 1.10, не суще­ствует никакого нетривиального последовательного разложения. При этом рахюжение мы называем тривиальным, если один из двух подпро­цессов, возникающих с помощью разложения, является пустым. и

Скажем, что процесс ро можно понимать как параллельную композицию процессов pi и Р2 с общими действиями из S с А или что процесс ро до­пускает разложение в параллельные процессы pi и Р2 с общими дейст­виями из S с А, если процесс р₀ получается путем параллельного выпол­нения процессов pi и р₂, причем множество событий в точности совпа­дает с событиями, помеченными действиями из S. Для этого отношения между тремя процессами будем писать предикат

ispar(p₀, Рь Р2, S).

Математически этот предикат определяется следующим уравнением:

ispar(p₀, Рь р₂, S) =_d(;f (Eq = Ej и Е₂) л

(Е, пЕ_г = (ее Е₀: а₀(е) е S}) л («о|П1 = «0 ^л («о1г:2 ^{= а}2) ^л

(<0 = (<1 и <,)*).

Здесь (<i и <2)* обозначает рефлексивно-транзитивное замыкание отно­шений <i и <2-

Частный случай параллельной композиции получается для S = 0. Тогда в возникающем процессе ро события из различных процессов р] и Р2 яатяются причинно-независимыми.

Пример (параллельное рахюжение процессов).

(1) Процесс, показанный на рис. 1.11 с помощью диаграммы действий, может быть рахтожен в два параллельных процесса, заданных на рис. 1.12, причем пусть множество общих событий помечено действиями из S = {с, е}.

Рис. 1.11. Процесс ро

а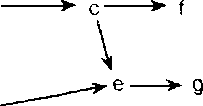

b

V

Рис. 1.12. Лараи&1ьное разложение процесса ро

(2) Два процесса, заданные на рис. 1.13, при их параллельной компози­ции с общими событиями, помеченными действиями из {b, d}, дают про­цесс, показанный на рис. 1.14.

В обоих примерах необходимо образование транзитивного замыкания. О

▼

d

f

Рис. 1.13. Процессы pj и рх

/ N

I ^d

\

f

Рис. 1.14. Паралле.гьная композиция из pi и Р2

g

\

Обратим внимание, что для граничного случая S = 0 при параллельно! композиции для процесса р₀ мы получаем тривиальное параллельное со четакие процессов Pi и (причем множества событий должны быть раз

дельны). Для граничного случая S = А получится процесс с множеством событий, получаемым путем объединения множеств событий (которые должны быть идентичны) обоих процессов, и с причинным порядком, которое образуется через транзитивное замыкание причинных порядков обоих процессов.

В противоположность последовательному разложению каждый не­тривиальный процесс допускает нетривиальное параллельное разложе­ние. Мы обычно заинтересованы в разложениях, при которых множество общих событий было бы возможно меньше, и тем самым независимая параллельность была бы возможно больше.