1.1.2. Структурирование процессов

В случае сложных конечных или же бесконечных процессов рассмотре­ние нестр^тсгурированного множества всех событий и связанных с ними действий быстро становится труднообозримым. Часто какой-либо про­цесс складывается из ряда частичных процессов (подпроцессов) или по меньшей мере он может быть так описан. Такого рода процесс можно анализировать путем его умелого разложения на подпроцессы и их ана­лиза.

Пусть р, = (Е[, <i, cq) и р2 = (Е2, <2, 0-2) ' процессы. Если имеет ме­сто следующее отношение между Pi и Р2:

Е, с Е₂,

«2|_Г1 = «1 ,

Е1 ⁼-1 '

то р] называется частичным процессом (подпроцессом) Р2- Мы обозначаем процесс pi также через p^i (и говорим: "р₂ ограниченный на множестве событий Е]"). Если дополнительно справедлива формула

V е е E2.de Ei: е <2 d => е е Е[ ,

то процесс pi называется началом или префиксом процесса Р2, и тогда пишут

Pi с р₂.

Префикс-отношение моделирует предшествование процесса во времени. Каждый префикс процесса может пониматься как описание начального отрезка поведения процесса.

Лемма. Префикс-отношение есть частичный порядок на множестве про­цессов.

Доказательство. Рефлексивность отношения тривиальна. Антисимметрия

показывается следующим образом. Если имеет место

Pi SP2 л р₂ ерь

го справедливо Е| = Ег н по данному выше определению <j = <2 и

«1 = С£2-

Транзитивность показывается так. Если имеет место Pi СР2 л р₂ срз,

то через транзитивность отношения подмножеств Ei с Е3 и по тому же

определению также

«уд = <*1 .

^3|Г.1 Е! ⁼

Из

5. с, d s Е2: е <2 d л d е Ej => е е Е;,

и

5. е, d е Е₃: е <3 d л d € Е2 => е е Е2,

и

Ve.de Е₂: е <3 d => е <₂ d

тотчас следует

5. с, d е Е3: е <3 d л d е Ei => е е Ej, 5

Конечно-вложенные структуры действий по отношению префикса имеют особое свойство: множество конечных префиксов (префикс-процессы с конечным множеством действий) однозначно характеризует процесс. Это особенно важно для описания бесконечных процессов.

Лемма (характеризация процессов через конечные аппроксимации). Для каждого конечно-вложенного процесса pi = (Е1, <1, оц) справедливо: множество его конечных префикс-процессов М = {р: р с pi, р конечен}

определяет процесс pi однозначно. В частности, справедливо Pi = sup М

Доказательство. Несомненно, процесс pi есть верхняя граница М относи­тельно префикс-порядка. Пусть Р2 = (Е2, <2, а₂) тоже верхняя фаница М. Тогда справедливо

Е( С Е2, так как Е> = ^J {Е₀ : (Е₀, <о, ао) е М}. Поскольку' <( и «1 на Ej совпадают с <2 и aj, справедливо также р[ с Р2-0

Эта лемма позволяет изучать и анализировать бесконечные, конечно- вложенные процессы путем изучения и анализа их конечных префиксов. Методы проведения доказательств для бесконечных процессов и характе- ризапин таких процессов будут обсуждаться в конце этой главы.

Подпроцессы возникают из заданного процесса путем затенения оп­ределенных событий, например всех событий, которые помечены дейст­виями из заданного множества. Такие подпроцессы, состоящие из семей­ства связанных друг с другом событий, называются транзакциями.

Пример (последовательные подпроцессы процесса). На рис. 1.3 с помо­щью диаграммы событий описывается процесс р и его подпроцесс.

Процесс р а Ь

Подпроцесс р|,_{а с е} ас d

ч /

е

с i

е

f I

9

✓ Ч

⁰

Рис. 1.3. Процесс и подпроцесс Заданные в табл. 1.4 действия можно связать с наступающими событиями.

Событие	Действие
а	х входит в здание
b	у входит в здание
с	х входит в лифт
d	у входит в лифт
е	Лифт идет вверх с х и у
Г	Лифг достигает 2-го этажа
g	х выходит из лифта
h	Лифт достигает 3-го этажа
i	у выходит из лифта

Таблица 1.4. События и действия процесса

Заданный подпроцесс содержит все события, которые связаны с дейст­виями липа х. □

Наряду со структурированием заданного процесса р в частичные процес­сы нас интересует и возможность изучения таких процессов с аналогич­ным множеством событий, которые отличаются от р обогащением при­чинного порядка путем вставления дополнительных пар в частичный по­рядок. В этом случае мы будем говорить о линеаризации процесса (преобразовании его в линейный, т. е. последовательный).

Процесс pi = (Еь <1, ос 1) называется линеаризацией процесса P2 = = (Ез, <2, «г)> если справедливо:

1. Е, = Е₂,

2. V с, d е Е,: е <₂ d е <, d,

3. cq = а₂ .

Если Р) - последовательный процесс, то линеаризация называется совер­шенной. Т. к. нас интересуют не сами множества событий, которые явля­ются лишь вспомогательными математическими средствами, мы говорим при ослаблении условия (1) также о линеаризации, если существует би­ективное отображение у между множествами событий Е[ и Е₂, так что об­разы биективного отображения снабжены теми же действиями, что и их прообразы. Дополнительно условие (2) модифицируется следующим образом:

(2') V е, d е Е,: v(e) <₂ 7(d) => е <, d .

Последовательный наблюдатель процесса - это наблюдатель, который удерживает события процесса и соответствующие действия в последова­тельном протоколе функционирования. Параллельные действия при этом приводятся в случайном порядке. Результат наблюдения есть последова­тельный процесс, который соответствует случайно выбранной линеари­зации. Если мы, имея дело с процессами, исходим из последовательных наблюдателен, то получаем последовательные процессы как наблюдения. При преобразовании частичного порядка к линейному порядку говорят о топологической сортировке.

Если над каким-либо не последовательным процессом существует ряд наблюдений и все они представляют совершенные линеаризации процесса, то из этих наблюдений можно частично реконструировать процесс. Если нам известно множество всех линеаризации, то процесс допускает однозначную реконструкцию.

Предложение. Каждая конечно-вложенная структура действий Ри = (Ео, <о, и) однозначно определяется множеством ее совершенных линеаризации.

Доказательство. Пусть для процесса ро задано множество совершенных линеаризаций. Множество событий и порядок действий тривиально за­даются множеством совершенных линеаризаций. Для событий е, d спра­ведливо

■ е <₀ d,

если во всех линеаризациях р] = (Eg, <1, а) процесса ро имеет место е <i d.

Если справедливо -.(е <о d), то имеется линеаризация

(Е₀, <ь а) с d <i е. □

Выполнение профаммы на ЭВМ тоже может быть представлено в виде процесса. Определенные операторы (действия) программы распадаются при их выполнении машиной на ряд отдельных действий. Эту ситуацию математически можно охватить с помощью понятия "детализация".

Процесс р] = (Ej, <i, а]) называется детализацией (уточнением) про­цесса ро = (Ео, <о, «о), если существует отображение

у: Е1 —> Ео,

такое, что справедливо следующее высказывание:

Vc.dE Е,: у(е) * y(d) => (е <, d о у(е) <₀ y(d)).

Отображение у, как правило, различным событиям в pi предписывает од­но и то же событие в ро- В соответствии с этим одно событие может быть детализировано через множество событии, которые образуют частичный процесс в р[. Тем самым для каждого события е е Ец множество М {d е Ej: у (d) = е} определяет частичный процесс ро!м-

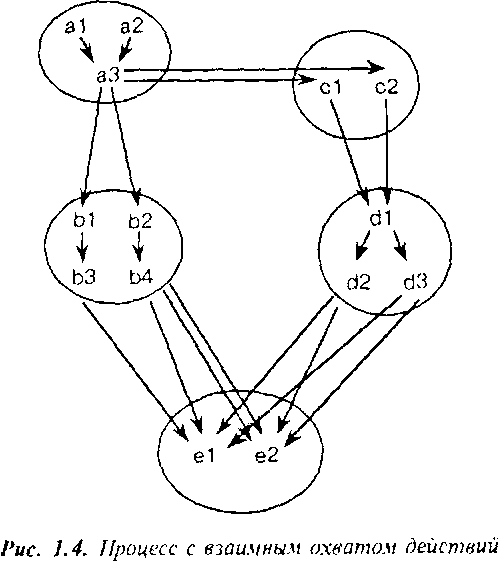
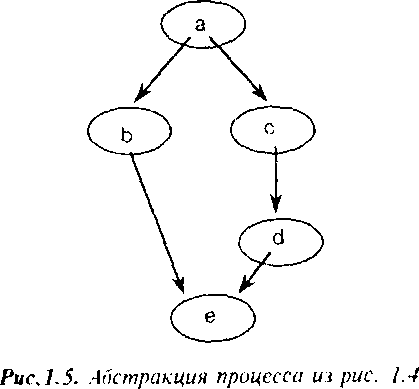
Пример (детализация процесса). На рис. 1.4 предста&лена детализация процесса, заданного на рис. 1.5. □

Событие а процесса из рис. 1.5 детатизируется, как это изображено на рис. 1.4, в три события а 1, а2 и аЗ. Аналогичным образом детализируются и остальные события. Общая структура процесса из рис. 1.5 сохраняется при детализации.

Адекватная пошаговая детализация процессов является одной из важнейших методик проектирования при создании сложных распреде­ленных систем.