1.1. Процессы

В этом разделе понятие "процесс" охватывается математически. Для этого введем понятие структуры действий. Так получаемое понятие про­цесса служит для математического моделирования любого не непрерыв­ного ("дискретного") действия распределенной системы, будь то процес­сы в ЭВМ или иного рода технические или производственные процессы, которые складываются из отдельных действий, между которыми сущест­вуют причинно-следственные отношения.

Параллельные процессы принадлежат к общим явлениям нашей по­вседневной жизни. Впрочем, у нас есть лишь интуитивное понимание параллельных процессов. Точное описание какого-либо интуитивно яс­ного параллельного течения, как, например, телефонные разговоры, об­служивание питьевых автоматов или ведение монтажа зданий, часто го­товит для нас большие трудности¹. Добавим к тому же, что язык и пись­менность, как наши наиболее употребительные формы описания, являются существенно последовательными и потом)' не могут непо­средственно представлять параллельные процессы.

Поскольку в дальнейшем мы хотим изучать как раз феномен парал­лелизма (одновременного протекания) при выполнении программ, мы введем "непоследовательную'' математическую структуру, предназначен­ную для представления параллельных процессов.

1.1.1. Структуры действий как процессы

Начнем с примера систем параллельного действия. Рассмотрим дорогу с несколькими рядами движения, пешеходным переходом и светофором. Ход событий, развертывающихся в определенный интервал времени на дороге и переходе, представляет собой параллельный ход процессов. В этом процессе фигурируют такие действия, как:

• пешеход нажимает кнопку на сфетофоре;

• светофор для машин переключается с зеленого на желтый свет;

• машина останавливается перед светофором в i-м ряду;

• светофор для машин переключается с желтого на красный свет;

• светофор для перехода переключается с красного на зеленый свет;

• пешеход пересекает дорогу.

Конечно, мы ожидаем и знаем, что в каждой ситуации, в каждом про­цессе, которые могут иметь место на дороге, между определенными из этих наблюдаемых действий возникает внутренняя причинно- следственная связь. Так, светофор для пешехода только тогда переключа­ется на зеленый свет, когда светофор для машин показывает красный свет. Светофор переключается только тогда, когда до этого будет нажата соответствующая кнопка.

Эти действия отчасти происходят одновременно. Например, многие пешеходы могут одновременно пересекать дорог)'. Конечно, и машины также могут по параллельным рядам одновременно ехать через пешеход­ный переход. Существуют, однако, ограничения на одновременное со­вершение действий. Имеются хорошо известное требование безопасно­сти: пешеходы и машины никогда не могут одновременно получать зеле­ный свет. Другими словами, светофор для пешеходов может показывать зеленый свет только тогда, когда он для машин переключен на красный свет, и наоборот.

Как могло бы выглядеть описание процесса, который протекает в оп­ределенный интервал времени на пешеходном переходе? Конечно, опре­деленные из перечисленных выше действий могут иметь место много­кратно. Поэтому важно делать различие между действием как таковым (например, "кнопка нажимается") и индивидуальным совершением ("воплощением") действия (наличие действия). При каждом воплощении действия говорят о событии. Действие распределенной системы в соот­ветствии с этим состоит из множества событий, причем каждому собы­тию предписано действие. Различным событиям могут быть предписаны одни гг те же действия. Это приводит к следующей картине математиче­ском модели для процесса.

Пусть задано множество (универсум) Е событий (англ. events), мно­жество А действий (англ. actions). Тройка р = (Ео, <о> ^а) называется структурой действия или также процессом, если справедливы следующие высказывания:

Ео S Е,

<о есть частичный порядок на;г Ео,

а: Ео —> А.

Ео называется множеством событий, <о есть отношение причина- следствие, и а - обозначение действия процесса р. Отображение а каж­дому событию предписывает действие. В это определение структуры дей­ствия сознательно включается также пустой процесс - он предстаатяется структурой действия, которая содержит пустое множество событий.

Указание (определение частичного порядка). Для заданного множества М частичный порядок <о есть (двухместное) отношение, т. е. подмножество из М х М, которое является рефлексивным, транзитивным и антисим­метричным. ~

Пример (процесс на пешеходном переходе). Рассмотрим процесс с 14 со­бытиями. В табл. 1.1 перечислены эти события и предписанные им дей­ствия.

Событие	Действие
el	Нажимается кнопка
е2	Светофор ятя машин переключается на же.ггый
еЗ	Светофор хтя машин переключается на красный
е4	Машина останавливается в ряде 1
с 5	Светофор для пешеходов переключается на зеленый
еб	Машина останавливается в ряде 2
с7	Пешеход пересекает переход
е8	Машина останавливается в ряде 3
е9	Светофор для пешеходов переключается на красный
с 10	Светофор для машин переключается на красный и
	же.ггый
ell	Светофор для машин переключается на зеленый
е 12	Машина едет в ряде 1
е 13	Машина едет в ряде 2
еН	Машина едет в ряде 3

Таблица 1.1. Пример событий и действий на пешеходном переходе со светофором

При этом примем следующие причинно-следственные отношения между событиями:

е 1 < е2, е2 < еЗ, еЗ < е4, еЗ < е5, еЗ < сб, е5 < е7, еЗ < eS, е5 < е9, е9 <с10, с!0< ell,

ell < е 12, el 1 < е13, ell < el4, e4 < с 12, еб < e 13, eS < el4 .

Эти отношения порождают (через формирование рефлексивного транзи­тивного замыкания) частичный порядок, который описывает причинно- следственную связь между событиями. Обратим внимание, что здесь, на­пример, событие е 12 имеет место только после того, как имели место со­бытия е4 и ell. 1

Конечные процессы допускают наглядное представление с помощью на­правленного, ациклического графа с помеченными вершинами. Вершины представляют события и помечены действиями (сравнить с этим приве­денное ниже определение направленного графа).

Пример (процесс на пешеходном переходе в графическом представле­нии). Графически приведенный выше пример процесса на переходе со светофором может быть описан с помощью структуры действий, пока­занной на рис. 1.1. □

е1—»- е2 -

Рис. 1.1. Процесс в графическом описании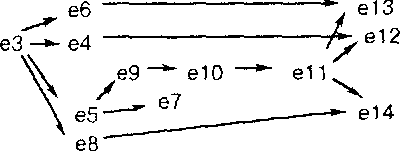

Указание (определение направленного графа). Направленный граф над множеством вершин М задастся с помощью двухместного отношения R над М. R есть подмножество М х N1. R называется также множеством ре­бер.

Пусть А - множество меток. Если для графа задано отображение а : М —» А,

то граф называется графом с помеченными вершинами. Если задано ото­бражение

у : R-» А,

то граф называется графом с помеченными ребрами. □

Наглядно графы могут быть изображены в виде диаграмм со стрелками, как на рис. 1.1. Это представление графов, естественно, возможно только при конечном множестве вершин. При графическом представлении в ви­де диаграмм со стрелками можно отказаться от явного указания множе­ства вершин, поскольку они однозначно характеризуются точками в ди­аграмме.

Пример (посадка четырех персон в автомашину с двумя дверцами). Про­цесс посадки в машину можно графически представить в виде диаграм­мы, приведенной на рис. 1.2.

Упорядочение событий для действий в этом случае устанавливается табл. 1.2. □

Часто используются диаграммы специального вида, в которых события явно не фигурируют, а задаются только действия, которыми помечаются события. В этом случае говорят о диаграммах действий.

ткштт

Событие	Действие
А	Открывается центральный запор машины
В	Открывается левая дверь, садится 1-й пассажир (через
	левую дверь вглубь машины)
С	Открывается правая дверь
D	Через правую дверь садится 2-й пассажир вглубь ма­
	шины
Е	Садится водитель и закрывает дверь
F	Садится 3-й пассажир рядом с водителем и закрывает
	дверь
G	Машина трогается

Таблица 1.2. Пример событий и действий процесса посадки в автомашину

Теперь мы вернемся к основным понятиям, которые имеют особенное значение в связи с параллельными процессами. Для процесса

р = (Но, <о, а)

назовем лва события е_ь е? е Ео пара.иельными (англ. concurrent), если они в процессе р не находятся в причинно-следственном отношении, или, выражаясь математически, если справедливо высказывание

<0 ^е2 VC] <0 С[) .

Параллельные события независимы яруг от друга и могут иметь место одновременно или в любой последовательности.

А

G

Рис. 1.2. Процесс посадки в автомашин)-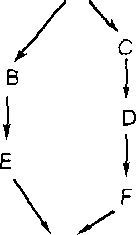

В одном процессе каждое событие имеет однозначную идентифика­цию ("X входит 07.05.84 г. в 10:10 в аудиторию"); действие же может иметь место неоднократно (X может входить в аудиторию многократно). Соответственно этому в одном процессе различным событиям может быть предписано одно и то же действие.

(Шутливый) вопрос из интеллектуального теста мог бы гласить: ''Как часто число 1 можно вычитать из числа 20?". Ответ: "Однажды" - прави­лен, если иметь в виду действие, а ответ: "Сколь угодно часто" - прави­лен, если имеется в виду событие.

Процесс р = (Eg, <о, а) называется последовательным, если не возни­кает ни одной пары параллельных событий или, выражаясь математиче­ски, если причинно-следственное отношение <о представляет линейный порядок.

Указание (определение линейного порядка). Линейный порядок <о есть частичный порядок, в котором для любых элементов е, d всегда справед­ливо е <о d или d <о е. и

Выполнение программы также может трактоваться как процесс в смысле наших структур действий. Последовательные программы порождают по­ел е до вате." I ьны е п ро це сс ы.

Пример (ханойские башни для трех шайб). В части II "Введения" в по­следней главе описана задача о ханойских башнях. Программа, которая управляет перемещениями шайб в процессе решения этой задачи, вы­полняет действия вида

ⁿ i

а >Ъ,

которые должны представлять перемещение шайбы пеана Ь.

Табл. 1.3 описывает последовательность ходов (т. е. процесс) для слу­чая трех шайб.

Событие	Действие
el	а —>Ь
е2	а —-■■-—>с
еЗ	, 1 b >с
е4	а - -J—b
еэ	L с >а
еб	с —- >Ь
е7	1 . а ->Ь

Таблица 1.3. Пример перемещения ханойских башен

Действие а -— - -->Ь в этом процессе встречается дважды.

Процесс (Ео, <о, ^а) называется конечным, если его множество собы­тий Ео является конечным множеством. В связи с тем, что в принципе имеются неограниченно долго работающие системы, например операци­онные системы ЭВМ, нас интересуют также и бесконечные процессы. Бесконечные процессы обладают бесконечным множеством событий.

Для любого частичного порядка < на заданном множестве М элемент El £ Е называется непосредственно следующим за элементом ед е Е, если для всех элементов с е Е справедливо высказывание

eo<e<ei=>(e = e[ve = eo).

Частичные порядки на конечных множествах однозначно характеризуют­ся множеством элементов, непосредственно следующих за каждым эле­ментом. Дтя частичного порядка на бесконечном множестве это не спра­ведливо. Для бесконечного процесса (Ео, <о, а) множество непосредст­венно следующих событий за каким-либо событием не может однозначно охарактеризовать частичный порядок.

Пример (нсдискретный частичный порядок). Возьмем множество рацио­нальных чисел в качестве множества событий и рассмотрим обычный (линейный) порядок. Здесь никакое число не имеет непосредственно следующего за ним числа. [Г

В структурах действий, которые соответствуют реальным процессам, вряд ли встречаются такие недискретные причинно-следственные упорядоче­ния. Поэтому в дальнейшем мы ограничимся такими процессами, кото­рые обладают дискретным причинно-следственным упорядочением. В частности, будем требовать, чтобы в каждом процессе (Ео, <о, а) для каждого события е е Eq множество причинно-следственных предшест­венников

{d е Е₀: d <₀ е}

было конечным. Структуру действий с этим свойством будем называть также конечно-вложенной. Тогда

{d е Е₀: d <о е},

так как не существует бесконечно нарастающих цепочек событий. Час­тичный порядок может быть охарактеризован тем, что для каждого собы­тия определяется множество непосредственно следующих за ним собы­тий (его последователей).

Существуют самые разные возможности для толкования частичного Порядка событий процесса. Отношение

е <₀d

ДЛЯ событий е, d е Ео шггуитивно означает следующее: справедливо е = d Или событие е является причиной для события d. Эта причинно-следст­венная связь позволяет сделать вывод, что событие е должно быть завер­шено, прежде чем может иметь место событие d. Таким образом, отно­шение причина-следствие включает временное отношение. Обратное же tie имеет места: временное отношение между событиями ничего не гово­рит о причинности. Если не справедливо ни причинное отношение е <о d> ни d <о ^е> ^то ° временном отношении событий ничего сказать нельзя.

Впрочем, часто нам хотелось бы порядок на событиях понимать не только как причинно-следственный, но и как временной. Если каждому событию предписать интервал на оси времени, то получается следующая возможность понимания частичного порядка событий:

х <о У означает "х кончается до того, как начинается у". Если допол­нительно рассматривать временную длительность событий, то событию е можно предписать время начала i(e) и время конца v(e) этого события. Получаются следующие три возможности временных расположений для событий е и d:

1. е начинается до начала d: i(e) < i(d),

2. е кончается до окончания d: v(e) < v(d),

3. е кончается до начала d: v(e) < i(d).

В наших структурах действий мы рассматриваем события, которые на оси времени имеют форму точек, т. е. соответствуют одноэлементному вре­менному интервалу. Тем самым мы моделируем только случай (3): для двух (различных) событии end справедливо v(c) < i(d), если е <о d. Если бы мы в нашем моделировании захотели явно учитывать случаи (1) и (2), мы могли бы это осуществить путем расщепления соответствующего со­бытия е на два события е₍ (е начинается) и е₂ (е кончается). В дальней­шем частичный порядок мы будем интерпретировать только как причин­ный, но не временной.

Пример (временной порядок событий). Множество событий с действия­ми "лифт достигает i-й этаж в х-й раз" последовательно упорядочено от­носительно временного порядка. □

В процессах, которые мы используем в качестве модели функционирова­ния систем, мы часто находим рахшчные поводы для причинно- следственных отношений е <о d между событиями е и d.-Мы различаем порознь:

• чисто причинные отношения (событие е есть причина появления со­бытия d),

• временные отношения (событие е кончается до начала события d),

• системные ограничения (событие е не имеет права возникать парал­лельно событию d).

Примером для третьей интерпретации является взаимное исключение пересечения дороги пешеходом и пересечение пешеходного перехода машиной. События, которые помечены действиями и которые не могут иметь место параллельно, не обязательно должны находиться в "чисто" причинной связи. Тем не менее они не должны возникать как парал­лельные события. Поэтому эти события в ходе функционирования сис­темы постоянно находятся в причинном отношении. Только тогда, когда ранее возникшее событие будет закончено, может иметь место второе со­бытие. Примеры таких ситуаций, специфичные для информатики, будут скоро рассмотрены.