
- •1. Процессы, коммуникация и координация в распределенных системах
- •1.1. Процессы
- •1.1.1. Структуры действий как процессы
- •1.1.2. Структурирование процессов
- •1.1.3. Последовательное представление процессов с помощью трасс
- •1.1.4. Рашуженис процесса на подпроцессы
- •1.1.5. Действия как переходы состояний
- •1,2. Описания систем через множество процессов
- •1.2.1. Сети Петри
- •1.2.2. Термы для описания процессов
- •1.2.3. Синхронизация и координация агентов
- •1.2.4. Предикаты над процессами
- •1.3. Языки программирования для описания взаимодействующих систем
- •1.3.1. Коммуникация через обмен сообщениями
- •1.3.2. Общие программные переменные
- •1.3.3. Языковые средства для параллельных ходов работы
- •1.3.4. Потоки ввода/вывода
- •2.1. Основные аспекты операционных систем
- •2.1.1. Функции операционной системы
- •2.1.2. Режимы обработки
1.2.4. Предикаты над процессами
Наряду с сетями и термами агентов множества процессов могут быть охарактеризованы через задание свойств с помощью выражений логики предикатов. Мы будем обсуждать лишь очень простые предикаты. Пусть задан процесс р = (Ео, <о, а); с помощью терма
#(а, Р)
обозначим число событий в р, помеченных действием а. Точно #(а, р) определяется следующей формулой:
#(а, р) = |{ е 6 Е0: сс(е) = а }|.
Обратим внимание, что ;пя бесконечных процессов значение #(а, р) может быть бесконечным. С помощью этой формулы можно образовывать предикаты и тем самым описывать множества процессов.
Пример (множества процессов через предикаты). Рассмотрим следующее множество А действий:
А = {а, Ь, с, d}.
Множество конечных процессов р = (Ео, <о, а) можно охарактеризовать через предикат Q(p). Пусть Q(p) задан с помощью следующих формул:
0 < #(а, р) - #(с, р) < 1 л
0 < #(Ъ, р) - #(d, р) < 1 л
V е, е' е Ео: а(е) = с л а(е') = d => (е <о е' v е' <о е).
Выражаясь словами, имеет место: процесс р выполняет предикат Q, если:
(1) число событий, помеченных через а, либо на единицу больше числа событий, помеченных через с, либо равно ему;
число событий, помеченных через Ь, либо на единицу больше числа событий, помеченных через d, либо равно ему;
события, помеченные через end, не протекают параллельно. □
Часто мы требуем для системы, чтобы ее процессы выполняли определенные инварианты. С инвариантами мы уже познакомились в связи с while-программами в части I. Для процесса р предикат Q называется инвариантом, если для всех (конечных) процессов pj справедлива следующая формула:
Pi Q Р => Q(Pi) -
Инварианты в известной степени характеризуют определенные свойства всех достижимых состояний в системе. Они особенно полезны для харак- теризации свойств бесконечных процессов.
Пример (инварианты бесконечного процесса). Каждый процесс агента
((х ;: а; с; х) || (у :: b; d; у ) ) ||(с. d) 2 :: ( (с; г) or (d; z))
имеет предикат Q из предыдущего примера в качестве инварианта.
Существует ряд свойств процессов Q, которые всегда являются инвариантами, если они относятся только к заданному процессу. Только для этих предикатов Q справедливо следующее высказывание:
Q(P) лр|ср=> Q(Pi). Примером инварианта является взаимное исключение действий а и Ь:
е, d е Е«: а(е) = а л a(d) = b (е <0 d v d <0 е).
Другой пример представляет простая причинность между действиями а и с. Следующий предикат выражает, что действие с имеет место только тогда, когда перед этим имело место действие а:
е е Ео: а(е) = с => В ej е Е0: C| <0 е л a(ej) = а.
Пусть а - некоторое действие. Примером предиката, который никогда не яатяется инвариантом, является предикат Q, задаваемый следующей формулой:
0(р) а#(а, Р) = 1.
Важной задачей в системном анализе при описании процессов сетям.) илп агентами яатяется умение доказать, что все описываемые таким способом (совершенные) процессы удоадетворяют определенным предикатам.
Обратим внимание, что сети Петри (точнее, сети ячеек и вентиле и) можно, например, толковать как графический, сокращенный способ 3.1-
писи для определенных предикатов над процессами. Пусть s - ячейка в сети Петри с множеством Т входных вентилей и множеством Y выходных вентилей. Рис. 1.33 показывает этот вырез сети. При начальной конкретизации b(s) этому вырезу из сети Петри соответствуют следующие инварианты для хода работы р сети:
I {#(а, р): а е Т'} < b(s) + I {#(а, р): а е Т}.
Коньюнкппя по всем этим инвариантам для каждой ячейки дает в итоге инвариант, который однозначно характеризует множество ходов работы сети.
т
Рис.
1.33. Вырез
из сети Петри, который показывает
ячейку р, множество ее входных вентилей
Т и множество выходных ее вентилей Т
г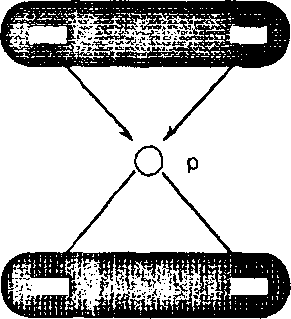
Свойства процессов, описываемые через предикаты, можно разделить на
следующие два класса:
свойства надежности (англ. safety properties) устанавливают, что определенные нежелательные образцы действий в ходе работы системы не встретятся и могут быть заданы через инварианты;
свойства живучести (англ. liveness properties) гарантируют, что определенные желаемые образцы действий в конце концов встретятся в ходе работы системы. Как правило, предикаты для процессов пред- ставыют смесь из свойств надежности и живучести.
Пример (надежность и живучесть). Классическими свойствами надежности являются, например, следующие:
действие а и действие b не имеют места параллельно,
действие а имеет место только после действия Ь
.
Классическим свойством живучести является, например, следующее: • после действия а (точнее, после события, помеченного а) всегда еле- одет по причинной связи определенное действие b. D
Высказывания живучести для процессов могут быть определены по следующей схеме. Для заданных предикатов Q и R, описывающих множества процессов, определим предикат
IQ leads_to R1,
который для процесса р выполняется, если справедлива следующая формула:
V pj: pi с р л Q(p,) => 3 р2: р|ср2срл R(p2).
Пример для такого предиката задается следующей формулой:
|#(а, р) = n leads_to #(а, р) = п + 1|.
С полюшью этой формулы утверждается, что процесс р содержит бесконечно много событий, помеченных действием а.
Высказывания надежности относятся в связи с сетями Петри или агентами всегда к любым, возможно несовершенным, ходам работы, а условия живучести относятся к совершенным ходам работы.
Обратим внимание, что как для сетей Петри, так и для агешов справедливо, что каждый ход работы есть префикс совершенного хода работы,
