3.2.5. Расчет зубчатой передачи

Проектировочный расчет.

Основной задачей является назначение материалов и расчет напряжений.

Принимаем для изготовления шестерни и колеса Сталь 45 с термообработкой – улучшение.

Обоснование: зубья нарезают после термообработки заготовки. При этом достигается достаточная твердость изготовления зубчатых колес без использования дорогих финишных операций. Колеса хорошо прирабатываются.

По справочнику выбираем данные для расчета:

• для шестерни: твердость поверхности зубьев Н₁=269-302 НВ (наиболее вероятная твердость 285 НВ); σ_В1=890 МПа; σ_Т1=650 МПа;

• для колеса: твердость поверхности зубьев Н₂=235-262НВ (наиболее вероятная твердость 250НВ); σ_В2=780 МПа; σ_Т2=6540 МПа.

Определяем допускаемые контактные напряжения:

где σ_Hlimb – предел контактной выносливости;

S_H – коэффициент безопасности;

K_HL – коэффициент долговечности;

Z_R – коэффициент, учитывающий шероховатость сопряженных поверхностей;

Z_V – Коэффициент, учитывающий влияние окружной скорости;

K_L – коэффициент, учитывающий влияние смазки;

K_XH – коэффициент, учитывающий влияние размера колеса.

Потзуясь справочником, принимаем:

• для шестерни:

;

МПа.

S_H=1,1; К_HL=1; Z_R=1; Z_V=1; K_L=1; K_XH=1.

МПа.

• для колеса:

;

МПа.

S_H=1,1; К_HL=1; Z_R=1; Z_V=1; K_L=1; K_XH=1.

МПа.

За расчетное допускаемое контактное напряжение для прямозубой цилиндрической передачи принимаем меньшее из [σ]_H1 и [σ]_H2 - [σ]_рас=518 МПа.

Назначаем коэффициенты. Принимаем коэффициент ширины зубчатого колеса ψ_ba=0,315, К_Нβ=1,15 при b₂/d₁=0,945 и условии, что колеса прирабатываются и находятся вблизи одной из опор; а для прямых зубьев принимаем К_Нα=1, K_HV=1,2.

Определяем межосевое расстояние:

,

где К_ар – средний суммарный коэффициент, равным 9,75 10³МПа^1/3;

К_Нβ - коэффициент распределения нагрузки по ширине колеса;

К_Нα- коэффициент, учитывающий распределение нагрузки между зубьями;

K_HV - коэффициент динамического нагружения зубьев;

ψ_ba - коэффициент ширины зубчатого колеса.

мм.

Принимаем стандартное значение а=1000 мм.

Назначаем модуль:

;

мм.

Принимаем модуль из ряда стандартных значений равный 10. Для силовых передач рекомендуется принимать модуль из условия обеспечения повышения плавности работы передачи.

;

- целое число.

Назначаем числа зубьев:

;

;

;

;

Определяем фактическое передаточное число:

;

.

Определяем процент ошибки, который не должен превышать 5%:

;

.

Рассчитываем геометрические размеры зубчатых колес:

;

мм.

Принимаем из ряда нормальных линейных размеров b₂=320 мм.

;

 мм;

;

мм;

;

мм;

;

мм;

;

мм;

;

мм.

Проверка: ;

мм.

Назначаем степень точности.

Одним из основных показателей качества зубчатых колес является их точность. Точность изготовления зубчатых колес и передач означает не только их кинематические и эксплуатационные показатели, а и такие характеристики как интенсивность шума и вибрации, а также существенно влияет на показатели прочности передачи, долговечность ее работы, потери на трение и т. д.

По нормам кинематической точности, плавности работы и контакта зубьев зубчатые передачи делят на 12 ступеней точности. Основанием для назначения степени точности зубчатых колес рассчитываемой передачи является окружная скорость.

Определяем окружную скорость: ,

м/с.

В соответствии с ГОСТ 1643-81назначаем 9 степень точности.

Проверочный расчет.

Преследует цель проверить работоспособность передачи по все возможным критериям работоспособности. Неудовлетворительные результаты хотя бы одной проверки требуют изменение параметров передачи.

Проверяем на контактную усталостную прочность:

, где Z_M=275 МПа^½ – коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес; Z_ε – коэффициент, учитывающий суммарную длину контактных линий . Здесь ε_α – торцевой коэффициент перекрытия:

;

,

Z_H – коэффициент учитывающий форму сопряженных поверхностей зубьев, для прямозубой передачи принимаем равным 1,77;

;

МПа

Расчетным условие является: : 468,1 МПа<570 МПа – контактная усталостная прочность обеспечена.

Проверяем на усталостную изгибную прочность.

Изгибная прочность зубьев шестерни и колеса в общем случае разная, поэтому для дальнейшего расчета необходимо установить «слабый» элемент.

«Слабым», подлежащим дальнейшему проверочному расчету, зубчатым колесом пары будет то, у которого меньше отношение: .

Определяем допускаемое изгибное напряжение:

,

где σ_Flimb – предел выносливости зубьев при изгибе;

S_H – коэффициент запаса;

K_FC – коэффициент, учитывающий направление приложения нагрузки к зубьям;

K_FL – коэффициент долговечности.

Пользуясь справочником принимаем:

• для шестерни: ; МПа, K_FC=1, K_FL =1, S_H=2,2.

МПа.

• для колеса принимаем K_FC=1, K_FL =1, S_H=2,2, , 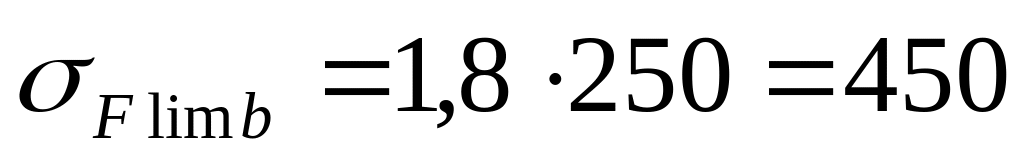МПа.

МПа.

• при Z₁=40 и Z₂=100 и более Y_F1=3,7 и Y_F2=3,6.

;

.

Более «слабым» элементом является колесо, по которому ведется дальнейший расчет.

Расчетным условие является: .

;

.

Изгибная усталостная прочность обеспечена 24,5 МПа<205 МПа.

Проверяем на контактную прочность при действии максимальных нагрузок. Определяем максимальное контактное напряжение: , где К_пер – коэффициент перегрузки

;

;

МПа.

Расчетным условие является:

МПа

Контактная прочность при действии максимальных нагрузок обеспечена – 680МПа<1512 МПа

Проверяем на изгибную прочность при действии максимальных нагрузок. Определяем максимальное изгибное напряжение:

;

МПа;

;

МПа.

Расчетным условие является: : 51,7 МПа<688 МПа – изгибная прочность при действии максимальных нагрузок обеспечена.

Результаты расчетов обеих передач заносим в таблицу.

Таблица 3.3

Результаты расчетов

Параметры	Червяк	Червячное колесо	Шестерня	Зубчатое колесо
Межосевое расстояние	500 мм		1000 мм
d, мм	200	800	330	1670
dα, мм	232	832	350	1690
df, мм	161,6	793,6	305	1645
dω, мм	200	800	-	-
dam, мм	-	864	-	-
b, мм	248	174	325	320