Уравнения теплового баланса при нагревании, испарении, охлаждении и конденсации
НАГРЕВАНИЕ – процесс повышения температуры материалов за счёт подвода к ним теплоты.
Нагревание продукта водой:
,
(3.8)
где индексом 1, 2 обозначены приходящие и уходящие потоки вещества.
При нагревании жидкости насыщенным паром теплота от конденсирующегося насыщенного водяного пара к холодному теплоносителю передаётся через разделяющую их стенку:
.
(3.9)
Греющий “глухой” пар (Dп, iп – массовый расход и энтальпия пара) конденсируется и выводится из теплообменника в виде конденсата (Dп, iп – то же для конденсата).
При нагревании “острым” паром водяной пар вводится непосредственно в нагреваемую жидкость.
.
(3.10)
Пар конденсируется и отдаёт теплоту нагреваемой жидкости, а конденсат смешивается с жидкостью.
При нагревании электрическим током теплота QН выделяется при прохождении электрического тока по нагревательному элементу (ТЭН):
.
(3.11)
ИСПАРЕНИЕ – процесс превращения жидкости в пар путём подвода к ней теплоты.
Расход теплоты на
испарение:
,
(3.12)
где W – масса испаренной жидкости, кг; r – теплота парообразования, кДж/кг.
КОНДЕНСАЦИЯ – переход вещества из паро- или газообразного состояния в жидкое путём отвода из него теплоты:
Количество теплоты, выделяемое при конденсации:
,
(3.13)
где D – масса конденсирующегося пара, кг; r – теплота конденсации, кДж/кг.
Математическая модель процесса конденсации перегретого пара водой (3.14):
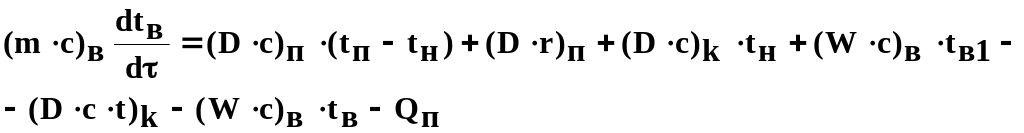
где tн, tk – температура: насыщения (конденсации), конденсата на выходе из аппарата.
ОХЛАЖДЕНИЕ – процесс понижения температуры материалов путём отвода от них теплоты.
Охлаждение теплоносителя водой (3.15):
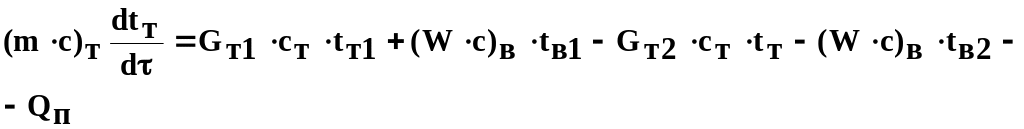
Раздел 3. Типовые модели технологических процессов
1 Пример. Электрическая цепь.
Za
Zb
Uвых
Uвх
Рисунок 4.1. Расчётная схема электрической цепи.
.
Объекты с сосредоточенными параметрами
2 Пример. Регулирование уровня.
2 а. Объект с самовыравниванием.
Qв
H
d
Рисунок 4.2. Схема
модели
управления
уровнем.
,
где Н0 – начальный уровень жидкости в ёмкости.
2 б. Объект без самовыравнивания.
Если расходы на притоке и стоке из резервуара не зависят от уровня жидкости в резервуаре, то такой объект можно рассматривать как чисто накопительный, или интегрирующий элемент. Пусть G1 и G2 – расходы на притоке и стоке соответственно, тогда дифференциальное уравнение объекта имеет вид:
,
(4.1)
линеаризуя и выполнив преобразования Лапласа, получим:
.
Реакцией объекта на ступенчатое изменение расхода ∆G1 и ∆G2 является изменение уровня ∆Н с постоянной скоростью (уровень никогда не достигнет установившегося значения, пока резервуар не переполнится или не опустеет ):
,
.