
- •1.Означення подвійного інтеграла.
- •Таким чином, за означенням 1
- •3.Обчислення подвійного інтеграла у полярних координатах.
- •5.Потрійний інтеграл
- •7.Обчислення потрійного інтеграла у циліндричних координатах.
- •9.Криволінійний інтеграл по довжині дуги (I роду).
- •11.Поняття криволінійного інтеграла другого роду .
- •13.Формула Гріна.
- •15.Означення та властивості поверхневого інтеграла I роду.
- •17.Фізичний зміст поверхневого інтеграла II роду.
- •19. Формула Остроградського – Гаусса. Формула Стокса.
- •2. Обчислення подвійного інтеграла у декартових координатах.
- •4. Застосування подвійних інтегралів.
- •6. Обчислення потрійного інтеграла в декартових координатах.
- •8. Геометричні застосування подвійних інтегралів.
- •10. Застосування криволінійних інтегралів першого роду.
- •12. Застосування криволінійних інтегралів другого роду.
- •14. Умови незалежності криволінійного інтеграла від форми шляху інтегрування.
- •16. Застосування поверхневих інтегралів першого роду.
- •18. Обчислення поверхневого інтеграла другого роду.
19. Формула Остроградського – Гаусса. Формула Стокса.
Формула Остроградського – Гаусса встановлює зв’язок між поверхневим інтегралом по замкненій поверхні і потрійним інтегралом по просторовій області, обмеженій цією поверхнею.
Якщо функції
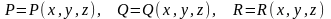 неперервні разом із своїми частинними
похідними першого порядку в замкненої
області G простору, яка обмежена
замкненою гладкою поверхнею σ, то
справедлива формула Остроградського
– Гаусса:
неперервні разом із своїми частинними
похідними першого порядку в замкненої
області G простору, яка обмежена
замкненою гладкою поверхнею σ, то
справедлива формула Остроградського
– Гаусса:
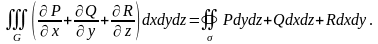 (2.14)
(2.14)
Зауваження 1. На практиці формулу Остроградського – Гаусса можна застосовувати для обчислення об’ємів тіл, якщо відома поверхня, яка обмежує це тіло.
Зауваження 2. Якщо σ – замкнена кусково
– гладка поверхня, одиничний вектор
зовнішньої нормалі якої
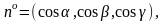 тоді потік П вектора
тоді потік П вектора
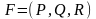 через
поверхню σ можна обчислити за формулою
Остроградського – Гаусса:
через
поверхню σ можна обчислити за формулою
Остроградського – Гаусса:
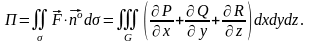 (2.15)
(2.15)
Зауваження 3. Також мають місце формули:
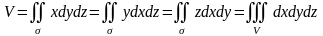 (2.16)
(2.16)
Формула Стокса встановлює зв’язок між поверхневим і криволінійним інтегралами.
Якщо функції неперервні разом із своїми частинними похідними першого порядку на поверхні σ і L – замкнений контур, який обмежує цю поверхню, то справедлива формула Стокса:
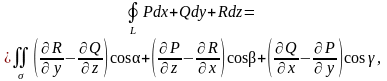 (2.17)
(2.17)
де cos α, cos 𝛽, cos γ – напрямні косинуси нормалі до поверхні σ; напрям нормалі обирається так, щоб із сторони нормалі обхід контуру L відбувався проти годинникової стрілки.
Формулу Стокса можна записати в наступному вигляді:
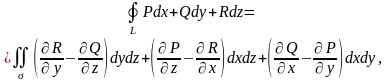 (2.18)
(2.18)
2. Обчислення подвійного інтеграла у декартових координатах.
Теорема 2. Нехай функція
неперервна в області D, обмеженій лініями
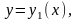
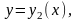
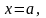
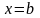 ,
причому функції
,
причому функції
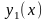 і
і
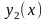 неперервні на відрізку [a; b]
і
неперервні на відрізку [a; b]
і
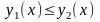 для довільного
для довільного
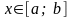 .
Тоді має місце формула
.
Тоді має місце формула
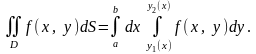 (7)
(7)
Формула (7) показує, що обчислення подвійного інтеграла зводиться до обчислення двох визначених інтегралів. Інтеграл справа у формулі (7) називається повторним, причому інтеграл по змінній y називається внутрішнім, а по змінній x - зовнішнім.
Аналітичне доведення формули (7) дещо громіздке, тому наведемо тут міркування, що випливають з фізичного змісту подвійного інтеграла. Будемо вважати, що функція невід’ємна в області D і є поверхневою густиною пластинки D.
В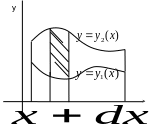 иділимо
смугу області D між вертикалями x
і
иділимо
смугу області D між вертикалями x
і
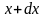 (рис. 3). маса
цієї смуги (вона заштрихована на рис.7.3),
очевидно, дорівнює
(рис. 3). маса
цієї смуги (вона заштрихована на рис.7.3),
очевидно, дорівнює
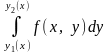 .
Тоді маса всієї пластинки D буде
дорівнювати
.
Тоді маса всієї пластинки D буде
дорівнювати
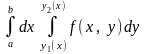 ,
звідки за фізичним змістом подвійного
інтеграла і випливає формула (7).
,
звідки за фізичним змістом подвійного
інтеграла і випливає формула (7).
Приклад 1. Обчислити
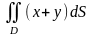 ,
якщо область D обмежена лініями
,
якщо область D обмежена лініями
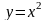 і
і
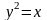 (рис.
4).
(рис.
4).
Розв’язання. Задані лінії перетинаються в двох точках: O(0, 0) і A(1, 1). Тому за формулою (7) маємо:
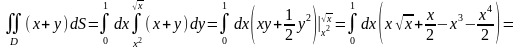

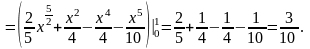
У випадку області D, обмеженої лініями
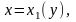
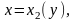
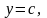
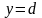 ,
причому функції
,
причому функції
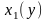 і
і
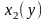 неперервні на відрізку [c; d] і
неперервні на відрізку [c; d] і
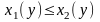 для довільного
для довільного
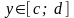 (рис. 5), має місце формула
(рис. 5), має місце формула
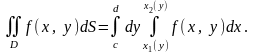 (8)
(8)
Приклад 2. Обчислити
,
якщо область D обмежена лініями
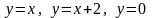 (рис. 6).
(рис. 6).
Розв’язання. З умов прикладу маємо:
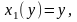
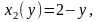
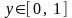 .
Тому за формулою (8)
.
Тому за формулою (8)
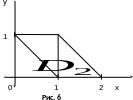
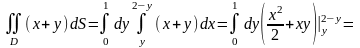
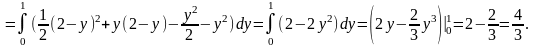
Зауважимо, що даний інтеграл можна
обчислити і за формулою якщо помітити,
що
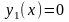 ,
а
,
а
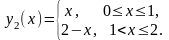
Тоді
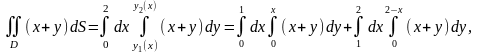
тобто даний інтеграл за адитивною властивістю дорівнює сумі двох інтегралів. Обчислимо кожний з них окремо:
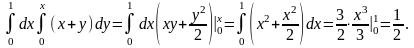
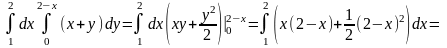
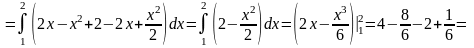
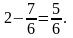
Тоді
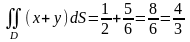 ,
тобто отримали попередній результат,
але обчислень довелося виконати більше,
ніж за формулою (8).
,
тобто отримали попередній результат,
але обчислень довелося виконати більше,
ніж за формулою (8).
