1.Означення подвійного інтеграла.

Нехай у обмеженій квадровній області D задана функція 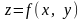. Сіткою (T) кривих довільно розіб’ємо область D на квадровні частини 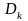, 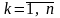. Позначимо

, , .

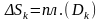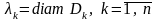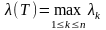У кожній частині довільно візьмемо по одній точці 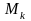, і складемо суму

(3)

яку називають інтегральною. Вона залежить від (T) - розбиття області D на частини і від вибору точок .

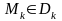Означення 1. Число I називається границею інтегральних сум (3) при 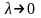, якщо для довільного числа 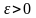існує таке число 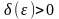, що для довільного (T) - розбиття області D на частини , і довільного вибору точок , , з умови 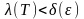випливає нерівність .

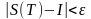При цьому число I називають подвійним інтегралом функції 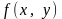по області D і позначають символом 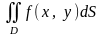або .

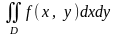Таким чином, за означенням 1

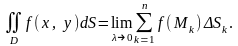(4)

Якщо означення 1 зіставити із задачею про масу неоднорідної пластинки, то отримаємо формулу

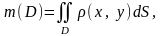(5)

яка розкриває фізичний зміст подвійного інтеграла.

якщо означення 1 зіставити із задачею про об’єм циліндричного тіла, то отримаємо формулу

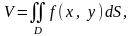(6)

яка розкриває геометричний зміст подвійного інтеграла.

Теорема 1. Якщо функція неперервна в обмеженій квадровній області D, то подвійний інтеграл існує.

Теорему 1 приймаємо без доведення.

Властивості подвійного інтеграла

Основні властивості подвійного інтеграла аналогічні властивостям визначеного інтеграла:

1º.

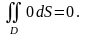
2º.

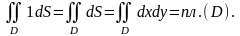
3º.

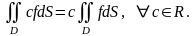
4º.

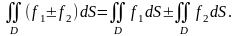
5º. Якщо 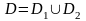і област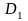і і 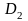не мають спільних внутрішніх точок (вони мають лише спільну межу), то 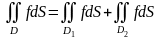(адитивна властивість ).

6º. Якщо функція неперервна в області D, то існує точка 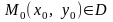така, що 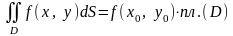(теорема про середнє значення).

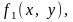
В рівностях 3º, 4º, 5º вважають, що подвійні інтеграли функцій , 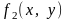по вказаних областях існують.

Доведемо, наприклад, властивість 3º. Маємо

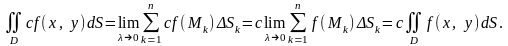
При доведенні використані означення подвійного інтеграла і той факт, що сталий множник можна виносити за знак суми і за знак границі.

З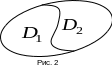 властивості 3º при 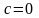отримуємо рівність 1º, а при 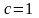і 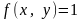в (D) отримуємо рівність 2º.

Рівність 5º, виходячи з фізичного змісту подвійного інтеграла означає наступне: якщо пластинка D є об’єднанням пластинок і (рис. 2), то, очевидно, маса пластинки D дорівнює сумі мас пластинок і .

Теорему про середнє значення приймаємо без доведення.

3.Обчислення подвійного інтеграла у полярних координатах.

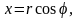
У ряді випадків обчислення подвійного інтеграла спрощується, якщо перейти до полярних координат за формулами 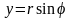. Тоді

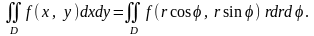(9)

Ф ормулу (9) одержуємо із означення подвійного інтеграла, якщо область D розбити на частини променями 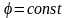і колами 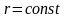. Тоді 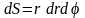(рис. 7).

Приклад 3. Обчислити 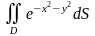, якщо область D обмежена колом радіуса R.

Розв’язання. Використаємо формулу (9) для обчислення даного подвійного інтеграла. маємо:

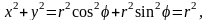
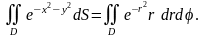
Щоб описати круг 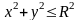, необхідно, щоб r змінювався у межах 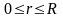, а 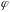- у межах 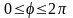. Тому

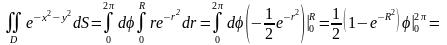
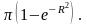
Зауважимо, що в декартових координатах даний інтеграл не можна обчислити за формулами (7) або (8), оскільки первісна функції 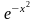не виражається у скінченному вигляді.

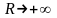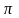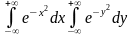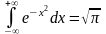Цікаво відзначити, що при даний інтеграл має границю , а область D охоплює всю площину XOY. Запишемо інтеграл у вигляді . Тоді отримаємо, що . Цей результат можна одержати і іншими способами, наприклад за допомогою гама-функції Ейлера.