9.3 Предельная гибкость. Классификация стержней работающих на сжатие.

Установим границы применимости формулы Эйлера. Очевидно, что она применима, если критические напряжения не превышают предел пропорциональности σ_пц т.е. с учётом (9.12)

σ_пц > π²E /λ² или σ_пц = π²E /λ_пр²,

откуда предельная гибкость стержня

λ_пр= ( π²E/ σ_пц)^0.5 (9.15)

Для стержней, гибкость которых больше предельной критическая (Эйлерова) сила и соответствующие напряжения могут быть определены по формулам (9.11, 9.12). Эти стержни будем называть гибкими стержнями. Например, положив для низкоуглеродистой конструкционной стали σ_пц=200МПа и Е=2∙10⁵МПа из (9.15) получим

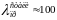
Для стержней, гибкость которых меньше предельной использование формул (9.11, 9.12) даёт существенно завышенные значения критических сил, т.е. ошибку в опасную сторону.

Стержни, теряющие устойчивость при напряжениях близких и больших чем предел текучести σ_кр ≥ σ_т называются жесткими стержнями. У жестких стержней из низкоуглеродистой конструкционной стали λ < 40.

9.4 Устойчивость стержней конечной гибкости

Задача определения напряженно-деформированного состояния стержней из нелинейно упруго-пластического материала представляет значительные математические и вычислительные трудности. Потребность в исследовании потери устойчивости стержнями конечной гибкости возникла в период бума строительства железных дорог и мостов середины и конца 19 века. Вышеупомянутые трудности были преодолены инженерами путём проведения систематических экспериментальных исследований ( Т. Карман, Л. Тетмайер, Ф.С. Ясинский). Русский учёный Ясинский на основании проведенных испытаний предложил аппроксимацию результатов полиномом второй с степени

,

σ_кр= a - b λ + c λ² , (9.16)

который получил название формула Ясинского. Для низкоуглеродистой конструкционной стали найдено

a = 310МПа, b = 1,14МПа, c=0. (9.17)

4. Практический расчёт на устойчивость.

Условие устойчивости сжатого стержня σ < σ_кр

Известная неопределённость левой и правой частей этого неравенства перекрываются коэффициентом запаса на устойчивость n_у и условие устойчивости принимает вид σ ≤ [σ]_у, где

[σ]_у= σ_кр / n_у (9.18)

или σ =P/A ≤φ[σ] (9.19)

Здесь φ =[σ]_у / [σ] (9.20)

- так называемый коэффициент изменения основного допускаемого напряжения [σ], являющийся функцией его гибкости λ.

Наиболее надёжны зависимости φ = φ (λ) (9.21) полученные в результате обработки экспериментальных данных, приводимые в справочной и учебной литературе.

В лекции 10 дана классификация центрально сжатых стержней, подробно рассмотрена процедура проверочного и проектировочного расчётов, а также таблицы зависимостей (9.21) и аппроксимирующие их формулы для различных материалов.