Контрольные вопросы к лекции 8

1 Что означает свести новую задачу к уже решенной?

2 Разъясните суть понятий внешней и внутренней статической неопределимости.

3 Как обычно выбирается основная система метода сил?

4 Какие требования предъявляются к статически неопределимой основной системе метода сил?

5 Как выбирается основная система метода перемещений?

6 Разъясните смысл коэффициентов и свободных членов системы канонических уравнений метода сил.

7 Разъясните смысл коэффициентов и свободных членов системы канонических уравнений метода перемещений.

Лекция 9

Устойчивость в механике абсолютно твёрдого и в механике деформируемого тела. Критическая сила. Дифференциальное уравнение продольного изгиба стержня. Формула Эйлера и Эйлерова сила. Критические напряжения и Эйлеровы напряжения. Зависимость формы потери устойчивости от закрепления концов стержня, приведенная длина стержня и коэффициент приведения длины. Гибкость стержня, предельная гибкость. Классификация стержней по гибкости. Определение критических напряжений для стержней конечной гибкости, опыты и формула Ясинского. Условие устойчивости и допускаемые напряжения на устойчивость, коэффициент изменения основного допускаемого напряжения. Практический расчет на устойчивость – проверочный и проектировочный.

Цель: Ознакомить курсантов с основами понятиями технической теории расчёта центрально-сжатых стержней, как в пределах, так и за пределами линейной упругости.

Рекомендованная литература: [1 стр. 619-644, 2 стр. 582-609, 3 стр. 560-579, 4 стр. 412-455 ]

9.1 Устойчивость в механике.

Рассмотрим простую систему из двух твердых тел - цилиндрической поверхности и шарика, на который действует сила веса (рис. 9.1).

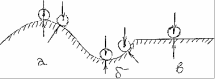
Рис. 9.1 Равновесие простой механической системы твёрдых тел: а) неустойчивое равновесие шарика, б) устойчивое и в) безразличное.

Если сила веса в положении равновесия направлена к центру кривизны поверхности (рис. 9.1а, шарик на «горке»), то при малом отклонении возникнет составляющая реакции Т (см. силовой треугольник), которая стремится увести шарик от неустойчивого положения к новому устойчивому (рис 9.1б, в лунке), где при малом отклонении от положения устойчивого равновесия появляется составляющая стремящаяся вернуть шарик в исходное положение. При нулевой кривизне (плоскость нормальная к силе веса) равновесие – безразличное. Таким образом «жизнь механической системы» (любой) представляет чередование устойчивых и неустойчивых (в относительно большом и малом) положений равновесия, преодолении потенциальных барьеров, скатываний в потенциальные ямы и «прозябаний» в безразличном равновесии.

Механика деформируемого тела содержит меньше ограничений и потому несравненно богаче отражаемыми явлениями. Из возможности изменения формы возникает возможность обнаружения и изучения т. н. устойчивости равновесия формы. Далее ограничимся изучением формы упругого равновесия для наиболее простых элементов конструкций – прямых стержней.