Контрольные вопросы к лекции 5

1 Как понимать статическую неопределимость задачи сопротивления материалов вообще?

2 Разъясните понятия внутренней и внешней статической неопределимости.

3 Поясните общую схему раскрытия статической неопределимости.

4 Суть и последовательность анализа статической неопределимости задач механики деформируемого тела.

5 Три пути синтеза зависимостей, найденных при анализе.

6 Суть метода сил.

7 Суть метода перемещений.

8 Метод сил и условия совместности деформаций.

9 Метод перемещений и условия равновесия.

10 Поясните метод перемещений на простом примере.

11 Поясните метод сил на простом примере.

12 Поясните метод перемещений на простом примере.

13 Что такое основная система в методе сил и в методе перемещений.

14 Запишите в общем виде канонические уравнения метода перемещений, разъясните физический смысл коэффициентов и свободных членов.

15 Запишите в общем виде канонические уравнения метода сил разъясните физический смысл коэффициентов и свободных членов.

16 Поясните сущность и преимущества использования статически неопределимых основных систем в методе сил.

Лекция 6

Сдвиг, основные зависимости, условие прочности. Деформация чистого кручения, условия возникновения. Анализ задачи, основные зависимости. Примеры решения задач на сдвиг и кручение.

Цель: Ознакомить курсантов с простыми деформациями – чистое чистый сдвиг и чистое кручение и, применив метод анализа и синтеза для раскрытия внутренней статической неопределимости, получить рабочие формулы для расчёта бруса на прочность и жесткость.

Рекомендованная литература: [ 1 стр.158-218, 2 стр. 138-156, 196-236, 3 стр.214-255, 4 стр.77-98]

6.1 Чистый сдвиг

Рассмотрим случай плоско напряженного состояния (см. разд. 2.3) изображенный на рис.5.1а при котором главные напряжения σ₁=- σ₃= σ.

Напряжения на гранях расположенных в плоскости чертежа могут быть любыми, в частности σ₂=0 как это имеет место у тонкостенных конструкций.

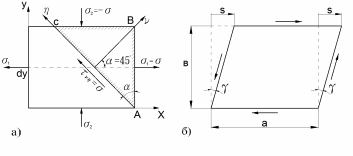
Рис.6.1 а – главные напряжения при чистом сдвиге и напряжения на наклонной площадке;

б – элемент материала ограниченный площадками сдвига и напряжения на нём,

абсолютный сдвиг s и угол сдвига γ.

Плоскостью совпадающей с направлением η и образующей угол α с гранью AB выделим элемент ABC из условия равновесия, которого при α=45^◦ найдём:

σ_ν=0; τ_νη=σ (6.1)

Тот же результат получим для сечений под углом 45^◦ к остальным граням.

Таким образом, элемент материала (рис.5.1б), грани которого (площадки чистого сдвига) повёрнуты на 45^◦по отношению к исходным (рис.5.1а) загружен только касательными напряжениями τ = σ (экстремальными для данного вида напряженного состояния). Величина и направление этих напряжений должны удовлетворять закону парности касательных напряжений

τ_νη= τ_ην , (6.2)

вытекающему из условия равновесия по моментам.

Данный вид напряжённого состояния называется чистый сдвиг. При чистом сдвиге первоначально прямоугольный элемент ограниченный площадками сдвига деформируется в параллелепипед (квадрат - в ромб). Линейное перемещение s (рис.5.1б) носит название абсолютный сдвиг. Угол перекоса γ – угол сдвига. Безразмерное отношение

s/b = tgγ (6.3)

– относительный сдвиг. В силу малости деформаций

tgγ ≈ γ, (6.4)

т.е. относительный сдвиг равен углу сдвига.

При малых деформациях между касательными напряжениями и углом сдвига наблюдается связь близкая к линейной, т.е. имеет место закон Гука при сдвиге:

τ = Gγ, (6.5)

где G носит название модуль сдвига или модуль второго рода.

У изотропных материалов модуль сдвига G, модуль Юнга E и коэффициент Пуассона µ связаны зависимостью (доказательство в Приложении ):

G = . (6.6)

Из (6.6) следует, что из трёх т.н. механических констант изотропного материала E, G и µ независимыми являются только любые две из них. Например, для стали E_ст = 2◦ 10⁵ МПа и µ = 0.3 согласно (6.6) получим G_ст ≈0.8◦ 10⁵МПа. Чистый сдвиг реализуется при чистом кручении цилиндров и призм. По результатам испытания цилиндрических образцов находят предельные касательные напряжения τ_пред соответствующие началу резкого возрастания остаточных деформаций или разрушению образца (в зависимости от требований норм прочности данной области техники).

Условие прочности принимает вид

τ ≤ [τ] , (6.7)

где допускаемые касательные напряжения

[τ]= τ_пред /n. (6.8)

Здесь коэффициент запаса n берётся согласно рекомендациям упомянутых норм прочности.

В определённых сечениях разъёмных и неразъёмных соединений (сварных, заклёпочных, болтовых, шлицевых, шпоночных и др.) напряженно - деформированное состояние близко к чистому сдвигу (срез), поэтому условие (6.7) является одним из условий их прочности. Предельные напряжения в этом случае находят по результатам испытаний или из опыта эксплуатации соответствующих узлов конструкций.